Логическая переменная – это переменная, которая может принимать одно из двух значений ноль и единица (истина или ложь).
Логическая константа – это константа (постоянная величина) которая может принимать значение ноль или единица (истина или ложь).
Логическая функция – это функция, которая может принимать два значения ноль и единица (истина или ложь).
Наиболее универсальным средством представления логической функций может являться таблица истинности.
Таблица истинности – это таблица, показывающая все входные и выходные значения высказывания, процесса, действий и т.д. Приведем простой пример:
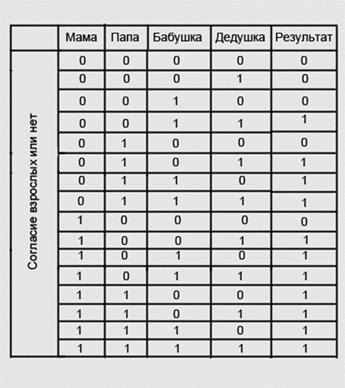 Ребенку очень хочется пойти погулять на улицу. У него есть папа, мама, бабушка и дедушка. Что бы ему разрешили идти гулять необходимо согласие хотя бы двух взрослых. Таким образом, согласие взрослого выразим цифрой “1”, не согласие “0” и построим таблицу истинности.
Ребенку очень хочется пойти погулять на улицу. У него есть папа, мама, бабушка и дедушка. Что бы ему разрешили идти гулять необходимо согласие хотя бы двух взрослых. Таким образом, согласие взрослого выразим цифрой “1”, не согласие “0” и построим таблицу истинности.
Глядя на таблицу истинности видны все варианты исхода событий. Значение результата, где он равен “1” означает, что ребенок пойдет гулять, “0” — не пойдет.
А вот так выглядят таблицы истинности для основных (двоичных) функций.
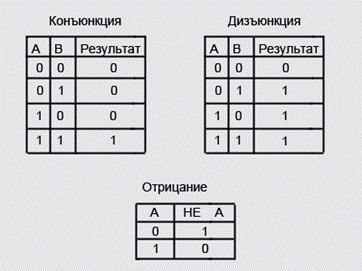
Наиболее широкое применение в алгебре логики получила функционально полная система функций (Булевый базис), выраженная в виде базовых логических функций одной переменной “ НЕ ” (отрицание) и двух функций двух переменных – это “И” (конъюнкция или логическое умножение) и “ИЛИ” (дизъюнкция или логическое сложение).
Элементарные логические функции и их свойства.
Логическая функция - это функция логических переменных, которая
может принимать только два значения: 0 или 1. В свою очередь,
сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения: 0 или 1.
Логический элемент - это устройство, реализующее ту или иную
логическую функцию.
Системаэлементарных логических функций, включающая функции И, ИЛИ и НЕ, называется функционально полной, так как позволяет реализовать любую логическую функцию одним аналитическим выражением.
Двоичные логические операции с цифровыми сигналами (битовые операции)[править | править вики-текст]
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из 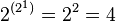 возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ [править | править вики-текст]

Инвертор, НЕ (IEC)
Инвертор, НЕ (ANSI)
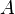
| 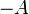
|
Мнемоническое правило для отрицания звучит так: На выходе будет:
· «1» тогда и только тогда, когда на входе «0»,
· «0» тогда и только тогда, когда на входе «1»
Повторение [править | править вики-текст]
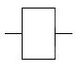
Повторитель (буфер)
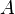
| 
|
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из 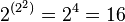 возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция И [править | править вики-текст]

И (IEC)
И (ANSI)
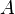
| 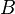
| 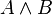
|
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
· «1» тогда и только тогда, когда на всех входах действуют «1»,
· «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Словесно эту операцию можно выразить следующим выражением: "Истина на выходе может быть при истине на входе 1 И истине на входе 2".
Дизъюнкция (логическое сложение). Операция ИЛИ [править | править вики-текст]

ИЛИ (IEC)
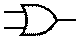
ИЛИ (ANSI)
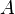
| 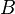
| 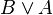
|
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
· «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
· «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера) [править | править вики-текст]

И-НЕ (IEC)
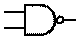
И-НЕ (ANSI)
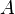
| 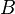
| 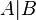
|
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
· «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
· «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса) [править | править вики-текст]
В англоязычной литературе NOR.

ИЛИ-НЕ (IEC)
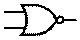
ИЛИ-НЕ (ANSI)
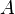
| 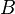
| 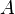 ↓ ↓ 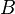
|
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
· «1» тогда и только тогда, когда на всех входах действуют «0»,
· «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ [править | править вики-текст]
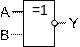
ИСКЛ-ИЛИ-НЕ (IEC)
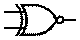
ИСКЛ-ИЛИ-НЕ (ANSI)
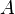
| 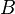
| 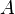 ↔ ↔ 
|
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
· «1» тогда и только тогда, когда на входе действует четное количество,
· «0» тогда и только тогда, когда на входе действует нечетное количество
Словесная запись: "истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2".
Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности. [править | править вики-текст]
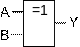
ИСКЛ-ИЛИ (IEC)
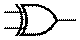
ИСКЛ-ИЛИ (ANSI)
В англоязычной литературе XOR.
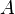
| 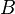
| 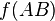
|
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
· «1» тогда и только тогда, когда на входе действует нечётное количество,
· «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: "истина на выходе - только при истине на входе1, либо только при истине на входе 2".
Импликация от A к B (прямая импликация, инверсия декремента, A<=B) [править | править вики-текст]
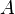
| 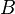
| 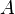 → → 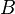
|
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
· «0» тогда и только тогда, когда на «B» меньше «А»,
· «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B) [править | править вики-текст]
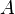
| 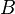
| 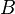 → → 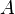
|
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
· «0» тогда и только тогда, когда на «B» больше «А»,
· «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B [править | править вики-текст]
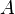
| 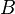
| 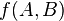
|
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
· «1» тогда и только тогда, когда на «A» больше «B»,
· «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A [править | править вики-текст]
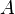
| 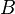
| 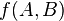
|
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
· «1» тогда и только тогда, когда на «B» больше «A»,
· «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
· И, НЕ (2 элемента)
· ИЛИ, НЕ (2 элемента)
· И-НЕ (1 элемент)
· ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Или (другой вариант)
Функцией (или функциональной зависимостью) называется закон, по которому каждому значению независимой переменной x из некоторого множества чисел, называемого областью определения функции, ставится в соответствие одно вполне определенное значение величины y. Совокупность значений, которые принимает зависимая переменная y, называется областью значений функции.
Графиком функции называется множество всех точек координатной плоскости с координатами (x; y), такими, что абсцисса x принимает все значения из области определения, а ордината y равна значению функции в точке x.
Функция f (x) называется четной, если для любого x из ее области определения, -x также принадлежит области определения, причем, f (-x)= f (x). Функция f (x) называется нечетной, если для любого x из ее области определения, -x также принадлежит области определения, причем, f (-x)= f (x).
Функция f (x) называется периодической с периодом T¹ 0, если для любого x, принадлежащего области определения функции, x - T, x + T также принадлежат области определения и ее значения в точках x, x - T, x + T равны.
Функция f (x) возрастает на некотором интервале, если для любых значений x 1 и x 2, принадлежащих этому интервалу, таких что x 2 > x 1, выполнено неравенство f (x 2) > f (x 1).
Функция f (x) убывает на некотором интервале, если для любых значений x 1 и x 2, принадлежащих этому интервалу, таких что x 2 > x 1, выполнено неравенство f (x 2) < f (x 1).
Точка x 0 называется точкой минимума функции f (x), если для всех значений x из некоторой окрестности x 0 выполнено неравенство bÎ R.
Точка x 0 называется точкой максимума функции f (x), если для всех значений x из некоторой окрестности x 0 выполнено неравенство f (x) £ f (x 0).
При описании функции y = f (x) принято указывать:
1. Область определения D(x) и область значений E(y) функции.
2. Является ли функция периодической.
3. Является ли функция четной или нечетной.
4. Точки пересечения графика с осями координат.
5. Промежутки знакопостоянства функции.
6. Интервалы возрастания и убывания.
7. Точки экстремума и экстремальные значения.
8. Наличие асимптот.
9. График.
Нормальные формы булевых функций
Нормальные формы логических функций Нормальной формой логической функции является такая формула, которая считается наиболее наглядной и удобной в использовании, чем любая другая равносильная ей формула.
Нормальные формы: Дизъюнктивные(совершенные, несовершенные) и конъюнктивные(совершенные, несовершенные).
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.
Формулы в ДНФ:
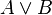
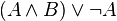
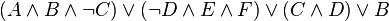
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.[1] Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.
Формулы в КНФ:
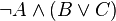
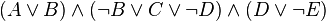
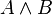
Формулы не в КНФ:
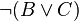
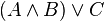
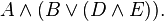
Но эти 3 формулы не в КНФ эквивалентны следующим формулам в КНФ:
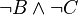
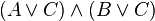
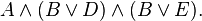
 2015-06-04
2015-06-04 1379
1379






