2015-06-14
1424
Регулярные множества хороши тем, что их можно очень просто описать формулами, которые мы назовем регулярными выражениями.
Определение 2. Класс регулярных выражений над конечным словарем V определяется так:
1. 
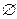и e — регулярные выражения;
2. ("a Î V)а — регулярное выражение;
3. Если R1 и R2 — регулярные выражения, то регулярными выражениями являются:
- их сумма R1+R2;
- их произведение R1R2;
- их итерация R1* и R2*.
4. Если выражение не построено конечным числом применения правил 1—3, то оно не является регулярным.
Знак произведения можно опускать. Для уменьшения числа скобок, как и в любой алгебре, используются приоритеты операций: итерация самая приоритетная; менее приоритетно произведение; самый низкий приоритет у сложения.
Примеры регулярных выражений: ab + bа*; (аа)*b + (с + dab)*.
Очевидно, что регулярные множества и регулярные выражения весьма близки. Но они представляют собой разные сущности: регулярное множество — это множество цепочек (в общем случае бесконечное), а регулярное выражение — это формула, схематично показывающая, как было построено соответствующее ей регулярное множество с помощью перечисленных выше операций (и эта формула конечна).
|
|
|
Пусть R^ — регулярное множество, соответствующее регулярному выражению R. Тогда:
1. Если R = 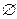, то R^ = .
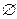2. Если R = e, то R^ = {e}.
3. Если R = а, то R^ = {a}.
4. Если R = R1+R2, то R^ = Rl^ÈR2^.
5. Если R = R1·R2, то R^ = R1^·R2^.
6. Если R = R1*, то R^ = R1^*.
Таким образом, регулярное выражение — это конечная формула, задающая бесконечное множество цепочек, то есть язык.
Рассмотрим примеры регулярных выражений и соответствующих им языков.
| Регулярное выражение | Соответствующий язык | |
| bа* | Все цепочки, начинающиеся с b, за которым следует произвольное число символов а | |
| a*ba*ba* | Все цепочки из а и b, содержащие ровно два вхождения b | |
| (а+bb)* | Все цепочки из а и b, в которые символы b входят только парами | |
| (a+b)*(aa+bb)(a+b)* | Все цепочки из а и b, содержащие хотя бы одну пару рядом стоящих а или b | |
| (0+1)*11001(0+1)* | Все цепочки из 0 и 1, содержащие подцепочку 11001 | |
| a(a+b)*b | Все цепочки из а и b, начинающиеся символом а и заканчивающиеся символом b |
Очевидно, что множество цепочек регулярно тогда и только тогда, когда оно может быть представлено регулярным выражением. Однако одно и то же множество цепочек может быть представлено различными регулярными выражениями, например, множество цепочек, состоящее из символов а и содержащее не менее двух а может быть представлено выражениями: аа*а; а*ааа*; ааа*; а*аа*аа* и т. д.
Определение 3. Два регулярных выражения R1 и R2 называются эквивалентными (обозначается Rl = R2) тогда и только тогда, когда R1^ = R2^.
|
|
|
Таким образом, аа*а = а*ааа* = ааа* = а*аа*аа*. Возникает вопрос, как определить эквивалентность двух регулярных выражений.
Теорема 1. Для любых регулярных выражений R, S и Т справедливо:
1. R+S = S+R; R+R=R; (R+S)+T = R+(S+T); 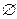+R = R;
2. Re = eR = R; (RS)T = R(ST); 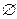R = R 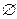= 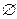; но в общем случае RS ¹ SR;
3. R(S+T) = RS+RT; (S+T)R = SR+TR;
4. R* = e+R+R2+R3+... +RkR*; RR*=R*R; R(SR)* = (RS)*R;
5. R+ = R+R2+R3+...; R*R+ = RR*; R++e = R*.
Эти соотношения можно доказать, проверяя равенство соответствующих множеств цепочек. Их можно использовать для упрощения регулярных выражений. Например: b (b + aa*b) = b (eb + aa*b) = b (e + aa*) b = ba*b. Отсюда b (b + aa*b) = ba*b, что неочевидно.
