1 Вычерчиваем схему нагружения (рисунок 1). Определяем реакции опор и строим эпюры поперечной силы и изгибающего момента.
Направив реакции опор в точке B вверх и в точке E вниз (горизонтальная реакция НB заведомо равна нулю), составим уравнения моментов относительно опоры B
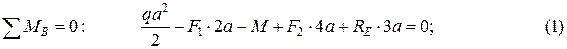
отсюда находим RE:
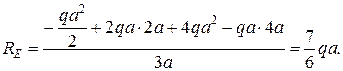
Уравнение моментов относительно опоры E
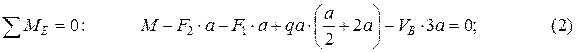
отсюда находим VB:
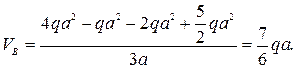
Для проверки составим уравнение проекций всех сил на ось y
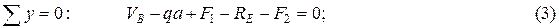
подставляя значения, получим
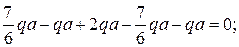
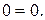
Условие проверки выполняется, значит, проведенные выше вычисления верны.
2 Разбиваем балку на четыре силовых участка BC, CD, ED и AE; для каждого участка применяем метод сечений и составляем уравнения поперечной силы и изгибающего момента. Определяем характерные ординаты поперечной силы и изгибающего момента.
Рассмотрим участок BC:
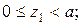

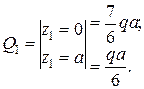
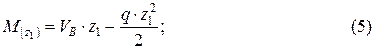
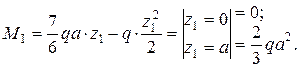
Аналогично рассмотрим участок СD:
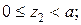

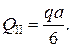
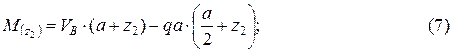
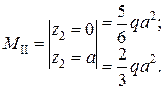
Аналогично рассмотрим участок AE:
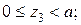

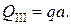

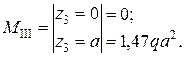
Аналогично рассмотрим участок ED:
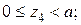

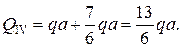
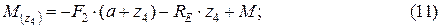
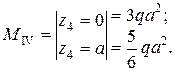
По полученным результатам строим эпюры Q и М (рисунок 1). Эпюра изгибающего момента построена на растянутом волокне.
 |
3 Выполняем проектировочный расчет стальной балки из условия прочности по нормальным напряжениям при изгибе:

отсюда находим расчетный момент сопротивления:

где Миmax – максимальный изгибающий момент, по эпюре моментовполучим 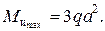
Тогда
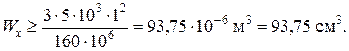
По расчетному моменту сопротивления Wx выполняем подбор сечений стальной балки в следующих вариантах:
а) стальное двутавровое по ГОСТ 8239-72 (рисунок 2); по сортаменту выбираем двутавр № 16, для которого Wx = 109 см3; площадь сечения двутавра A дв = 20,2 см2, осевой момент инерции Ix = 873 см4, статический момент половины сечения Sx = 62,3 см3. Расчетный момент сопротивления меньше табличного значения, следовательно, недогрузка двутаврового сечения составляет
 |
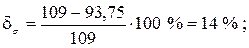
Рисунок 2 – Двутавровое сечение
б ) стальное прямоугольное при 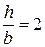 (рисунок 3); на основании зависимости
(рисунок 3); на основании зависимости
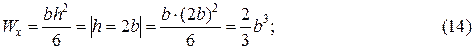
получим сторону основания прямоугольника

или, после подстановки числовых значений
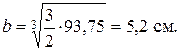
Принимаем b кратное двум, т.е. b = 52 мм, тогда h = 2×52=104 мм.
Площадь прямоугольного сечения
 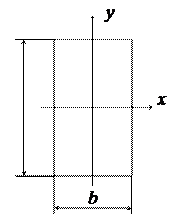 |

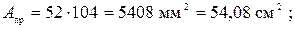
Рисунок 3 – Прямоугольное сечение
в) стальное круглое (рисунок 4); на основании формулы

получим диаметр

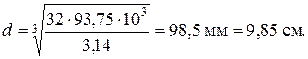
Принимаем, округляя по стандартному ряду, d = 100 мм.
Тогда площадь круглого сечения

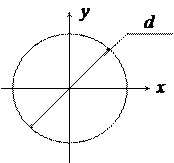 |
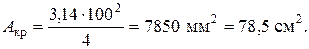
Рисунок 4 – Круглое сечение
Выполняем оценку экономичности сечений стальной балки, сравнивая их веса по соответствующим величинам площадей:
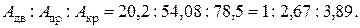
Таким образом, заключаем, что самым целесообразным является двутавровое сечение;
г) чугунное трапециевидное (рисунок 5); предварительно найдем некоторые геометрические характеристики сечения.
Определим площадь сечения:

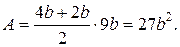
    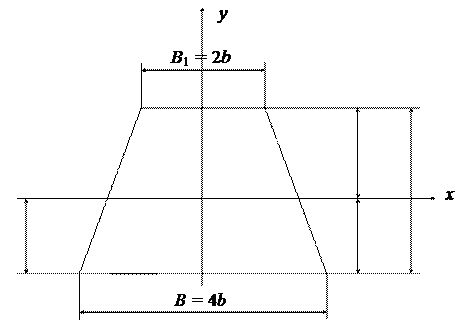 |
Рисунок 5 – Сечение чугунной балки
Координата (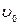 ) - центра тяжести сечения
) - центра тяжести сечения

Подставляя значения, получим
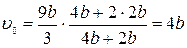 .
.
Осевой момент инерции сечения
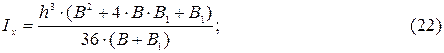
подставляя числовые значения, получим
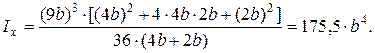
Осевые моменты сопротивления для верхних и нижних точек сечения:

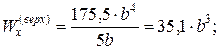

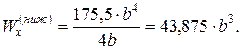
По этим значениям Wx вычислим, во сколько раз напряжения в верхних волокнах больше, чем в нижних.
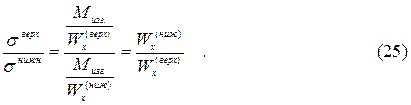
Подставляя значения, получим
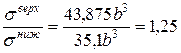 .
.
 |
Рационально расположим поперечное сечение балки. По эпюре М изг (рисунок 1) видим, что в опасном сечении на опоре Е (где
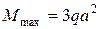 ) растягиваются нижние волокна. Учитывая, что чугун – хрупкий материал, и хуже сопротивляется растяжению, чем сжатию, расположим сечение так, чтобы в нем растягивающие напряжения имели меньшую величину, чем сжимающие, т.е. следующим образом (рисунок 6):
) растягиваются нижние волокна. Учитывая, что чугун – хрупкий материал, и хуже сопротивляется растяжению, чем сжатию, расположим сечение так, чтобы в нем растягивающие напряжения имели меньшую величину, чем сжимающие, т.е. следующим образом (рисунок 6):
Рисунок 6 - Расположение сечения рациональным образом
Проведем подбор сечения их условия прочности по растягивающим напряжениям.
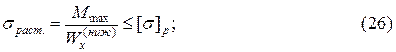
или
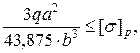
отсюда

Подставляя числовые значения, получим
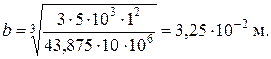
По полученному значению 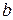 проверим сечение на прочность по сжимающим напряжениям:
проверим сечение на прочность по сжимающим напряжениям:

Подставляя значения, получим
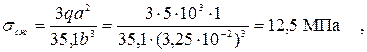
что меньше, чем 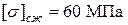 , т.е. прочность балки обеспечивается.
, т.е. прочность балки обеспечивается.
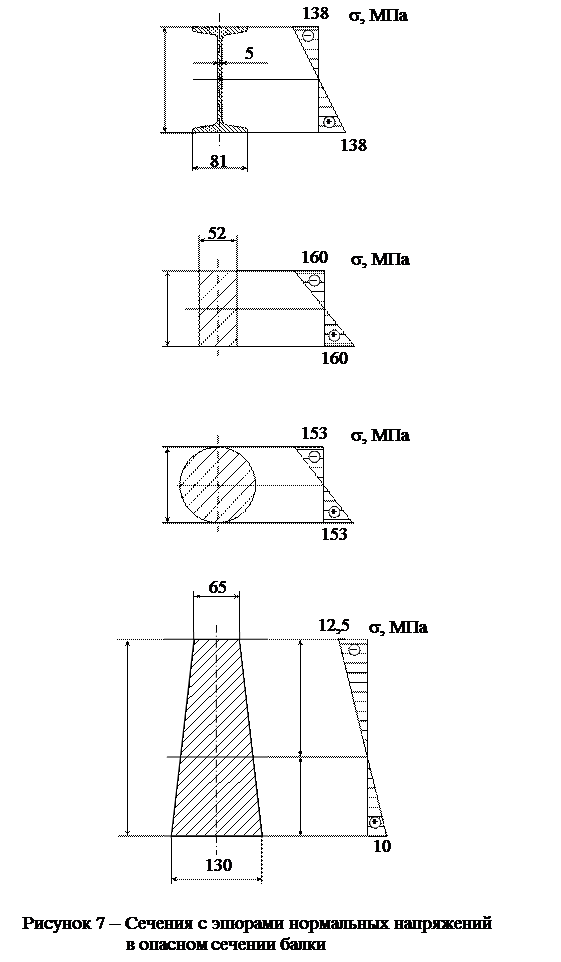
Построим все сечения в одном масштабе с эпюрами нормальных напряжений в опасном сечении балки (рисунок 7), найдя их по формуле

Для стального двутаврового сечения получим:
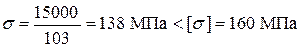 ,
,
при площади 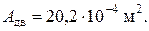
Для стального прямоугольного сечения

подставляя числовые значения, имеем
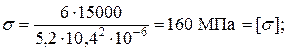
площадь сечения 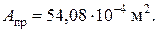
Для стального круглого сечения

подставляя числовые значения, имеем
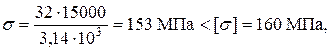
площадь сечения 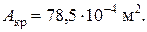
Для трапециевидного сечения имеем
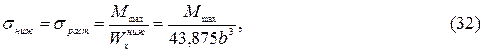
подставляя числовые значения, получим
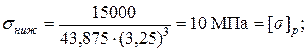
для верхних волокон сечения напряжения, были определены раньше
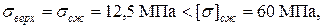
а площадь сечения найдется как
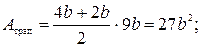
   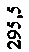 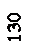 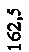  |
или
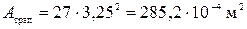 .
.
Анализируя эпюры нормальных напряжений (рисунок 7), видим, что все сечения удовлетворяют условию прочности, но наиболее экономичным является двутавровое сечение, имеющее меньший погонный вес; на что указывает следующее соотношение площадей:
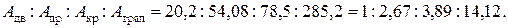
4 Для балки двутаврового профиля проведем полную проверку прочности, выбрав наиболее опасное сечение, где одновременно возникает большой изгибающий момент и поперечная сила:
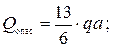
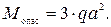
Для полной проверки прочности построим эпюры нормальных (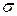 ), касательных (
), касательных (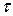 ) и главных (
) и главных (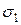 ,
, 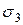 ) напряжений, используя следующие формулы:
) напряжений, используя следующие формулы:



Результаты расчета приводим в табличной форме (таблица 1).
Для двутаврового сечения выбираем из таблицы сортамента
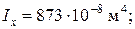
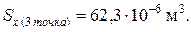
Знак касательных напряжений определяется по знаку 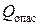 , т.е. будет положительным.
, т.е. будет положительным.
Таблица 1 – Результаты расчета напряжений в точках опасного сечения двутавровой балки
| Точки | si, МПа | yi, см | Siотс, см3 | Аiотс, см2 | YCi, см | b(Y)i, см | ti, МПа | s1i, МПа | s3i, МПа |
| -138,0 | -8 | 8,1 | -138 | ||||||
| -124.1 | -7,22 | 48,73 | 6,32 | 7,71 | 8,1 | 0,98 | 0,002 | -126,1 | |
| 2I | 0,5 | 15,86 | 2,0 | -122,3 | |||||
| 62,3 | 10,1 | 6,17 | 0,5 | 20,28 | 20,28 | -20,28 | |||
| 4I | 124,1 | 7,22 | 48,73 | 6,32 | 7,71 | 0,5 | 15,86 | 126,1 | -2,0 |
| 8,1 | 0,98 | 122,3 | -0,002 | ||||||
| 138,0 | 8,1 |
По полученным значениям строим эпюры нормальных касательных и главных напряжений в опасном сечении балки (рисунок 8).
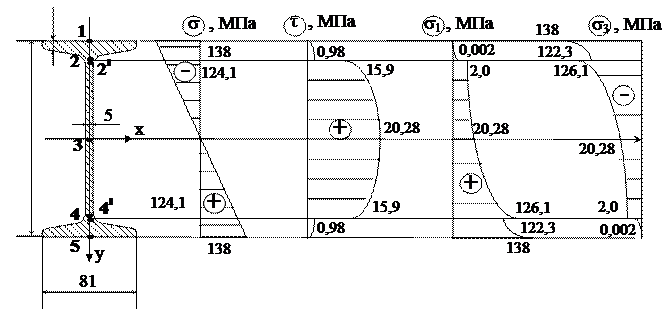
Рисунок 8 – Эпюры напряжений в опасном сечении балки
Для опасной точки 2’, где 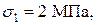
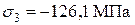 , производим проверку прочности по четвертой теории прочности:
, производим проверку прочности по четвертой теории прочности:
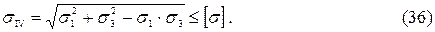
Подставляя числовые значения, получим
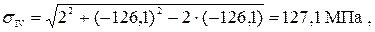
что меньше 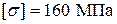 , т.е. условие прочности выполняется.
, т.е. условие прочности выполняется.
Для точки 4’ сечения графически найдем величины главных напряжений при помощи круга Мора (рисунок 9).
Имеем
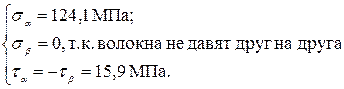 ;
;
Найдя полюс П, определим положение главных площадок и изобразим их на выделенном элементе (рисунок 10).
Сравнивая значения 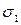 и
и 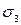 , найденные аналитически и графически, видим, что они практически равны:
, найденные аналитически и графически, видим, что они практически равны:
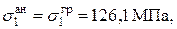
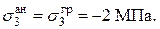
 | |||
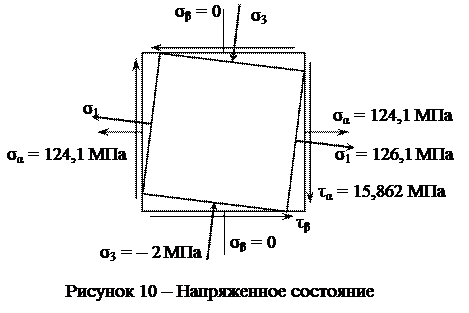 |
 |
5 Пользуясь универсальным уравнением упругой линии балки (УУУЛБ) метода начальных параметров, определим прогиб в сечении «А» и угол поворота в сечении «В» (рисунок 11).
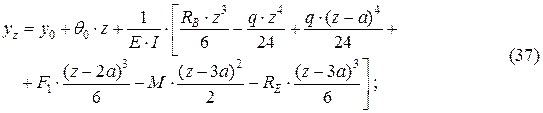
Найдем начальные параметры 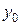 и
и 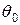 из граничных условий:
из граничных условий:
при z = 0, прогиб на опоре В 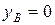 , тогда
, тогда
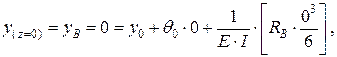
отсюда
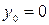 ;
;
при z = 3 a, прогиб на опоре Е 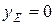 , тогда
, тогда
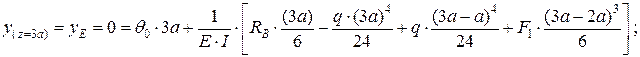
отсюда определим угол поворота в начале координат
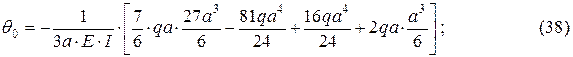
после преобразований имеем
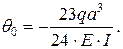
Подставляя числовые значения, получим
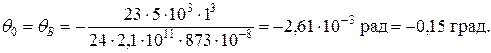
С учетом найденных начальных параметров преобразуем УУУЛБ, т.е. зависимость (37)
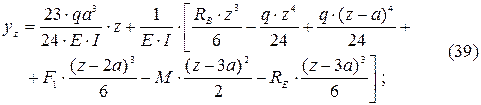
Найдем прогибы в точках С, D, и А (рисунок 12).
Прогиб в точке С
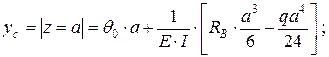
подставляя числовые значения, получим
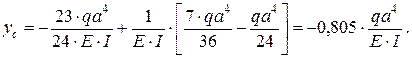
Прогиб в точке D
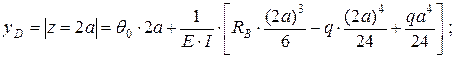
подставляя числовые значения, получим
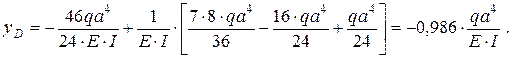
Прогиб в точке A
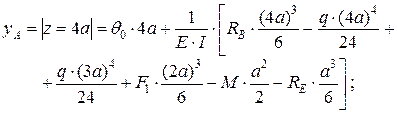
с учетом значений нагрузок, имеем
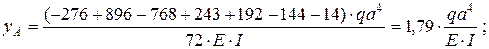
после подстановки числовых величин получим прогиб в сечении А
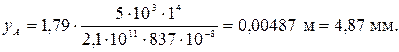


|
|
|


|
|

 По найденным значениям перемещений изобразим упругую линию балки (рисунок 12).
По найденным значениям перемещений изобразим упругую линию балки (рисунок 12).
| |||||
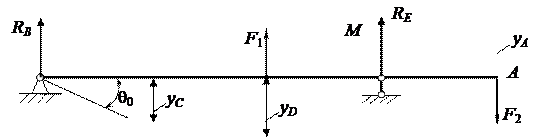 | |||||
|
 2015-06-16
2015-06-16 1605
1605






