2015-06-04
10861
Числовой функцией называется такое соответствие между числовым множеством X и множеством R действующих чисел, при котором каждому числу их множества X сопоставляется единственное из множества R. (Множество X называют областью определения функции. Множество R – это множество действительных чисел.)
Способы задания функций. 1. при помощи уравнения-формулы 2. при помощи таблицы 3. с помощью графика
Экзаменационный билет №16. Функциональные соответствия. Числовые функции, способы их задания. График функции. Примеры числовых функций из начального курса математики.
Функциональным соответствием между множествами X и Y называют такое соответствие, при котором каждому элементу из множества X сопоставляется не более одного элемента из множества Y.
Примеры соответствий, изучаемых в начальном курсе математики.
Примером функциональных соответствий могут служить соответствия, графы которых изображены на рисунке.
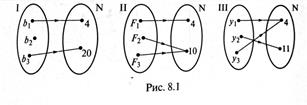
Частным случаем функционального соответствия между множествами X и Y является соответствие, при котором каждому элементу из множества X сопоставляется точно один элемент из множества Y. Такое соответствие называется отображением множества X во множество Y.
Функция - одно из важнейших понятий математики, исходное понятие ведущей ее области - математического анализа. В школьном курсе математики основное внимание уделяется числовым функциям.
Числовой функцией называют такое соответствие между числовым множеством X и множеством R действительных чисел, при котором каждому числу из множества X сопоставляется единственное число из множества R.
Множество X называют областью определения функции.
Функции принято обозначать буквами f,g,h и др. Если f - функция, заданная на множестве X, то действительное число y, соответствующее числу x из множества X, часто обозначают f(x) и пишут y=f(x). Переменную x при этом называют аргументом (или независимой переменной) функции f. Множество чисел вида f(x) для всех x из множества X называют областью значений функции f.
Для задания функции необходимо указать, во-первых, числовое множество X, т.е. область определения функции, и, во-вторых, правило, по которому каждому числу из множества X соответствует единственное действительное число.
Часто функции задают с помощью формул, указывающих, как по данному значению аргумента найти соответствующее значение функции.(y=2x-3, y=x₂, y=3x, где x - действительное число, задают функции, поскольку каждому действительному значению x можно, производя указанные в формуле действия, поставить в соответствие единственное значение y). С помощью одной и той же формулы можно задать как угодно много функций, которые будут отличаться друг от друга областью определения.
Числовые функции можно представлять наглядно на координатной плоскости. Пусть y=f(x) – функция с областью определения X. Тогда ее графиком является множество таких точек координатной плоскости, которые имеют абсциссу x и ординату f(x) для всех x из множества X.
Так, графиком функции y=2x-3, заданной на множестве R, является прямая (рис. 9.1), а графиком функции y=x₂, заданной также на множестве R,- парабола (рис. 9.2).
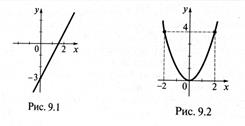
Функции можно задавать с помощью графика. (рис. 9.3 а, б) задают функции, одна из которых имеет в качестве области определения промежуток [-2, 3], а вторая – конечное множество {-2, -1, 0, 1, 2, 3}.
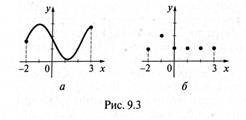
В начальном курсе математики понятие функции и все, что с ним связано, в явном виде не изучается, но идея функциональной зависимости буквально пронизывает его, а правильное понимание таких свойств реальных явлений, как взаимозависимость и изменяемость, является основой научного мировоззрения. Учитель начальных классов должен обладать определенными знаниями о функции и её свойствах.
2. Основные этапы решения текстовой задачи и приемы их выполнения. Иллюстрация приемов на примере решения задачи из начального курса математики (№553 Н.Б.Истомина, 4 класс,2008 г.)
Решение любой задачи - процесс сложной умственной деятельности. Чтобы овладеть им, надо знать основные этапы решения задачи и некоторые приемы их выполнения:
1)анализ задачи; (понять в целом ситуацию, описанную в задаче; выделить условия и требования; назвать известные искомые объекты, выделить все отношения (зависимости) между ними).
2)поиск и составление плана решения задачи; (установить связь между данными и исходными объектами, наметить последовательность действий).
3)осуществление плана решения задачи; (найти ответ на требования задачи, выполнив все действия в соответствии с планом).
4)проверка решения задачи. (установить правильность или ошибочность выполненного решения)
Задача №553
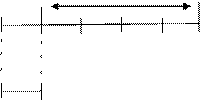200 м.
Дл.
Ш.
Решение:
1) 200:4=50 (м.)- ширина
2) 50+200=250 (м.)- длина
3) 250*50=12500 (м₂)
Ответ: площадь дна бассейна 12500 м₂
17. Прямая и обратная пропорциональности, их свойства и графики. Использование свойств прямой и обратной пропорциональности при решении текстовых задач.
Числовая функция – соответствие между числовым мн-вом Х и мн-вом R, при кот каждому числу из мн-ва Х сопоставляется единств число из мн-ва действит чисел(R). Способы задания ф-ции: формула (по данному значению аргумента найти соответствующее значение функции), график, таблица.
Прямой пропорциональностью наз.ф -ю,к-я может б. задана при помощи формулы y=kx, где k-не равное нулю действит. число. Название ф-и y=kx связано с тем, что в формуле y=kx есть переменные x и y, к-е могут б. значениями величин. А если отношения 2х величин равно некоторому числу, отличному от нуля, их называют прямо пропорциональными. y/x=k(k≠0) –это число коэффициент пропорциональности.
ф-я y=kx- матем. модель многих реальных ситуаций. Если в одном пакете муки 2кг, а куплено х таких пакетов, то всю массу купленной муки обозначим через у можно представить у=2х, т.е зависимость явл. прямой с коэф. k=2.
Св-ва:
1) Областью опред. ф-и y=kx и областью ее значения явл. мно-во действит. чисел.
2) Графиковм прямой пропорц. Явл. прямая, проходящая через начало координат. Достаточно найти лишь одну точку, принадл. Ему и не совпадающую с началом координат, а затем провести прямую.
С увеличением(уменьшением) значения переменной х в несколько раз соответствующее значение переменной у увелич(уменьш) во столько же раз. Присуще только прямой пропорц.Им можно польз-ся при решении задач, в к-х рассматрив. Прямо пропорциональн. величины.
Обратной пропорц. Наз. Ф-ю,кот. Может б. задана формулой у=к/х, где к- не равное нулю действит. число. Название связано с тем, что у у=к/х есть переменные х и у, к-е могут. Б. значениями величн. А если произведение 2х величин равно некоторому числу, отличному от нуля, то их наз. Обратно пропорц. Ху=к(k≠0). Число к-коэфф. Пропорц.
Св-ва:
1) Обл. опред. и областью значений х явл. мно-во действит. числе отличных от нуля.
2) Графиком явл. гипербола
3) При к>0 ветви гиперболы расположены в 1 и 3 четв. И ф-я у=к/х явл убывающей на всей области определения х. При к<0 ветви во 2 и 4 четв. И ф-я явл. возрастающей навсей области опред. х.
С увеличением (уменьш) значения переменной х в несколько раз соответствующее значение переменной у уменьшается(увелич) во столько же раз. Присуще только обр. пропорц. И использ. При решении задач с обратно пропорц. Величинами.
Билет №18. Отношения на множестве, их свойства. Отношения эквивалентности и порядка. Примеры отношений из начального курса математики.
Отношения между элементами одного множества называют отношением на множестве.
Бинарным отношением на множестве Х называется всякое подмножество декартового произведения Х×Х.
xRy – элемент х находится в отношении R с элементом у.
Отношение на конечном множестве Х можно представить наглядно при помощи графа.
R: “x<y” X={2,4,6,8}
Способы задания отношений: перечисление пар, граф, характеристическое свойство пар.
Свойства отношений:
1) Рефлексивность. Отношение R на множестве Х называется рефлексивным, если о любом элементе множества Х можно сказать, что он находится в отношении R с самим собой.
R рефлексивно на ХóxRx, хϵХ
Если отнош рефлексивно, то в каждой вершине его графа есть петля.
2) Симметричность. Отношение R на множестве Х называется симметричным, если из того, что элемент х находится в отношении R с элементом у следует, что и элемент у находится в отношении R с элементом х. R симметрично на ХóxRy => yRx.
На графе все стрелки парные.
3) Антисимметричность. Отношение R на множестве Х называется антисимметричным, если для различных элементов х и у их множества Х, из того, что элемент х находится в отношении R с элементом у следует, что элемент у не находится в отношении R с элементом х. R антисимметрично на Хó х≠у, xRy => yRx
На графе нет парных стрелок.
4) Транзитивность. Отношение R на множестве Х называется транзитивным, если из того, что элемент х находится в отношении R с элементом у, и элемент у находится в отношенииR с элементом z следует, что элемент х находится в отношении R с элементом z.
R транзитивно на ХóxRy и yRz=> xRz.
5) Антирефлексивность. Отношение R на множестве Х называется антирефлексивным, если о любом элементе множества Х можно сказать, что он не находится в отношении R с самим собой.
R антирефлексивно на Хó хϵХ, xRx
6) Связанность. Отношение R на множестве Х называется связанным, если для любых элементов х и у из множества Х, из того, что х≠у следует, что либо х находится в отношении R с элементом у, либо у находится в отношении R с элементом х.
R связанно на Хóх≠у, xRy или yRx
На графе две любые вершины соединены стрелкой.
Отношение R на множестве Х называется отношением эквивалентности, если одновременно обладает свойствами рефлексивности, симметричности и транзитивности.
Рассмотрим на множестве Х отношение равенства дробей. Построим граф этого отношения. Х={2/4, 2/6, 2/8, 6/12, 6/18, 3/6}
По графу мы видим, что данное отношение явл-ся отношением эквивалентности.
Данное отношение обладает одновременно тремя свойствами: рефлексивностью, симметричностью и транзитивностью => отношение R является отношением эквивалентности.
Для отношения эквивалентности выполняется следующее утверждение: Если на множестве Х задано отношение эквивалентности, то оно порождает разбиение множества на попарно непересекающиеся подмножества или классы. Верно и обратное утверждение: Если какое-либо отношение на множестве Х порождает разбиение множества на классы, то это отношение является отношением эквивалентности.
В нашем случае отношение R породило разбиение множества Х на классы равных дробей.
В 1 класс вошли: 2/4, 6/12, 3/6; во 2: 2/6, 6/18; в 3: 6/18
Произошло разбиение множества х на 3 класса равных дробей. Использование приема классификация тесно связано с изучением конкретного материала. Уже на первых уроках детям предлагаются различные предметы по форме, цвету, размеру. Ставится вопрос «Какой предмет лишний?». При этом возможны различные ответы. Или «Разбейте все предметы на несколько групп» (дочисловой период,с.5,с.26).
