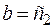Свойства функций, непрерывных на отрезке

Приведем несколько теорем, характеризующих свойства непре­рывных на отрезке функций.

Теорема Вейерштрасса. Если функция непрерывна на отрезке 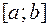, то на этом отрезке она ограничена и достигает своих нижней и верхней граней, т. е. на нем существуют по крайней мере две точк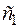и и 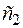, такие, что

, .

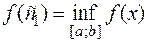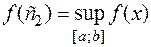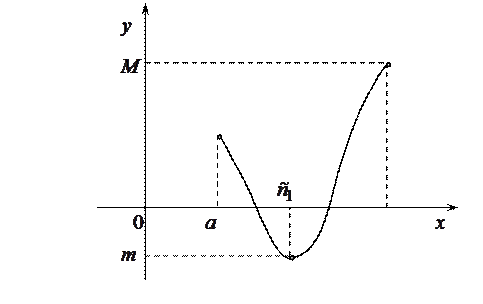
Например, функция 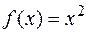непрерывна на отрезке [–2; 3]. Она ограничена на [–2; 3] ( 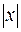b 9) и существуют такие две точк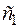и = 0 и 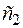= 3, принадлежащие отрезку [– 2; 3], что

, .

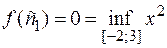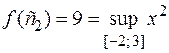Заметим, что непрерывная функция на открытом промежутке ]а; Ь[ может быть неограниченной и, следовательно, не иметь своих точных нижней и верхней граней. Такой функцией является, на­пример, функция 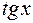на интервале ] ; [.

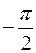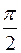Теорема (о сохранении знака). Если функция непрерывна в точке и 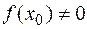, то существует такая окрестность точки , в которой знак функции совпадает со знаком .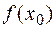

Доказательство этой теоремы основывается на использовании теоремы о плотности числовой прямой. Геометрическая интерпретация этой теоремы дана на рисунках.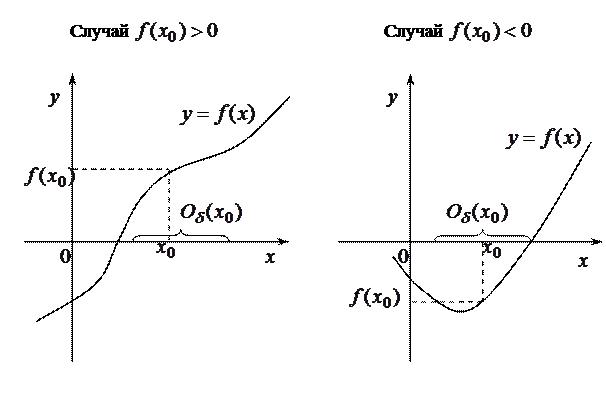

Например, функция 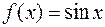непрерывна в точке 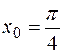, и 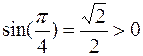.Следовательно существует такая окрестность точки 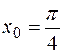, в которой функция 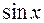сохраняет знак, т. е. .

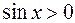Теорема Больцано — Коши. Если функция непрерывна на отрезке 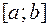и на его концах принимает значения разных знаков, то внутри этого отрезка существует по крайней мере одна точка, в которой значение функции равно нулю.

Геометрический смысл теоремы заключается в следующем: если точк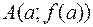и и 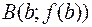графика функции , соответствующие концам отрезка 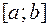, лежат по разные стороны от оси 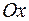, то график функции хотя бы в одной точке отрезка пересекает ось .

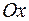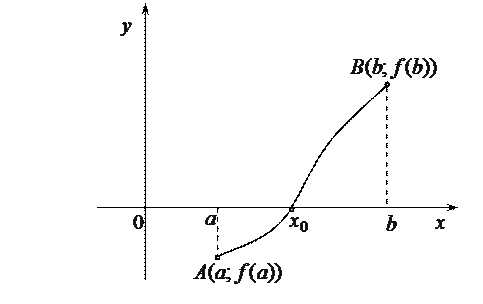
Функция , график которой представлен на рисунке ниже, имеет три точки: 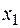, , 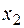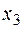где .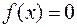

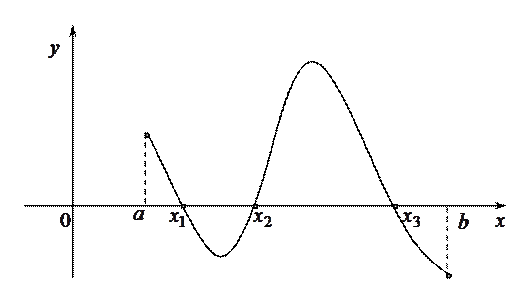
Замечание. Если непрерывна и монотонна на 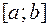,то существует не более одной точки , такой, что .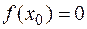

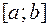Теорема (о промежуточных значениях). Пусть непре­рывна на отрезке и 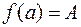, 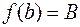. Тогда для любого числа 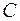, заключенного между 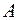и 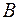, найдется такая точка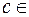 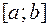, что .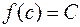

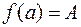Эта теорема геометрически очевидна. Рассмотрим график функ­ции . Пусть и .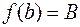

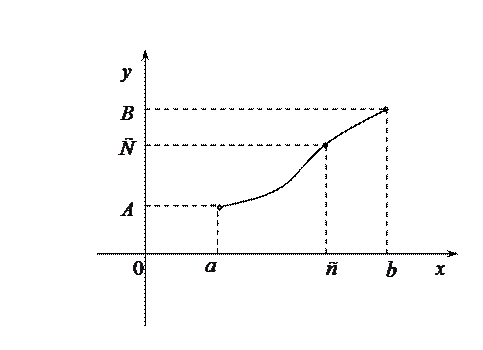
Тогда прямая 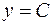, где 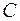— любое число, заключенное между 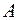и 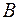, пересечет график функции по крайней мере в одной точке. Если же непрерывна и монотонна на 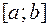, то существует единственная точка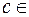 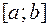, такая, что .

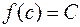Теорему о промежуточных значениях можно переформулировать так: непрерывная функ­ция, переходя от одного значения к другому, обязательно прини­мает все промежуточные значения.

В курсе математического анализа встречаются кусочно-непрерывные на отрезке 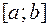функции.

Определение. Функция называется кусочно-непрерывной на от­резке 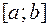, если она непрерывна во всех внутренних точках 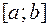за исклю­чением, быть может, конечного числа точек, в которых эта функция имеет разрыв первого рода или устранимый разрыв, и, кроме того, она имеет односторонние пределы в точках 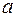и .

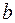Функция называется кусочно-непрерывной на числовой пря­мой, если она кусочно-непрерывна на любом отрезке этой прямой.