Элементарные операции

Операции, с помощью которых из простейших базовых функций могут быть получены различные рекурсивные функции, называют элементарными.

Операция суперпозиции. Если даны:

· рекурсивная функция h^(m)=(z₁, z₂,…, z_m,, у| z_i, y∈N),

· m рекурсивных функций g_i⁽ⁿ⁾=(x_1i, x_2i,..., x_ni, z_i| x_ji, z_i∈N),

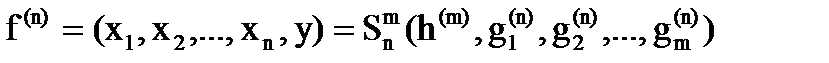то в результате подстановки 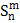функций g₁⁽ⁿ⁾, g₂⁽ⁿ⁾,…, g_m⁽ⁿ⁾ вместо независимых переменных функции h^(m) может быть получена новая функция f⁽ⁿ⁾=(x₁, x₂,..,, x_n, у) от n независимых переменных:

Значения z_i функций g₁⁽ⁿ⁾, g₂⁽ⁿ⁾,..., g_m⁽ⁿ⁾, найденные для известных значений независимых переменных из множества {x_j} (jÎ{1,2,…,n}) принимаются за значения независимых переменных из множества {z_i}, iÎ{1,2,…,m}, аргумента функции h^(m). Затем вычисляется ее значение y, которое принимается за значение функции f⁽ⁿ⁾=(x₁, x₂,..., x_n, y). Таким образом, суперпозиция выполняется по схеме:

gj(n)

h(m)

x₁=a₁ x₂=a₂... x_n=a_n

z₁ z₂... z_m

y

Основные свойства функций, вычисляемых с помощью оператора суперпозиции:

· если вычислимы функции h^(m) и g_i⁽ⁿ⁾, то вычислима также функция, соответствующая оператору суперпозиции;

· если даны функции тождества I_n^m и оператор суперпозиции S_n^m, то заданными являются любые операторы подстановки, перестановки и переименования любых независимых переменных аргумента;

· если среди функций g_i⁽ⁿ⁾ имеется хотя бы одна частично рекурсивная, то и функция f⁽ⁿ⁾ также будет частичной.

Операция рекурсии. Если даны:

· рекурсивная функция g⁽ⁿ⁾(x₁,x₂,…,x_n| x_i∈N),

· рекурсивная функция h⁽ⁿ⁺²⁾(x₁,x₂,…,x_n,y,f⁽ⁿ⁺¹⁾(x₁,x₂,…,x_n,y) | x_i, y∈N),

то, применяя оператор рекурсии R, можно найти рекурсивную функцию 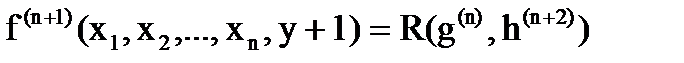, используя схему примитивной рекурсии:

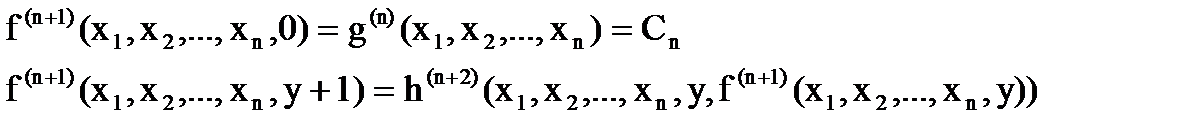
Дополнительный аргумент y функции h⁽ⁿ⁺²⁾ указывает, при каком его значении следует определять значение функции f⁽ⁿ⁺¹⁾(x₁, x₂,…, x_n, y) для вычисления последующих значений функции f⁽ⁿ⁺¹⁾(x₁,x₂,…, x_n, y+1).

При исполнении операции рекурсии известными являются x₁=a₁, x₂=a₂,..., x_n=a_n. Принимают y=0 и вычисляют функцию g⁽ⁿ⁾. Ее значение, равное Сⁿ, есть значение функции f⁽ⁿ⁺¹⁾. Это значение подставляется в функцию h⁽ⁿ⁺²⁾ в качестве аргумента f⁽ⁿ⁺¹⁾(x₁, x₂,…, x_n, y). Значением функции f⁽ⁿ⁺¹⁾ для каждого последующего значения аргумента y - (у+1) - следует считать значение функции h⁽ⁿ⁺²⁾, вычисленное по значению аргумента у и по значению аргумента f⁽ⁿ⁺¹⁾(x₁, x₂,..., x_n, у). Таким образом, рекурсия выполняется по схеме:

g(n)

h(n+2)

x₁=a₁ x₂=a₂... x_n=a_n

C_n= f⁽ⁿ⁺¹⁾ при y=0

f⁽ⁿ⁺¹⁾

При задании примитивно рекурсивного описания функции f, не имеющей независимых переменных x, но зависящей от одной дополнительной переменной y, схема примитивной рекурсии имеет вид:

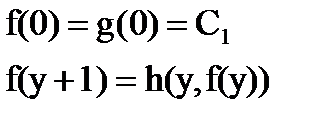
Операция минимизации ( или поиск наименьшего корня). Если дана рекурсивная функция f(x₁, x₂,..., x_n, у), то рекурсивную функцию ϕ(x₁, x₂,..., x_n) можно вычислить при заданных x₁=a₁, x₂=a₂,..., x_n=a_n, придавая вспомогательному аргументу у последовательно значения 0, 1, 2,..., пока f(a₁, a₂,..., a_n, у) ни окажется в первый раз (!) равной нулю, т.е. f(a₁, a₂,..., a_n, у)=0. Полученное значение у принять за значение определяемой функции, т.е. y = ϕ(a₁, a₂,..., a_n). Поиск значений функции ϕ(x₁, x₂,..., x_n) выполняется с помощью μ - оператора: j(x₁,x₂,...,x_n) = μ_y(f(x₁,x₂,...,x_n,y) = 0).

Алгоритм вычисления функции ϕ(a₁, a₂,..., a_n):

шаг 1: принять у=0 и вычислить функцию f(a₁,a₂,...,a_n,у),

шаг 2: если f(a₁,a₂,...,a_n,у)=0, то ϕ(a₁,a₂,...,a_n)=у, конец; иначе у=у+1, шаг 1.

Операция итерации. Многократное повторение данного процесса, пока ни будет выполнено некоторое условие, называют итерацией. При этом на каждом шаге итерации данный процесс выполняется полностью. Условием итерации, как правило, является число повторений: f(n)=Jⁿ(h), где h – функция, формирующая новую функцию f(i+1) итеративной процедурой для 1 ≤ i ≤ n, начальное значение которой f(0)=0: f(0)=0, f(i+1) = h(f(i)).

Функция называется примитивно рекурсивной, если она получена из базовых функций с помощью конечного числа операторов суперпозиции и/или примитивной рекурсии. Она же называется рекурсивной, если получена с помощью примитивно рекурсивных функций и конечного числа операторов суперпозиции, примитивной рекурсии и/или минимизации. Иначе говорят так: функции, для которых существуют алгоритмы вычисления, называют рекурсивными функциями. Рекурсивная функция называется частично рекурсивной, если она определена не на всем множестве целых положительных чисел и общерекурсивной, если она определена на всем множестве целых положительных чисел.