Выбор частоты дискретизации

И так, если мы хотим, чтобы обработка аналоговых сигналов осуществлялась с помощью вычислительной (микропроцессорной) техники, непрерывные сигналы должны быть с помощью АЦП представлены в виде последовательности отдельных цифровых отсчетов. Производительность вычислительных средств при этом должна быть такой, чтобы после получения очередного отсчета до получения следующего отсчета программно были выполнены все необходимые действия по обработке отсчета. При выполнении любой задачи мы хотим обойтись простейшими (и, следовательно, максимально дешевыми) средствами. В случае применения вычислительной техники это означает использование техники с низкой производительностью. Желание использования техники с низкой производительностью будет означать в свою очередь то, что мы будем стараться по возможности брать отсчеты входного сигнала (проводить его дискретизацию по времени) по возможности с меньшей частотой.

Возникает вопрос: с какой наименьшей частотой мы можем производить дискретизацию (брать отсчеты, выборки) входного сигнала? Очевидно, что если мы будем брать отсчеты слишком редко, то в них не будет содержаться информация о быстро меняющемся сигнале. Скорость изменения сигнала характеризуется шириной (верхней частотой) его спектра. Таким образом, интуитивно понятно, что минимально допустимая частота дискретизации связана с наибольшей частотой спектра сигнала. Как же более конкретно связать эти понятия между собой?

Поставленные вопросы можно сформулировать по-другому, рассудив следующим образом. Хотя цифровой сигнал определяет непрерывный сигнал только по отдельным отсчетам, мы не должны терять информацию о поведении сигнала – вычислительная система, получающая цифровой сигнал, должна воспринимать его адекватно исходному непрерывному. Очевидна справедливость утверждения о том, что информацию о поведении сигнала после представления его отдельными отсчетами мы не потеряли, если по этим отдельным отсчетам можно опять восстановить форму исходного сигнала. Тогда решаемый вопрос, можно сформулировать так: с какой минимальной частотой можно брать отсчеты, чтобы иметь возможность по ним восстановить исходный сигнал?

Возможность восстановления сигнала по его дискретным отсчетам, связь частоты взятия этих отсчетов с частотными свойствами сигнала определяет теорема Котельникова. Теорема, которая имеет фундаментальное значение в физике и технике была доказана В. А. Котельниковым в 1933 г. и впервые опубликована им в работе «О пропускной способности «эфира» и проволоки в электросвязи». В соответствии с этой теоремой аналоговый сигнал x(t) при определённых условиях однозначно представляется последовательностью своих отсчётов, взятых через равные промежутки времени. В зарубежной литературе эта теорема называется теоремой отсчётов, в отечественной – теоремой Котельникова.

Для случая равномерной дискретизации она гласит: если непрерывный сигнал x(t) имеет спектр, ограниченный частотой F_B, то сигнал может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятыми с частотой F_Д = 2F_B.

Для того чтобы понять условия дискретизации и восстановления сигнала, выражаемые теоремой Котельникова, необходимо представлять как изменяется спектр сигнала после дискретизации сигнала.

Рассмотрим сначала очевидный случай. Представим себе синусоидальный сигнал в непрерывной форме и после дискретизации. Как известно спектр показывает, из каких гармонических составляющих может быть составлен сигнал. Синусоидальный сигнал состоит из одной гармоники. Если этот сигнал продискретизировать очевидно, что его спектр будет складываться из гармонической составляющей, соответствующей не дискретизированному сигналу, и высокочастотных гармоник, появившихся из-за наличия в форме дискретизированного сигнала ступенек. Данные рассуждения можно распространить и для анализа более сложных по форме (спектру) сигналов. Можно проводить и математический анализ, который в конечном итоге показал бы следующее.

Спектр дискретизированного сигнала будет состоять из спектра исходного сигнала, а также из высокочастотных составляющих, которые по форме будут повторять форму спектра исходного сигнала и их зеркальные отражения. Эти высокочастотные составляющие (частичные спектры) будут периодически повторяться на частотной оси с периодом кратным частоте дискретизации F_Д (центры частичных спектров будут лежать на частотах nF_Д, n = 1… ∞).

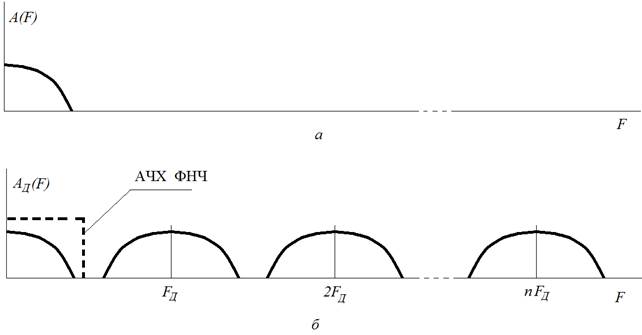
Рис.. Спектр непрерывного сигнала до (а) и после (б) дискретизации

При этом любой из частичных спектров является неискажённой копией исходного спектра, поэтому, в принципе, по любому из них можно восстановить исходный спектр, т. е. точно восстановить сигнал. Проще всего это сделать для частичного спектра при n = 0, выделив его с помощью фильтра низких частот (ФНЧ). На рис. показана идеальная амплитудно-частотная характеристика (АЧХ) такого фильтра.

Сформулируем ответ, следующий из этой теоремы, на поставленный нами выше вопрос. Т. к. можно по отдельным отсчетам восстановить исходный сигнал, то цифровой сигнал при правильном выборе частоты дискретизации полностью сохраняет (несет) информацию, которую содержит исходный не дискретизированный сигнал. И, следовательно, работать с цифровым сигналом можно так же как если бы мы работали с непрерывным сигналом – заниматься обработкой несущей цифровым сигналом информации, формировать на основании его управляющие воздействия и т. п.