Теорема. Всякий вектор  может быть представлен в виде линейной комбинации всех координатных ортов с проекциями рассматриваемого вектора на соответствующие координатные оси, т.е.
может быть представлен в виде линейной комбинации всех координатных ортов с проекциями рассматриваемого вектора на соответствующие координатные оси, т.е.
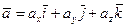 .
.
Здесь используются обозначения: 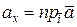 ,
, 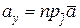 ,
, 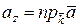 .
.
Доказательство.
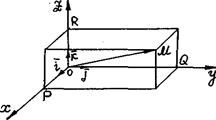 Совместим начало вектора
Совместим начало вектора  с началом декартовой системы координат, т.е. построим вектор
с началом декартовой системы координат, т.е. построим вектор 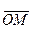 такой, что
такой, что 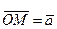 .
.
Построим составляющие вектора 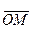 по координатным осям:
по координатным осям:
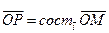 ,
, 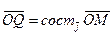 ,
, 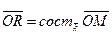 .
.
Согласно определению суммы векторов,
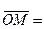
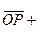
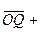
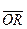 , или, что то же самое,
, или, что то же самое, 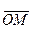
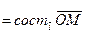
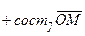
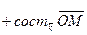 .
.
Если применить теперь теорему о связи между составляющей вектора по оси и ортом этой оси, то получим 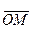
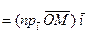
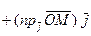
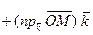 т.е.
т.е. 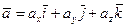 что и требовалось доказать.
что и требовалось доказать.
Теорема. Разложение вектора по координатным ортам единственно.
Доказательство. Пусть 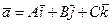 . Покажем, что
. Покажем, что 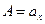 ,
, 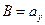 ,
, 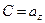 Вычислим проекцию вектора
Вычислим проекцию вектора 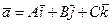 на ось
на ось 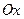 . На основании теоремы о проекции суммы векторов на ось
. На основании теоремы о проекции суммы векторов на ось 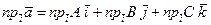 .
.
Воспользуемся теоремой о проекции на ось произведения вектора на скаляр. Тогда получим 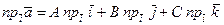 . Так как
. Так как 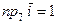 ,
, 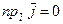 ,
, 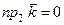 , то имеем
, то имеем 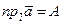 и потому
и потому 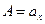 .
.
Аналогично можно доказать, что 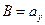 и
и 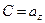
 2015-06-28
2015-06-28 4709
4709
