Разложение вектора ММ по координатным ортам

Теорема. Всякий вектор может быть представлен в виде линейной комбинации координатных ортов с разностями соответствующих одноименных координат конца и начала рассматриваемого вектора, т.е.

.

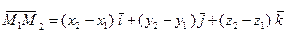где 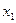, , 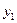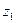- декартовы координаты точки 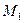, , 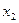, 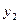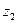- декартовы координаты точки .

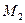Доказательство. Согласно теореме о разложении вектора по коорди­натным ортам, имеем

,

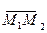
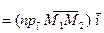
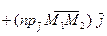
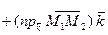или, с учетом теоремы о проекции вектора на числовую ось,

.

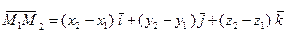Утверждение доказано.

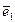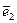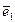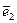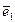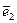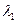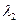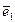Определение. Совокупность двух векторов и называется базисом плоскости, если любой вектор, расположенный в плоскости векторов и , может быть представлен в виде линейной комбинации векторов и с некоторыми числами и , т.е. для любого вектора , расположенного в плоскости векторов и 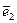, существуют числа 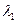и 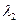такие, что 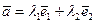. Можно доказать, что совокупность любых двух неколлинеарных векторов является базисом плоскости. Аналогично вводится понятие базиса пространства.

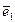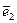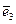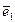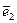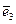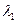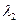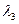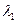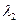Определение. Совокупность трех векторов , и называется базисом пространства, если любой вектор в пространстве может быть представлен в виде линейной комбинации векторов , и , с некоторыми числами , и , т.е. для любого вектора в пространстве существуют числа , и 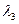, такие, что .

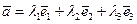В теореме о разложении вектора по координатным ортам было показано, что для любого вектора справедливо равенство

.

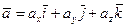Следовательно, совокупность ортов 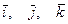является базисом пространства.

Можно доказать, что совокупность любых трех некомпланарных векторов является базисом пространства.