Находить СКНФ для функции также можно по ее таблице истинности, но дизъюнкции берутся по тем наборам, где функция =0. С отрицанием берется та переменная, значение которой =1.
Например таблицей задана функция от трех переменных равная 1, если большинство аргументов равно 1.
Таб. 5
| Х | Y | Z | f |
Данная функция имеет следующую СКНФ:
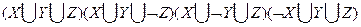 .
.
Однако, если функция задана формулой, то строить СКНФ по таблице не рационально, тогда применяют следующий алгоритм: построение СКНФ состоит из двух этапов, каждых из которых состоит их трех шагов. На первом этапе строят КНФ, а на втором этапе из КНФ строят СКНФ.
1 шаг. Преобразуем формулу так, чтобы в ней были операции только дизъюнкции, конъюнкции, и отрицания (причем отрицание должно быть простым, т. е. над каждым аргументом). При помощи следующих действий можно устранить импликацию, эквивалентность и произвести перенос отрицания:
|
|
|
· импликация 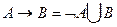
· эквивалентность 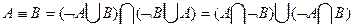
· перенос отрицания: из свойств: 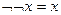 и
и 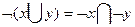 можно произвести следующие преобразования:
можно произвести следующие преобразования: 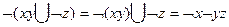
2 шаг. Преобразуем функцию так, чтобы все дизъюнкции выполнялись раньше, чем конъюнкции. Достичь этого можно при помощи свойства дистрибутивности дизъюнкции относительно конъюнкции:
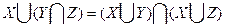
 .
.
Например: 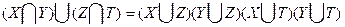
3 шаг. Если в КНФ имеется несколько одинаковых элементарных дизъюнкций, то мы оставляем только одну (используя свойство идемпотентности: 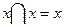 ).
).
4 шаг. Делаем все элементарные конъюнкции правильными путем одним из следующих преобразований:
· если в элементарную дизъюнкцию входит некоторая переменная вместе со своим отрицанием, то мы удаляем эту дизъюнкцию из КНФ (используя свойство 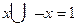 ).
).
· Если некоторая переменная входит в элементарную конъюнкцию несколько раз, причем или во всех функциях с отрицанием или во всех случаях без отрицания, то мы оставляем только одно вхождение (используя свойство идемпотентности: х 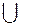 х = х).
х = х).
5 шаг. Делаем все элементарные дизъюнкции полными. Если в некоторую дизъюнкцию 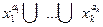 не входит переменная y, то необходимо рассмотреть равносильное выражение
не входит переменная y, то необходимо рассмотреть равносильное выражение 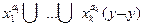 и вновь применить шаг 2. Если недостающих переменных несколько, то нужно добавить несколько дизъюнктивных членов вида
и вновь применить шаг 2. Если недостающих переменных несколько, то нужно добавить несколько дизъюнктивных членов вида 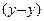 .
.
6 шаг. После применения 5-го шага могут вновь появится одинаковые дизъюнкции. Поэтому на шестом шаге применяют шаг 3.
Задание №5
Найти СКНФ для формулы:
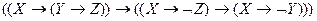 =
=
1. шаг. Преобразуем формулу так, чтобы в ней были операции только конъюнкции, дизъюнкции и отрицания.
Используя свойство 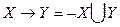 , получим
, получим
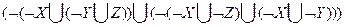 =
=
используя свойство 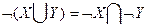 ,получим
,получим 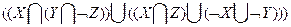 =
=
|
|
|
2. шаг. Преобразуем формулу так, чтобы дизъюнкция выполнялась раньше, чем конъюнкция.
Используя свойство дистрибутивности получим
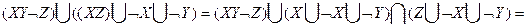
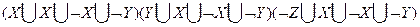
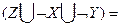
3. шаг. Делаем дизъюнкции правильными
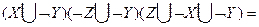
4. шаг. Делаем дизъюнкции полными
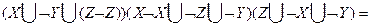
5. шаг. Применяем шаг 2. Получаем
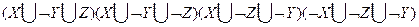
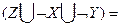
6. шаг. Получили две одинаковые дизъюнкции, оставляем одну из них
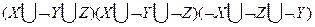
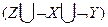
получили совершенную конъюнктивную нормальную форму. (в конце примера опущен знак конъюнкции)
 2015-06-28
2015-06-28 1082
1082








