29.
Комівояжеру необхідно відвідати кожне місто в межах конкретної зони обслуговування і повернутися додому. Комівояжеру хотілося б вибрати такий порядок обходу клієнтів, при якому його шлях був можливо коротше. Таким чином, комівояжер стикається із завданням пошуку маршруту мінімальної протяжності, тривалості або вартості.
Задача комівояжера може бути сформульована як задача на графі в такій постановці: побудувати граф G (V, E), вершини якого відповідають містам у зоні комівояжера, а дуги відображають комунікації, що з'єднують пари міст. Нехай довжина e (х, у)≥0 кожної дуги 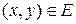 дорівнює відстані, вартості або часу. Контур, що включає кожну вершину графа G хоча б один раз, називається маршрутом комівояжера. Контур, що включає кожну вершину графа G рівно один раз, називається гамільтоновим контуром (по імені ірландського математика Вільяма Роуана Гамільтона, який в 1859 р. першим почав вивчення цих задач).
дорівнює відстані, вартості або часу. Контур, що включає кожну вершину графа G хоча б один раз, називається маршрутом комівояжера. Контур, що включає кожну вершину графа G рівно один раз, називається гамільтоновим контуром (по імені ірландського математика Вільяма Роуана Гамільтона, який в 1859 р. першим почав вивчення цих задач).
Загальною задачею комівояжера називається задача пошуку маршруту найменшої загальної довжини.
Задачею комівояжера називається задача пошуку гамільтонового контуру найменшою загальної довжини. Контур комівояжера, що має найменшу довжину, називається оптимальним маршрутом комівояжера і є оптимальним рішенням загальної задачі комівояжера. Гамільтонов контур найменшої довжини називається оптимальним гамільтоновим контуром і є оптимальним рішенням задачі комівояжера.
Алгоритм Літтла використовують для пошуку рішення задачі комівояжера у виді гамільтонова контуру. Даний алгоритм використовується для пошуку оптимального гамільтонова контуру в графі, що має N вершин, причому кожна вершина i зв’язана з будь-якою іншою вершиною j двонаправленою дугою. Кожній дузі приписана вага Сi,j, причому вага дуг строго позитивна (Сi,j ≥ 0). Вага дуг утворюють матрицю вартості. Всі елементи по діагоналі матриці прирівнюють до нескінченності (Сi,j = ∞).
У випадку, якщо пара вершин i та j не зв'язана між собою (граф неповнозв'язний), то відповідному елементу матриці вартості приписуємо вагу, що дорівнює довжині мінімальному шляху між вершинами i и j. Якщо в результаті дуга (i, j) увійде в результуючий контур, то її необхідно замінити відповідним їй шляхом. Матрицю оптимальних шляхів між усіма вершинами графа можна отримати застосувавши алгоритм Данцига або Флойда.
Алгоритм Літтла є окремим випадком застосування методу "гілок і меж" для конкретного завдання. Загальна ідея тривіальна: потрібно розділити величезне число варіантів, що перебираються, на класи і отримати оцінки для цих класів, щоб мати можливість відкидати варіанти не по одному, а цілими класами. Складність полягає в тому, щоб знайти такий поділ на класи (гілки) і такі оцінки (межі), щоб процедура була ефективною.
Алгоритм Літтла
1. У кожному рядку матриці вартості знайдемо мінімальний елемент і віднімемо його з усіх елементів рядка. Зробимо це і для стовпців, що не містять нуля. Отримаємо матрицю вартості, кожен рядок і кожен стовпець якої містять хоча б один нульовий елемент.
2. Для кожного нульового елемента матриці cij розрахуємо коефіцієнт Гi,j, що дорівнює сумі найменшого елемента i строки (виключаючи елемент Сi,j = 0) і найменшого елемента j стовпця. З усіх коефіцієнтів Гi,j виберемо такий, який є максимальним Гk,l = max{ Гi,j }. У гамільтонів контур вноситься відповідна дуга (k,l).
3. Вилучаємо k -ту строку та стовпець l, поміняємо на нескінченність значення елемента Сl,k (оскільки дуга (k,l) включена в контур, то зворотний шлях з l в k неприпустимий).
4. Повторюємо алгоритм з кроку 1, поки порядок матриці не дорівнюватиме двом.
5. Потім у поточний орієнтований граф вносимо дві відсутні дуги, що визначаються однозначно матрицею порядку 2. Отримуємо гамільтонів контур.
У ході вирішення ведеться постійний підрахунок поточного значення нижньої межі. Нижня межа дорівнює сумі всіх забраних елементів у рядках і стовпцях. Підсумкове значення нижньої межі повинне збігтися з довжиною результуючого контуру.
30. Розфарбування вершин графа G (V, Е) l фарбами називається розбиття множини вершин V графа G, при якому кожна підмножина V i не містить жодної пари суміжних вершин
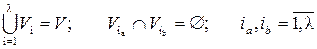 .
.
Іншими словами, розфарбування графа l фарбами називається правильною, якщо у кожного його ребра початок розфарбований в один колір, а кінець – в інший колір, тобто суміжні вершини графа розфарбовані різними кольорами.
Стосовно до розфарбування графів зазвичай виділяють три види задач:
1) Визначення хроматичного числа графа, тобто найменшої кількості кольорів, якими можна правильно розфарбувати граф. Практичного способу точного визначення хроматичного числа графа не існує. У загальному випадку мається гіпотеза про чотири фарби (яка не доведена і не спростована), яка стверджує, що для плоского графа l(G) £ 4.
Окремим випадком цієї задачі є перевірка графа на біхроматичність, яка виконується на основі теореми Кеніга.
Хроматичне число графа може бути оцінено через його параметри (степінь вершин і вершинне число незалежності):
а) якщо максимальна степінь вершини графа дорівнює dmax(G), то хроматичне число графа не перевищує величини dmax(G) + 1, тобто l(G) £ dmax(G) + 1;
б) для будь-якого графа G (V, Е) з вершинним числом незалежності b0(G) справедливе твердження:
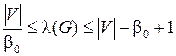 .
.
2) Виконання правильного розфарбування графа. Ця задача при відомому хроматичному числі є досить простою і вирішується евристично. Одна з вершин використовується в якості початкової і розфарбовується довільним кольором, всі суміжні з нею вершини розфарбовуються іншими кольорами з урахуванням їх суміжності між собою і т.д.
3) Визначення числа правильних розфарбувань графа з відомим хроматичним числом. Для невеликих графів число правильних розфарбувань з використанням l фарб визначається за формулою:
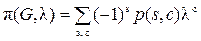 ,
,
де s – число ребер в підграфі;
с – кількість компонент зв'язності в підграфі;
р (s, с) – число підграфів з s ребрами і с компонентами зв'язності.
Для графа G, що має n вершин та m ребер, параметр s буде приймати значення від 0 до m, а параметр с – від n до 1 (звичайно, що s та с – цілі числа). Для того, щоб уникнути помилок при підрахунку числа підграфів р (s, с) можна скористатися формулою
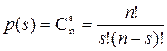 ,
,
враховуючи при цьому такі обставини:
· 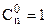 для будь-якого n (оскільки 0! = 1);
для будь-якого n (оскільки 0! = 1);
· значення р (s) розраховується для кожного значення s, без урахування значення с.
· Лема 1: Якщо графи G 1 та G 2 не пов'язані, тобто являють собою компоненти зв'язності графа G (рис. 5.2), то
·
· 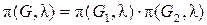 .
.
· 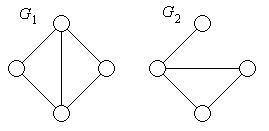
· Рис. 5.2
·
· Лема 2: Якщо граф G має точку зчленування v С (рис. 5.3), то
·
· 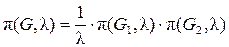 .
.
·
· 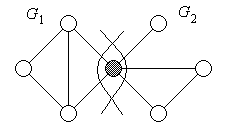
· Рис. 5.3
·
· Лема 3: Якщо граф G має міст е С (рис. 5.4), то
·
· 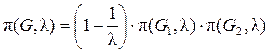 .
.
·
· 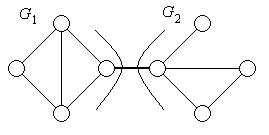
· Рис. 5.4
·
· Лема 4: Якщо граф G отриманий з графа G 1 додаванням ребра е без зміни числа вершин (рис. 5.5), то
·
· 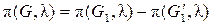
 2015-06-28
2015-06-28 843
843






