2015-01-30
168400
№ 1. Зависимость выпуска продукции от количества используемого труда отображается функцией:
.
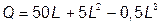1. При каком количестве используемого труда достигается максимум:
а) общего выпуска;
б) предельной производительности (предельного продукта) труда;
в) средней производительности (среднего продукта) труда.
2. Определите эластичность выпуска по труду при использовании 5 ед. труда.
Решение
1а. Функция от одной переменной достигает максимума, когда ее производная равна нулю. С учетом того, что L > 0, получаем:
.
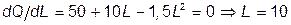1б. Предельная производительность труда
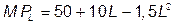
достигает максимума при 10 = 3 L Þ L = 10/3.
1в. Средняя производительность труда
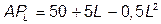
достигает максимума при L = 5.
2. По определению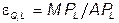 
. При L = 5 средняя и предельная производительности равны 62,5; следовательно, 
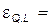1.
№ 2. Фирма работает по технологии, отображаемой производственной функцией Q = L 0,75 K 0,25. Факторы производства она покупает по неизменным ценам: w = 144; r = 3.
Определите в состоянии равновесия фирмы:
а) среднюю производительность труда (продукт труда);
б) среднюю производительность капитала (продукт капитала);
в) предельную производительность труда;
г) предельную производительность капитала.
Решение
а)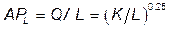 
. Условие равновесия фирмы MRTSL,K = w/r.
.
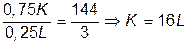Следовательно: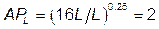 
.
б)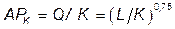 
→ 
;
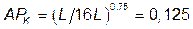в)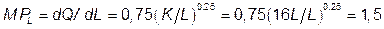 
;
г)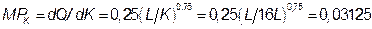 
.
№ 3. Технология производства фирмы задана производственной функцией: Q = 20 L 0,5. Цена труда w = 2, а цена продукции фирмы Р = 5.
Определите:
а) выпуск фирмы;
б) общие затраты на выпуск;
в) средние затраты;
г) предельные затраты;
д) объем спроса фирмы на труд.
Решение
а) В соответствии с технологией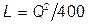 
. Поэтому 
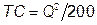и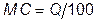 
.
По условию максимизации прибыли
;
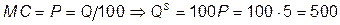б) TC = 5002/200 = 1250; в) AC = 1250/500 = 2,5;
г) MC = 500/100 = 5; д) L = 5002/400 = 625.
№ 4. Фирма, максимизирующая прибыль, работает по технологии Q = L 0,25 K 0,25. Факторы производства она покупает по неизменным ценам: w = 2; r = 8 и продает свою продукцию по цене Р = 320.
Определите:
а) выпуск фирмы;
б) общие затраты на выпуск;
в) средние затраты;
г) предельные затраты;
д) объем спроса фирмы на труд;
е) объем спроса фирмы на капитал;
ж) прибыль фирмы;
з) излишки продавца.
Решение
 |
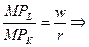а) Условие равновесия фирмы:
.
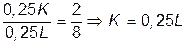В соответствии с технологией: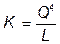 
. Следовательно,
.
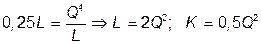Тогда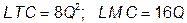 
. Из условия максимизации прибыли следует 
;
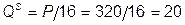б) LTC = 8×202 = 3200; в) LAC = 3200/20 = 160;
г) LMC = 16×20 = 320; д) L = 2×400 = 800;
е) K = 0,5×400 = 200; ж) 20×320 – 3200 = 3200;
з) 0,5•20•320 = 3200.
№ 5. Предприятие работает по технологии, описываемой производственной функцией: Q = LαKβ, бюджетное ограничение имеет вид: C(Q) = wL + rK. Найти оптимум производителя (минимизация затрат в длительном периоде) методом Лагранжа.
Решение:
1. Функция Лагранжа имеет вид:
Ф = wL + rK + μ(Q - LαKβ), где μ – множитель Лагранжа, переменная.
2. Продифференцировать функция Лагранжа по L, K, μ:
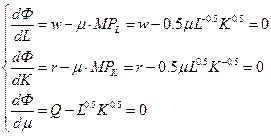
Последнее уравнение представляет собой производственное ограничение.
3. Решить уравнения для L, K и μ. В результате получаем:
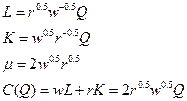
№ 6. Фирма с функцией общих затрат
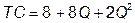
может продать любое количество своей продукции по цене Р = 20.
1. Определите выпуск фирмы:
а) минимизирующий средние затраты;
б) максимизирующий прибыль.
2. Рассчитайте максимальную величину:
а) прибыли;
б) излишка производителя.
3. Определите эластичность предложения фирмы по цене, когда она получает максимум прибыли.
Решение
1а.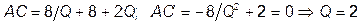 
.
1б.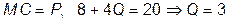 
.
2а. p = 20×3 – 8 – 8×3 – 2×9 = 10.
2б. D = 20×3 – 8×3 – 2×9 = 18.
3. 
.
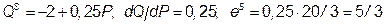№ 7. При цене 8 ден. ед. за 1 кг фермер, имеющий линейную функцию предложения, продал 10 кг яблок. Эластичность предложения по цене равна 1,6. Сколько кг яблок продаст фермер, если цена будет равна 12 ден. ед?
Решение
Общий вид линейной функции предложения: QS = m + nP. Для нее eS = nP*/Q* Þ n = eSQ*/P*; m = Q*(1 – eS).
В условиях задачи n = 2; m = 6; следовательно, функция предложения имеет вид:
QS = –6 + 2P; при цене 12 объем предложения равен 18.
№ 8. Н а рынке имеются три продавца со следующими функциями предложения:
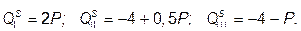
Определите эластичность рыночного предложения по цене, когда на рынке продается 11 ед. товара.
Решение
Для определения интервалов цен, соответствующих различным наклонам кривой рыночного предложения, перейдем от индивидуальных функций предложения к индивидуальным функциям цены предложения:
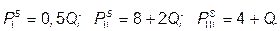
Следовательно, в интервале 0 < P £ 4 рыночное предложение представлено продавцом I; в интервале 4 < P £ 8 рыночное предложение равно сумме предложения I и III продавцов, и только после P > 8 рыночное предложение равно сумме всех трех продавцов:
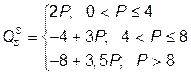
Отсюда видно, что 11 ед. товара будет продано по цене Р = 5; тогда eS = 3×5/11 = 15/11.
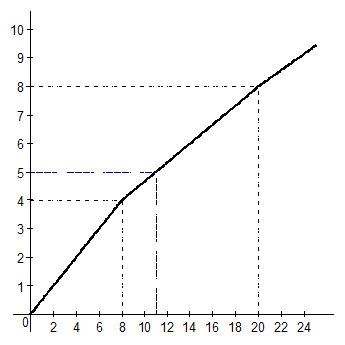
Рис. 2.1. Рыночное предложение как сумма индивидуальных предложений
1. Какую конфигурацию могут иметь изокванты? Приведите примеры взаимозаменяемых и взаимодополняемых ресурсов в практических ситуациях. Какое значение при этом может иметь показатель предельной нормы технической замены?
2. Как согласуются между собой показатели общего выпуска, предельной производительности и средней производительности фактора производства? В каких случаях фирма (отрасль) может преследовать цели максимизации каждого из перечисленных показателей?
3. Проанализируйте разницу между убывающей отдачей от масштаба и убывающей предельной производительностью фактора. Приведите примеры рассматриваемых процессов. Может ли специализация (разделение труда) привести к положительному эффекту масштаба?
4. Что представляет собой эластичность выпуска от переменных факторов производства? Как данные показатели согласуются с эластичностью выпуска от масштаба для производственной функции Кобба-Дугласа?
5. Может ли функция предельной производительности труда демонстрировать возрастающий характер? Приведите практические примеры.
6. Как трактуется понятие технический прогресс в теории микроэкономики? Какими допущениями теории это обусловлено? В чем основные недостатки такой трактовки?
7. Проанализируйте понятия «затраты», «издержки», «стоимость». Каковы, на Ваш взгляд, различия между данными понятиями и можем ли мы с точки зрения микроэкономики использовать какие-то из них в качестве синонимов?
8. Какие затраты могут быть отнесены к постоянным для целлюлозно-бумажного комбината, фермы по разведению карпов, фирмы, осуществляющей грузовые перевозки, газетного киоска, интернет-магазина. Какой временной промежуток может составлять короткий период для перечисленных фирм?
9. Почему функции затрат короткого периода всегда располагаются выше функции затрат длительного периода? Всегда ли огибающая снизу функция LATC касается соответствующей функции SATC в точке минимума последней?
10. Как согласуется эластичность предложения по цене с различными параметрами рыночной конъюнктуры и особенностями товара? Обоснованно предположите уровень коэффициента эластичности предложения для следующих категорий товаров: мороженое, елочные игрушки, старинные монеты, меховые шапки из норки, лак для волос Taft, малолитражные автомобили, ядерные ракетоносцы?
Задачи
№1№. Заполните пропуски в следующей таблице:
| Объем применения переменного ресурса, L | Общий выпуск продукции, Q | Предельный продукт переменного ресурса, МРL | Средний продукт переменного ресурса, АРL |
| … | ... | ||
| … | … | ||
| … | … | ||
| … | … | ||
| … | … |
1. изобразите линии общего выпуска, предельного и среднего продуктов труда;
2. объясните, почему полученные линии имеют такие конфигурации;
3. всегда ли равенство среднего и предельного продуктов переменного фактора указывает на максимальное значение среднего продукта? Почему?
4. выделите на графике три стадии производства;
5. всегда ли предельный продукт положителен? Почему?
6. найдите значение эластичности выпуска по труду при L = 5.
№2. Заполните пропуски в следующей таблице:
| Объем применения переменного ресурса, L | Общий выпуск продукции, Q | Предельный продукт переменного ресурса, МРL | Средний продукт переменного ресурса, АРL |
| ... | |||
| … | … | ||
| … | ... | ||
| … | … | ||
| … | ... |
№3.
| Объем применения переменного ресурса, L | Общий выпуск продукции, Q | Предельный продукт переменного ресурса, МРL | Средний продукт переменного ресурса, АРL |
| ... | |||
| … | … | ||
| … | ... | ||
| … | … | ||
| … | ... |
Найти значение предельного продукта 7-й единицы фактора
№4
| Объем применения переменного ресурса, L | Общий выпуск продукции, Q | Предельный продукт переменного ресурса, МРL | Средний продукт переменного ресурса, АРL |
| … | … | ||
| … | … | ||
| … | … | ||
| … | … | ||
| … | ... |
Найти значение общего выпуска при L = 5.
№5. Зависимость выпуска продукции от количества используемого труда отображается функцией
.
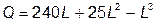1. При каком количестве используемого труда достигается максимум:
а) общего выпуска;
б) предельной производительности (предельного продукта) труда;
в) средней производительности (среднего продукта) труда.
2. Найдите максимальные значения общего выпуска, предельного и среднего продуктов труда;
3. Изобразите линии общего выпуска, предельного и среднего продуктов труда;
4. объясните, почему полученные линии имеют такие конфигурации;
5. всегда ли равенство среднего и предельного продуктов переменного фактора указывает на максимальное значение среднего продукта? Почему?
6. выделите на графике три стадии производства;
7. всегда ли предельный продукт положителен? Почему?
8. Определите эластичность выпуска по труду при использовании 5 ед. труда.
№6. Зависимость выпуска продукции от количества используемого труда отображается функцией: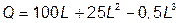 
. Определите максимум: а) общего выпуска; б) предельной производительности труда; в) средней производительности труда.
№7. Фирма работает по технологии, отображаемой производственной функцией Q = 10L0,75K0,25. Факторы производства она покупает по неизменным ценам: w = 24; r = 8.
Определите в состоянии равновесия фирмы:
а) среднюю производительность труда (продукт труда);
б) среднюю производительность капитала (продукт капитала);
в) предельную производительность труда;
г) предельную производительность капитала.
№8. Фирма работает по технологии, отображаемой производственной функцией Q = 10 L 0,75 K 0,25. Факторы производства она покупает по неизменным ценам: w = 5; r = 1. Определите в состоянии равновесия фирмы: а) среднюю производительность труда (продукт труда); б) среднюю производительность капитала (продукт капитала); в) предельную производительность труда; г) предельную производительность капитала.
№ 9. Процесс производства на некотором предприятии описывается производственной функцией:
Q = 2L2/3 × K1/3,
где Q – объем производства, L – объем используемых трудовых ресурсов; K – объем используемого оборудования.
1. Каков экономический смысл показателей степеней при переменных L и К?
2. Найдите алгебраическое выражение для изокванты при Q = 4. Нарисуйте эту изокванту.
3. Объясните взаимосвязь между конфигурацией изокванты и значениями показателей степеней; что произойдет с изоквантой, если показатели степеней станут равны?
4. Допустим, ставка арендной платы за оборудование (r) вдвое выше ставки оплаты труда (w). Предприятие использует две единицы оборудования и две единицы труда. Может ли предприятие, изменив комбинацию используемых ресурсов, уменьшить затраты, не уменьшая выпуск продукции? Ответ представьте графически и алгебраически.
5. Какое значение имеют цены факторов и показатели степеней в производственной функции при оптимизации предприятия-производителя.
№10. Процесс производства на некотором предприятии описывается производственной функцией:
Q = 3L1/3 × K2/3,
где L – объем используемых трудовых ресурсов; K – объем используемого оборудования.
1. Найдите алгебраическое выражение для изокванты при Q = 6. Нарисуйте эту изокванту.
2. Ставка арендной платы за оборудование вдвое выше ставки оплаты труда. Предприятие использует две единицы оборудования и две единицы труда.
3. Может ли предприятие, изменив комбинацию используемых ресурсов, уменьшить затраты, не сокращая выпуск?
4. Почему для предприятия так важно достижение оптимума в производстве?
5. Какие последствия грозят предприятию, если оно не достигает оптимума в производстве?
№11. Предприятие производит объем продукции Q, используя такие объемы ресурсов, при которых предельный продукт оборудования превышает предельный продукт труда в 2 раза. Ставка оплаты за аренду единицы оборудования превышает ставку оплаты труда в 3 раза.
Может ли предприятие уменьшить затраты, не сокращая объема выпуска? Если да, то в каком направлении следует изменить соотношение между объемами используемого оборудования и труда? Поясните ответ с помощью изокванты и изокосты.
№12. Используя изображенный ниже рисунок, ответьте на следующие вопросы:
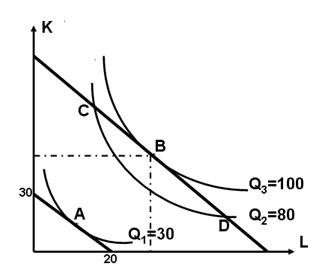
1. Какова предельная норма технической замены в точке A?
2. Если в точке B w = 4, r = 6 и фирма, находясь в этой точке, применяет 50 единиц капитала и 30 единиц труда, какова величина средних затрат для производства 100 единиц продукции?
3. Отражают ли точки C и D комбинацию факторов производства, которые используются для определения долгосрочных средних затрат при установлении цены на 80 единиц продукции? Объясните;
4. Что общего между точками С и D и чем они различаются?
5. О чем говорит конфигурация изоквант, представленных на рисунке?
6. Как изменилась бы конфигурация изоквант, если бы факторы характеризовались бы абсолютной заменяемостью? Дополняемостью? Приведите примеры подобных производств.
№13. Производственная функция фирмы имеет вид: Q =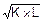 
. Пусть уровень выпуска равен 50 ед.
Какой будет оптимальная комбинация ресурсов K и L, если ставка зарплаты (w) равна 10 ден. ед., а ставка арендной платы за оборудование (r) равна 5 ден. ед.
№14. Фирма работает по технологии, отображаемой производственной функцией Q = L 1/4 K 1/4. Цена труда – 4 ден. ед., а цена капитала – 16 ден. ед. Сколько капитала будет использовать фирма при выпуске 20 ед. продукции?
№15. Фирма работает по технологии, отображаемой производственной функцией Q = L0,75 K0,25. Цена труда – 15ден. ед., а цена капитала – 5 ден. ед. Сколько труда будет использовать фирма при выпуске 75 ед. продукции?
№16. Фирма работает по технологии, отображаемой производственной функцией Q = L 0,6 K 0,4. Цена труда – 9 ден ед., а цена капитала – 3 ден ед.
Какова будет капиталовооруженность труда на этой фирме?
№17. Бюджет фирмы равен 200 ден. ед. Она работает по технологии, соответствующей производственной функции Q = L × K, при ценах на факторы: w = 2; r = 4.
а) При каких значениях L и K фирма достигает максимума выпуска?
б) Как изменится капиталовооруженность труда на фирме, если при той же цене труда цена капитала возрастет в 1,5 раза?
№18. Фирма может потратить на производство товара 900 ден. ед. Чтобы производить продукцию с минимальными средними затратами, фирма использует 120 ед. капитала по цене r = 5 и при этом предельная норма замещения капитала трудом равна – 1,5. Сколько единиц труда нанимает фирма?
№19. Бюджет фирмы равен 300 ден. ед. Она работает по технологии, соответствующей производственной функции Q = L0,6 K0,4, при ценах на факторы: w = 12; r = 18. При каких значениях K и L фирма достигает максимума выпуска?
№20. Предположим, фирма имеет следующие характеристики производственного процесса в коротком периоде: МРК=12, МРL= 20. Ставка заработной платы равна 8 ден. ед., а ставка арендной платы – 2 ден. ед. Как надо изменить количество применяемого труда и капитала, чтобы добиться оптимального их сочетания?
№21. Предельная норма технического замещения трудом капитала равна 4. На сколько необходимо сократить использование труда для того, чтобы обеспечить прежний объем производства при увеличении капитала на 8 единиц.
№22. Предположим производственная функция фирмы описывается уравнением Q = L1/2´K. На сколько процентов снизиться Q, если L снизиться на 19%, а К снизиться на 10%.
№23. Производство товара представляет собой такой процесс, при котором труд и капитал используются в соотношении 5 ч. труда на 1 ч. машинного времени. При удвоении факторов объем производства возрастает втрое (с 10 до 30 ед.). Когда факторы производства увеличиваются на половину (с 10 до 15 ч. труда и с 2 до 3 ч. машинного времени), выпуск удваивается (с 30 до 60 ед.) какой эффект масштаба демонстрирует производственная функция?
№24. Предположим, что когда фирма увеличивает применяемый капитал с 120 до 150 ед. и используемый труд с 500 до 625 ед., выпуск продукции увеличится с 200 до 220.
Какая отдача от масштаба производства (возрастающая, убывающая, постоянная) имеет место в данном случае?
№25. Допустим, фирма работает по технологии Q = L0,6 K0,4, при этом уменьшает объемы труда и капитала в два раза. Как изменится объем выпускаемой продукции?
№26. Если процесс производства на фирме характеризуется убывающей отдачей от масштаба при любом объеме производства, что произойдет с прибылью фирмы, если она разделится на два завода, каждый из которых будут производить одинаковый объем продукции?
