1. Определение смешанного произведения, его геометрический смысл
Рассмотрим произведение векторов  ,
,  и
и  , составленное следующим образом: (
, составленное следующим образом: (  х
х  )
)  . Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.
. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.
Выясним геометрический смысл выражения (  х
х  )
)  . Построим параллелепипед, ребрами которого являются векторы
. Построим параллелепипед, ребрами которого являются векторы  ,
,  ,
,  и вектор
и вектор 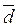 =
=  х
х  (см. рис. 22).
(см. рис. 22).
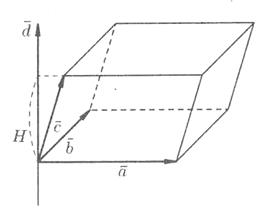
Рис. 22.
Имеем: (  х
х  )
)  =
= 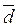 ·
·  = |
= | 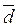 |· пр
|· пр 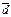
 , |
, | 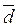 | = |
| = |  х
х  | = S, где S — площадь параллелограмма, построенного на векторах
| = S, где S — площадь параллелограмма, построенного на векторах  и
и  , пр
, пр 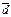
 = Н для правой тройки векторов и пр
= Н для правой тройки векторов и пр 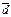
 = -Н для левой, где Н — высота параллелепипеда. Получаем: (
= -Н для левой, где Н — высота параллелепипеда. Получаем: (  х
х  )
)  = S(±H), т. е. (
= S(±H), т. е. (  х
х  )
)  = ±V, где V — объем параллелепипеда, образованного векторами
= ±V, где V — объем параллелепипеда, образованного векторами  ,
,  и
и  .
.
Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
2. Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (  х
х  )
)  = (
= (  х
х  )
)  = (
= (  х
х  )
)  .
.
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. (  х
х  )
)  =
=  (
(  х
х  ).
).
Действительно, (  х
х  )
)  = ±V и
= ±V и  (
(  х
х  ) = (
) = (  х
х  )
)  = ±V. Знак в правой части этих равенств берем один и тот же, так как тройки векторов
= ±V. Знак в правой части этих равенств берем один и тот же, так как тройки векторов  ,
,  ,
,  и
и  ,
,  ,
,  — одной ориентации.
— одной ориентации.
Следовательно, (  х
х  )
)  =
=  (
(  х
х  ). Это позволяет записывать смешанное произведение векторов (
). Это позволяет записывать смешанное произведение векторов (  х
х  )
)  в виде
в виде 

 без знаков векторного, скалярного умножения.
без знаков векторного, скалярного умножения.
3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. 

 = —
= — 

 ,
, 

 = —
= — 

 ,
, 

 = —
= — 

 .
.
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4. Смешанное произведение ненулевых векторов  ,
,  и
и  равно нулю тогда и только тогда, когда они компланарны.
равно нулю тогда и только тогда, когда они компланарны.
Если 

 = 0, то
= 0, то  ,
,  ,
,  — компланарны.
— компланарны.
Допустим, что это не так. Можно было бы построить параллелепипед с объемом V ≠ 0. Но так как 

 = ±V, то получили бы, что
= ±V, то получили бы, что 

 ≠ 0. Это противоречит условию:
≠ 0. Это противоречит условию: 

 = 0.
= 0.
Обратно, пусть векторы  ,
,  ,
,  — компланарны. Тогда вектор
— компланарны. Тогда вектор 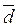 =
=  x
x  будет перпендикулярен плоскости, в которой лежат векторы
будет перпендикулярен плоскости, в которой лежат векторы  ,
,  ,
,  и, следовательно,
и, следовательно, 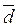 ┴
┴  . Поэтому
. Поэтому 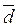 ·
·  = 0, т. е.
= 0, т. е. 

 = 0.
= 0.
3. Выражение смешанного произведения через координаты
Пусть заданы векторы 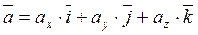 ,
, 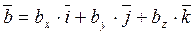 ,
, 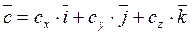 . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
. Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
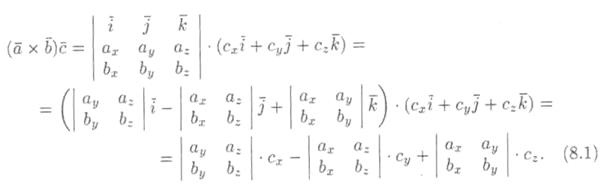
Полученную формулу можно записать короче, так как правая часть равенства представляет собой разложение определителя третьего порядка по элементам третьей строки.
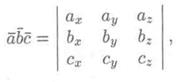
Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
4. Некоторые приложения смешанного произведения
 2015-06-28
2015-06-28 2183
2183
