Конечные и разделённые разности играют особую роль в теории интерполяции. Они используются как для формирования новых интерполяционных формул, так и для оценки погрешности интерполяции.
Пусть дана таблица 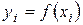 значений функции
значений функции 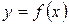 . Конечной разностью первого порядка в точке xi (обозначается символом
. Конечной разностью первого порядка в точке xi (обозначается символом 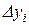 ), называется выражение
), называется выражение
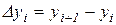 ,
,
второго порядка, обозначается 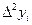 , – выражение
, – выражение
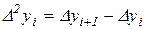 ,
,
k-го порядка, –
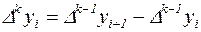 . .
|
Так, например, 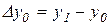 ,
, 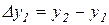 ,
, 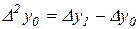
Разделенной разностью первого порядка в точках 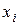 ,
, 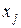 , обозначается
, обозначается 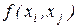 , называется выражение
, называется выражение
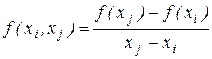 ,
,
второго порядка в точках 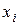 ,
, 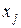 ,
, 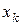 , обозначается
, обозначается 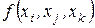 , – выражение
, – выражение
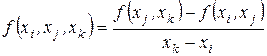 ,
,
k-го порядка в точках 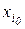 ,
, 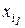 ,
, 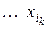 , – выражение
, – выражение
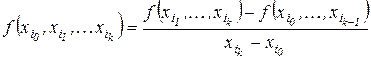 .
.
Так, например,
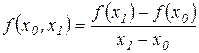 ,
,
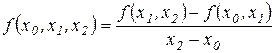 ,
,
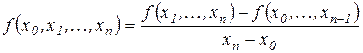 .
.
Получим некоторые полезные для дальнейшего соотношения, связанные с разделенными разностями.
Выразим 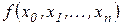 через значения функции в узловых точках. Так, непосредственно из определения следует
через значения функции в узловых точках. Так, непосредственно из определения следует
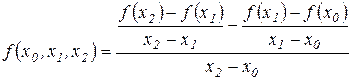 ,
,
и, после очевидных преобразований,
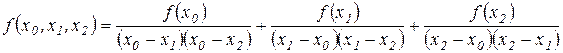 .
.
Продолжая, далее, по индукции, получим
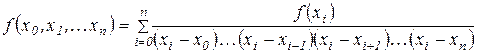 .
.
Или, для сокращения записи, используя функцию 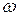 (2.3),
(2.3),
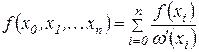 (2.5) (2.5)
|
Замечание. Если в 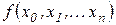 поменять местами значения поменять местами значения 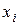 , то это приведет лишь к перестановке соответствующих слагаемых правой части соотношения (2.5). Следовательно, разделенные разности являются симметричными функциями узловых точек. , то это приведет лишь к перестановке соответствующих слагаемых правой части соотношения (2.5). Следовательно, разделенные разности являются симметричными функциями узловых точек.
|
Так, например
|
|
|
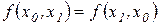 ,
,
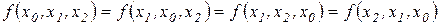 и т.д.
и т.д.
Получим теперь второе полезное соотношение.
Выразим 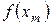 через разделенные разности. Так, непосредственно из определения следует
через разделенные разности. Так, непосредственно из определения следует
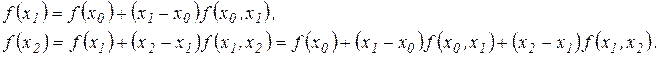
Прибавляя теперь к правой части 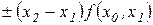 после очевидных преобразований получим
после очевидных преобразований получим
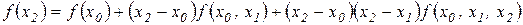 .
.
Рассуждая далее по индукции по m придем к искомому соотношению
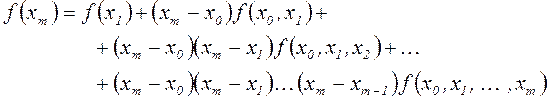 (2.6) (2.6)
|
Если теперь изменить нумерацию точек и обозначить 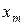 через
через 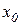 ,
, 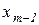 через
через 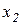 и т.д., то соотношение (2.6) с учетом симметричности распределенных разностей принимает вид
и т.д., то соотношение (2.6) с учетом симметричности распределенных разностей принимает вид
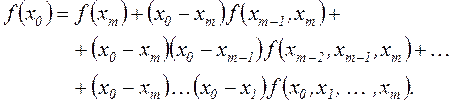 (2.61) (2.61)
|
 2015-06-24
2015-06-24 3050
3050
