Ниже остановимся лишь на основных элементах методики оценки погрешности интерполяционных формул, постараясь сохранить ее логическую схему.
Пусть y=f(x), - интерполируемая функция, а Pn(x)- ее интерполяционный многочлен. Тогда погрешность Rn(x) интерполяции функции в точке х равна
Rn(x)=f(x) – Pn(x),
откуда
f(x)=Pn(x)+Rn(x) (2.8)
Добавим теперь точку x к заданным узловым точкам и рассмотрим интерполяционный многочлен Pn+1(z) в форме Ньютона, построенный уже по (n+2) точкам х0, х1…хn, x. Его значение в точке x равно:
Pn+1(x)=f(x)+(x-x0)f(x0, х1)+...+(х-х0)...(х-хn)f(x0,...хn, х)
Но, по построению, 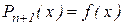 , а первые
, а первые 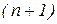 слагаемых правой части представляют собой
слагаемых правой части представляют собой 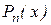 . Таким образом,
. Таким образом,
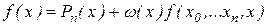 .
.
Сравнивая теперь это соотношение с (2.8),получаем
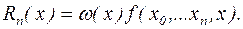 (2.9) (2.9)
|
Это и есть одна из форм представления погрешности аппроксимации. Её недостатком является то обстоятельство, что для вычисления 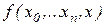 необходимо значение
необходимо значение 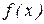 , которое неизвестно. В качестве выхода из такого положения остаётся взять лишь его приближённое значение, т.е.
, которое неизвестно. В качестве выхода из такого положения остаётся взять лишь его приближённое значение, т.е. 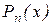 , однако в этом случае соотношение (2.9) становится уже приближённым.
, однако в этом случае соотношение (2.9) становится уже приближённым.
Если же предположить, что функция 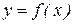 достаточно гладкая и имеет непрерывные производные до
достаточно гладкая и имеет непрерывные производные до 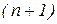 -го порядка включительно, то из формулы
-го порядка включительно, то из формулы
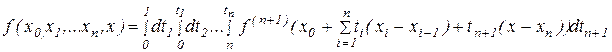 ,
,
справедливость которой следует по индукции, по теореме о среднем вытекает соотношение
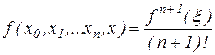 ,
,
где 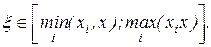 Тогда (2.9) принимает вид
Тогда (2.9) принимает вид
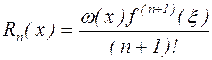 (2.10) (2.10)
|
Недостатком этого соотношения является то, что неизвестно значение 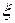 . Однако, если известен вид функции
. Однако, если известен вид функции 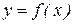 ,то полезной может оказаться оценка
,то полезной может оказаться оценка
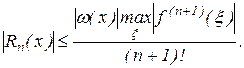
В том случае, когда узловые точки равноотстоящие и 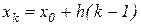 ,
, 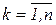 , то по индукции можно показать, что
, то по индукции можно показать, что
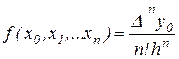 (2.11)
(2.11)
Если к ним добавить точку 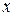 не изменяющую характер расположения узлов, то формула остаётся справедливой и для разделённой разности следующего порядка. Т.е.
не изменяющую характер расположения узлов, то формула остаётся справедливой и для разделённой разности следующего порядка. Т.е.
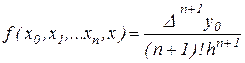 .
.
В противном случае, последнее равенство становится приближённым, и сделав в 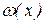 замену
замену 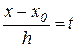 , получим
, получим 
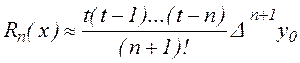 (2.12) (2.12)
|
 2015-06-24
2015-06-24 445
445








