Задание №5
Даны координаты вершин пирамиды
A (12,11,17), B (14,12,14), С(13,14,15), D(12,21,12).
Найти: а) Объем пирамиды б) площадь грани ABC в) Уравнение плоскости, проходящей через точки BCD.
Решение:
Vпир = 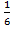 Vпар =
Vпар = 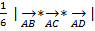
Так как 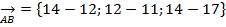 =
= 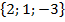
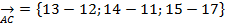 =
= 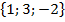
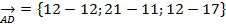 =
= 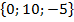
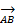 *
* 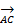 *
* 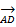 =
= 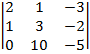 =2
=2 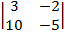 -1
-1 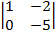 -3
-3 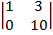 =
=
=2(-15+20)-(-5+0)-3(10*0)=10+5-30=-15
Тогда V пир = 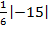 =
= 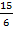 =
= 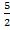 = 2,5 ед3.
= 2,5 ед3.
Площадь грани ABC представляет собой площадь треугольника с вершинами А;B и C. Построим векторы 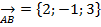 и
и 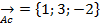 Тогда площадь треугольника ABC равна половине площади параллелограмма, построенного на векторах
Тогда площадь треугольника ABC равна половине площади параллелограмма, построенного на векторах 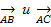 . Т.е. половине длины векторного произведения этих векторов.
. Т.е. половине длины векторного произведения этих векторов.
Найдем:
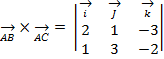 =
= 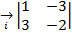 -
- 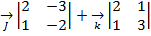 =7
=7 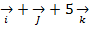
Отсюда 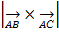 =
= 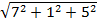 =
= 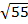
И тогда S 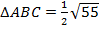
Задание №6
Пирамида ABCD задана координатами своих вершин A(4,-1,0), B(2,3,4), С(-1,4,1), D(4,-3,5).
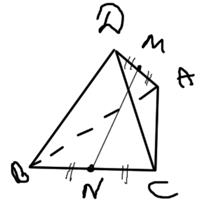
Решение:
1)Найдем координаты вектора MN, если M – середина ребра AD, N – середина ребра BC. Из 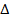 ANC следует, что
ANC следует, что 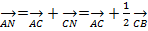
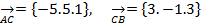
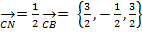 Тогда
Тогда 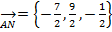
Из 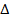 AMN находим:
AMN находим:
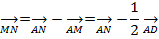
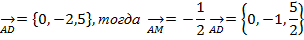
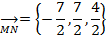
2) Найдем разложение вектора MN по базису AB, AC,AD, если он таковым является. Если AB, AC, AD образуют базис, то они не линейно независимы, т.е. проверм равенство:
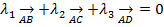
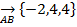 ,
, 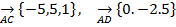
Тогда имеем векторное равенство:
|
|
|
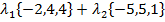 +
+ 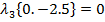 откуда:
откуда:
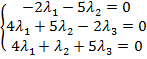
Решим систему уравнений используя метод Гаусса.
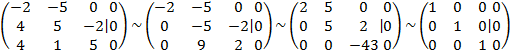
Откуда следует, что система имеет единственное нулевое решение 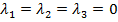
И поэтому векторы 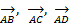 образуют базис.
образуют базис.
Выразим связь между векторами.
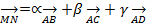
Откуда переходим к системе:
-2 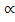 +5
+5 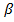 =
= 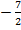
4 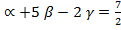
4 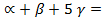 2
2
Решим систему методом Гаусса, получим:
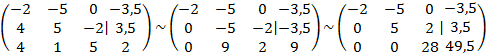
Совершая обратный ход по методу Гаусса, получим:
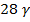 =49,5 5
=49,5 5 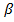 +
+ 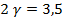
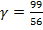 5
5 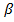 +
+ 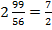
5 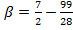 =
= 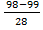 =
= 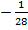
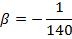
-2 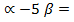 -
- 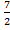
-2 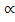 = -
= - 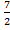 -
- 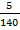 = -
= - 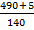
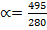 =
= 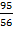
Тогда разложение 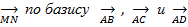 имеет вид:
имеет вид:
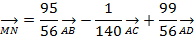
7. задание Составить уравнение плоскости, проходящей через точку М (3, 2, –1) параллельно прямым
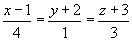 .
.
M1(1;-2;-3) -уже заданная точка по условию задачи, которая принадлежит прямой 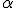
Вектор ММ1{1-3;-2-2;-3-1}={2;-4;-4}
q1{4;1;3} - направляющий вектор прямой 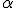 (по условию задачи)
(по условию задачи)
Векторы {x-1;y+2;z+3}, AM1, q1 - компланарны. Поэтому для них можно записать
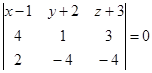
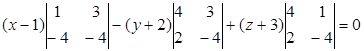
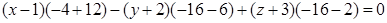
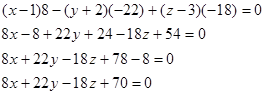
Это и будет искомое уравнение плоскости, которая проходит через точку М и прямую 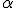
9.задание Привести к каноническому виду уравнение кривой
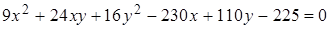 .
.
Решение.
Приводим квадратичную форму
B = 9x2 + 24xy + 16y2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы: 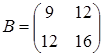
Находим собственные числа и собственные векторы этой матрицы:
(9 - λ)x1 + 12y1 = 0
24x1 + (16 - λ)y1 = 0
Характеристическое уравнение:
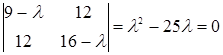
λ2 -25 λ + 0 = 0
D = (-25)2 - 4 • 1 • 0 = 625
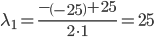
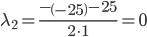
Исходное уравнение определяет параболу (λ2 = 0)
Вид квадратичной формы: 25y12
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B.
λ1 = 0/4
9x1 + 12y1 = 0
12x1 + 16y1 = 0
или
9x1 + 12y1 = 0
Собственный вектор, отвечающий числу λ1 = 0/4 при x1 = 4:
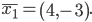
В качестве единичного собственного вектора принимаем вектор: 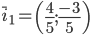
где 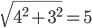 - длина вектора x1. или
- длина вектора x1. или 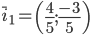
Координаты второго собственного вектора, соответствующего второму собственному числу λ2 = 25, находим из системы:
-16x1 + 12y1 = 0
12x1-9y1 = 0
или
-16x1 + 12y1 = 0
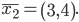
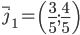
или
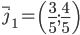
Итак, имеем новый ортонормированный базис (i1, j1).
Переходим к новому базису: 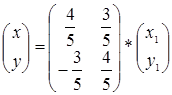
x = 4/5x1 + 3/5y1
y = -3/5x1 + 4/5y1
|
|
|
Вносим выражения x и y в исходное уравнение 9x2 + 24xy + 16y2 - 230x + 110y - 225 и, после преобразований, получаем:
25y21 - 250x1 - 50y1 = 225
Выделяем полные квадраты:
для y1:
25(y12-2•1y1 + 1) -25•1 = 25(y1-1)2-25
Преобразуем исходное уравнение:
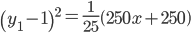
Получили уравнение параболы:
(y - y0)2 = 2p(x - x0)
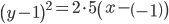
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке (-1;1)
Параметр p = 5
Координаты фокуса:
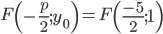
Уравнение директрисы: x = x0 - p/2
x = -1 - 5/2 = - 7/2
11.задание Построить треугольник по периметру 2р, высоте ha и углу В при основании.
Решение:
Нарисуем угол величины α и попробуем отсечь от него прямой BC треугольник ABC, удовлетворяющий двум оставшимся условиям задачи. Это значит, что 1) прямая должна быть удалена от вершины A угла на расстояние ha и 2) периметр треугольника должен равняться 2 p. Ясно, что первое условие выполнено тогда и только тогда, когда прямая касается окружности радиуса ha с центром A. Второе условие определяет аналогичное семейство прямых: все прямые, отсекающие от угла треугольники периметра 2 p, касаются
вписанной в угол окружности, точки касания которой со сторонами угла удалены от его вершины на расстояние p. (Действительно, если обозначить точки касания вневписанной
окружности со сторонами треугольника или их продолжениями, как показано на рисунке, то по теореме об отрезках касательных BC 1= BA 1, CB 1= CA 1. Поэтому сумма отрезков AC 1 и AB 1 равна периметру треугольника, а поскольку эти отрезки по той же теореме равны, каждый из них равен p, а значит вневписанная окружность будет одной и той же для всех рассматриваемых треугольников.) Искомая прямая принадлежит обеим семействам, то есть является общей (внутренней) касательной окружностей. Остается начертить окружности и построить касательную к ним. 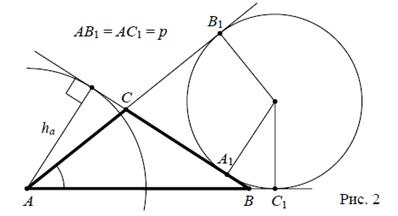
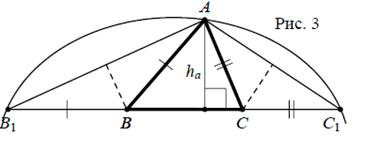
Решение 2: Задачу 2 можно решить и иначе. Допустим, что искомый треугольник ABC построен. Отложим на продолжениях стороны BC отрезки BB 1= BA и CC 1= CA (см. рис. 3). Получился треугольник AB 1 C 1, в котором основание 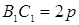 , высота прежняя
, высота прежняя 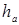 , а угол при вершине А нетрудно найти, пользуясь тем, что треугольники
, а угол при вершине А нетрудно найти, пользуясь тем, что треугольники 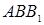 и
и 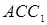 равнобедренные, а их внешние углы при вершинах В и С –это углы при основании треугольника АВС, так что их сумма равна
равнобедренные, а их внешние углы при вершинах В и С –это углы при основании треугольника АВС, так что их сумма равна 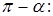
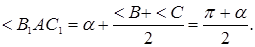
После этого построить треугольник ABC уже просто (точки B и C равноудалены от A, B 1и A, C 1, соответственно).
Название использованного нами метода говорит само за себя – это метод вспомогательной фигуры. Такой фигурой здесь нам послужил треугольник AB 1 C 1.
Очень часто роль вспомогательной фигуры играет фигура, подобная искомой. В этом случае говорят, что используется метод подобия.
14. задание Составить общее уравнение плоскости, проходящей через точку A(3, -4, 1) параллельно координатной плоскости Oxz.
Ax+By+Cz+D=0-Общее уравнение плоскости.
Плоскость параллельная плоскости Oxz имеет вид: By+D=0, так как точка A лежит на этой плоскости, то ее координаты удовлетворяют неравенству: -4В+D=0 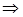 D=4B
D=4B
Подставляем значение в искомое уравнение: 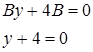 делим на В.
делим на В.
y+4=0- уравнение искомой плоскости.
15. задание Записать уравнение окружности, проходящей через вершины гиперболы 4х2 – 9у2 = 36, и имеющей центр в точке A(0, 4).
Решение:
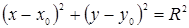
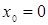 ,
, 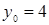
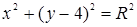
Приведем уравнение гиперболы 4х2 – 9у2 = 36 к каноническому виду:
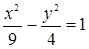
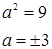
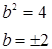

Центр 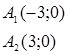
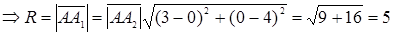
Получаем: 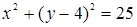
 2015-06-24
2015-06-24 1316
1316






