Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, причем какое именно заранее неизвестно.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями. Этот закон задается в виде таблицы, формулы или графика.
Для дискретных случайных величин одним из наиболее употребительных является так называемый биномиальный закон распределения, к которому приводит схема Бернулли повторения испытаний. Формула (8) и является аналитическим выражением этого закона.
Пример 11.
По каналу связи передается сообщение с помощью кода, состоящего из двух знаков. Вероятность появления первого равна 2/3. Передано три знака. Найти закон распределения для появлений первого знака.
Решение.
По условию n =4, р =2/3, q =1/3. Возможные значения числа появлений первого знака: 0, 1, 2 и 3. Найдем их вероятности по формуле (8):


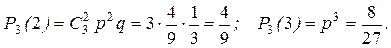
Этот закон можно представить в виде таблицы
| X | ||||
| P1/27 | 1/27 | 2/9 | 4/9 | 8/27 |
Функцией распределения называют функцию, определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньше х, то есть
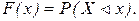 (13)
(13)
Геометрически это означает, что случайная величина с вероятностью р примет значение, которое на числовой оси изображается точкой, лежащей левее х.
Для непрерывной случайной величины функция распределения есть непрерывная кусочно-дифференцируемая функция. Из определения выводятся основные свойства:
1. Значения функции распределения принадлежат отрезку [0,1], т.е.
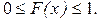
2. F (x) - неубывающая функция, то есть 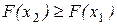 , если
, если 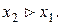
3. Вероятность того, что случайная величина примет значение, заключенное на промежутке [ а,b [, равна приращению функции распределения на этом промежутке
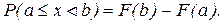 (14)
(14)
Для непрерывной случайной величины вероятность принять отдельное значение равно нулю. Поэтому для непрерывных случайных величин
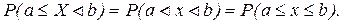
Пример 12.
Случайная величина Х задана функцией распределения
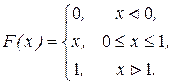
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее отрезку [-1;0,5].
Решение.
Из условия следует, что Х - непрерывная случайная величина, которая может принимать значение от 0 до 1.
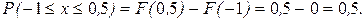
Плотностью распределения вероятностей непрерывной случайной величины Х называют первую производную от функции распределения
 (15)
(15)
Функция распределения F(x) есть одна из первообразных для плотности распределения. Исходя из определения плотности или дифференциального закона распределения и ее связи с функцией распределения, легко показать следующие свойства:
1. Плотность распределения непрерывной случайной величины - неотрицательная функция 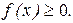
2. Вероятность попадания случайной величины Х в интервал равна
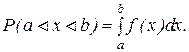 (16)
(16)
3. Из свойства 2 получим выражение для функции распределения
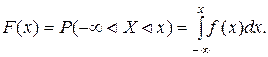 (17)
(17)
4. Условие нормировки
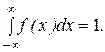 (18)
(18)
Пример 13. Дискретная величина Х задана таблицей
| Х | ||||
| Р | 0,1 | 0,3 | 0,4 | 0,2 |
Найти функцию распределения и построить ее график.
Решение.
1. Если 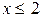 , то
, то 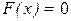 , так как Х не может принимать значение меньше 2.
, так как Х не может принимать значение меньше 2.
2. Пусть 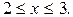
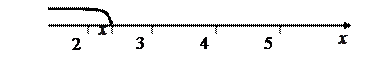

В этом случае в интервал (-¥, х) попадает только одно значение случайной величины Х (X =2). Поэтому
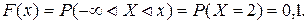
3. Пусть 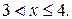
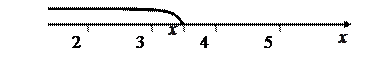

Для любого значения аргумента х функции F(x), удовлетворяющего данному неравенству, в интервал (-¥, х) попадает два значения случайной величины (X =2 и X =3). Поскольку события, что Х примет данные значения являются несовместными (или X =2 или X =3), то
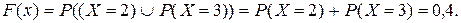
4. Аналогично если 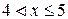
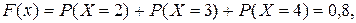
а при 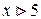
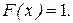
Следовательно, функция распределения будет иметь вид
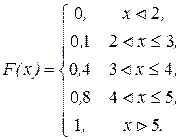
Строим график функции распределения


Рис. 1 - График функции распределения
дискретной случайной величины
Пример 14. Плотность распределения ошибки измерения
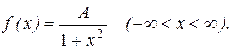
Определить значение коэффициента А и построить график f(x). Найти функцию распределения и построить ее график. Вычислить вероятность того, что ошибка измерения примет значение, заключенное в интервале 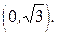
Решение.
Значение коэффициента А легко определить из условия 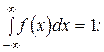
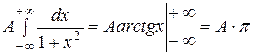 .
.
Приравнивая 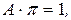 получаем
получаем 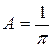 .
.
Функцию распределения F(x) находим по определению
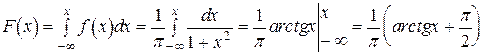 .
.
Вероятность того, что случайная величина попадет в указанный интервал, можно вычислить двумя способами:
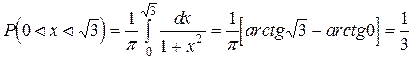
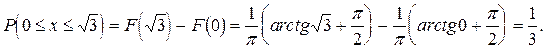
Строим графики функций
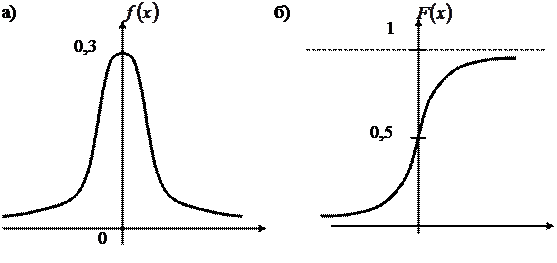

Любой закон распределения случайной величины полностью характеризует ее с вероятностной точки зрения. Однако для практики достаточно бывает указать отдельные числовые характеристики случайной величины, по которым можно судить об особенностях ее распределения. К этим характеристикам относятся среднее или математическое ожидание М (x), дисперсия D (x) и среднее квадратическое отклонение s (x). Две последние величины описывают рассеяние случайной величины относительно среднего.
Для дискретной случайной величины математическое ожидание определяется как сумма произведений всех ее возможных значений на их вероятности.
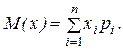 (19)
(19)
Для непрерывной случайной величины:
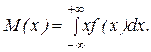 (20)
(20)
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
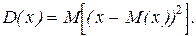 (21)
(21)
Часто бывает удобно пользоваться другой формулой для вычисления дисперсии
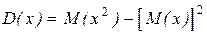 , (22)
, (22)
где 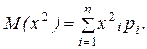 (23)
(23)
для дискретной случайной величины и
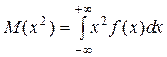 (24) для непрерывной случайной величины.
(24) для непрерывной случайной величины.
Размерность дисперсии равна квадрату размерности случайной величины, что на практике не всегда удобно. Поэтому наряду с дисперсией для характеристики рассеяния используется корень квадратный из дисперсии, называемый средним квадратическим отклонением.
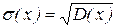 (25)
(25)
Пример 15. Для случайной величины, заданной в примере 11, найти M(x), D(x) и s (x).
Решение
а) В примере 11 закон распределения дискретной случайной величины задан таблицей:
| Х | ||||
| Р | 0,1 | 0,3 | 0,4 | 0,2 |
По формуле (19) получим
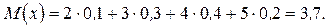
Для определения дисперсии по формуле (22) составим таблицу для случайной величины x2.
| x2 | ||||
| p | 0,1 | 0,3 | 0,4 | 0,2 |
Тогда
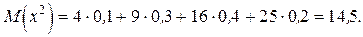
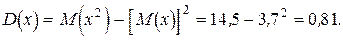
Пример 16. Найти числовые характеристики M(x), D(x), s(x) и постоянную С для равномерно распределенной случайной величины, плотность распределения которой имеет вид:
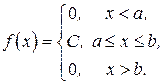
Решение.
Из условия нормировки определим С.
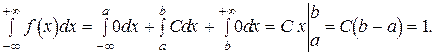
Откуда
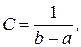
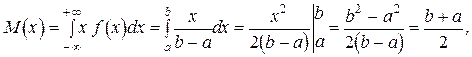
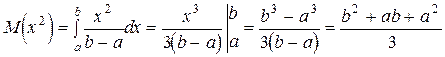 ,
,
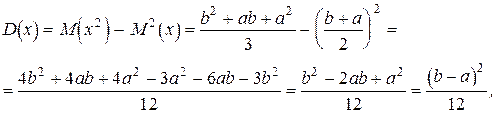
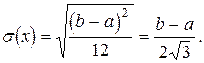
Из всех законов распределения непрерывных случайных величин нормальный закон наиболее часто встречается в практике. Плотность распределения нормального закона может быть записана в виде
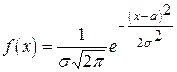 , (26)
, (26)
где s>0 и а — параметры распределения, равные среднему квадратическому отклонению и математическому ожиданию данной случайной величины, соответственно. Вероятность попадания нормально распределенной случайной величины Х в интервал (a,b) вычисляется по формуле
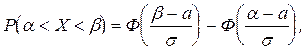 (27)
(27)
где Ф(х) — функция Лапласа (см. формулу (11)).
Вероятность заданного отклонения от математического ожидания можно найти с помощью более простой формулы
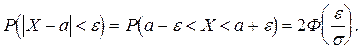 (28)
(28)
Пример 17. Радиолокатор измеряет дальность до цели с систематическими и случайными ошибками. Систематическая ошибка равна 10 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением 25 м. Найти вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 40 м, а также вероятность того, что измеренная дальность не превзойдет истинную.
Решение.
Случайная величина X (ошибка измерения дальности) распределена по нормальному закону.
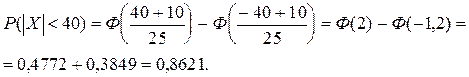
Вероятность того, что измеренная дальность не превзойдет истинную, равна:
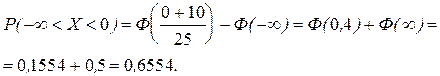
 2015-06-24
2015-06-24 8128
8128
