Название это условное – алгоритм собран из разных кусков.
Склейка – это операция удаления переменной из ДНФ: если входящие в ДНФ ЭК имеют вид K1=xÙK и K2= 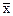 ÙK, то их дизъюнкция: K1Ú K2=(x Ú
ÙK, то их дизъюнкция: K1Ú K2=(x Ú 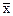 )ÙK=K.
)ÙK=K.
Поглощение – это тождество (равносильность) булевой алгебры: xÙKÚK=K. В результате применения операции поглощения остаётся ЭК, называемая импликантой.
Идея алгоритма – провести все возможные склейки ЭК, затем поглотить лишние ЭК и из остатков найти МДНФ. Очень простая идея алгоритма осложняется тем, что начиная с некоторого шага происходит размножение решений – появляются несколько т.н. тупиковых ДНФ, из которых выбирается МДНФ простым перебором.
1. Первый шаг – получение сокращенной ДНФ.
i) Все точки носителя функции (ЭК) записываются в столбик, сгруппировано по числу единиц (т.е. в антицепь, по слоям сети)
ii) Производятся всевозможные склейки ЭК (естественно, между разными группами). Результат каждой склейки заносится в соседний столбик, а ЭК, вошедшая в склейку, помечается.
|
|
|
iii) Из полученного столбика вычеркиваются повторяющиеся ЭК и добавляются непомеченные ЭК.
iv) Пункты ii) и iii) повторяются, возможно, несколько раз.
v) Результат – сокращенная ДНФ, содержащая импликанты исходной.
2. На втором шаге выделяются ядровые импликанты и тупиковые ДНФ
i) Составляется таблица, в левом столбце которой выписывают импликанты, а в верхней строке – исходные ЭК.
ii) Таблица заполняется следующим образом: на пересечении ставится «+», если соответствующая ЭК поглощается импликантой, в противном случае клетка оставляется пустой.
iii) Заполненная таблица просматривается: ищутся столбцы, содержащие только один «+». Соответствующе «+» импликанты – ядровые, они входят в МДНФ.
iv) Затем из таблицы вычеркиваются сначала строки, содержащие ядровые импликанты, затем столбцы, содержащие «+» от ядровых импликант.
v) Оставшаяся часть таблицы анализируется на предмет выделения тупиковых ДНФ. Принцип следующий: набор импликант каждой тупиковой ДНФ должен покрывать все оставшиеся «+» таблицы.
Из найденных тупиковых ДНФ тривиальным алгоритмом (перебором) выбираются минимальные (их может быть несколько). Дизъюнкции минимальных тупиковых ДНФ с ядровыми импликантами и являются МДНФ (их также может быть не одна).
Пример.
Nf ={0,2,3,6,7}={000,010,100,110,111}, Nf ={1,4,5}={001, 100,101}
| * | 0-0 | ||||||||
| * | * | 01- | 0-0 | + | + | ||||
| * | * | -10 | -1- | + | + | + | + | ||
| * | * | -11 | 11- | ||||||
| * | * | 11- | 01- | ||||||
| * | * | * | * |
Обе получившиеся импликанты – ядровые. Следовательно, МДНФ = 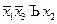
|
|
|
Отступление: геометрический язык – дуальность.
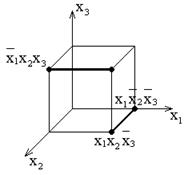
Изобразим носитель функции из примера на булевом кубе размерности 3:
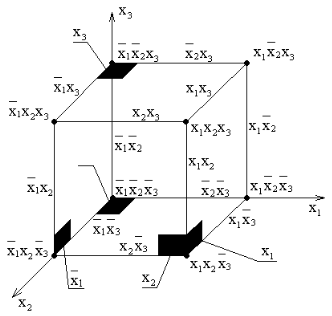
На первом шаге алгоритма склейками получены импликанты, написанные в третьем столбце, общим числом также 5. Они соответствуют соседним ребрам куба. Таким образом, геометрически склейка – это переход от точек куба к покрывающим их рёбрам. Далее, пара ребер также может быть склеена по несущественной переменной, что на геометрическом языке будет обозначать переход к покрытию 2-гранью. Формально это выглядит следующим образом:
Nf ={000}Ç{010}Ç{011}Ç{110}Ç{111}= N1 Ç N2; N1 ={000, 010}, N2 ={010,011,110,111}.
Таким образом, результат минимизации – нахождение покрытия носителя функции ребром и 2-гранью.
Взаимно-однозначное соответствие между точками куба и конституентами единицы очевидным образом продолжается до взаимно-однозначного соответствия между любой импликантой ранга r и гранью размерности n-r, задаваемое формулой:
Проще всего установить это соответствие, дополнив импликанту до полного числа переменных. Соответствующее множество конституент и составит грань куба.
Пример
Т = {(1,0,0), (1,1,0), (1,1,1), (0,1,1)}.
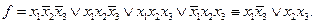
Теперь можно дать точную формулировку задаче минимизации булевой функции на геометрическом языке: для данного множества Nf найти его покрытие минимальным числом граней максимальной размерности: Nf = N1 Ç N2 Ç…
Так им образом, на геометрическом языке процедуре минимизации булевых функций соответствует нахождение минимального покрытия носителя функции. Минимального в смысле покрытия множества – носителя гранями максимальной размерности. Максимальной грани соответствуют простые импликанты. Теоретико-множественному объединению максимальных граней будет соответствовать дизъюнкция простых импликант, т.е., сокращённая ДНФ. Поиску ядровых и тупиковых ДНФ соответствует нахождение минимальных покрытий носителя функции.
 2015-06-24
2015-06-24 2023
2023