Элементы теории вероятности
Пусть ξ – одномерная случайная величина, которая может принимать различные значения на (−∞,+∞).
Функция распределения F случайной величины ξ есть вероятность P того, что ξ < x:
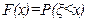 .
.
Вероятность того, что 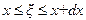 есть дифференциал
есть дифференциал
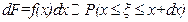
где 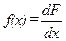 − плотность распределения вероятности.
− плотность распределения вероятности.
Математическая ожидание случайной величины ξ есть величина:
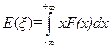
Таким образом, математическое ожидание некоторой физической величины Ψ (ξ) выражается как:
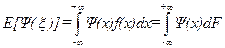
Дисперсия случайной величины ξ вычисляется по формуле:
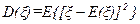
Среднеквадратичное отклонение случайной величины ξ:
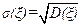
Многомерное распределение вероятностей
Пусть некоторое случайное событие описывается действительными числами ξ 1 ,…, ξ n, которые могут принимать различные значения от −∞ до +∞ и образуют случайный вектор ξ ={ ξ 1 ,…, ξ n}. В этом случае говорят об n-мерном распределении вероятностей получения различных значений x ={ x 1 ,…, x n} вектора ξ. Оно характеризуется функцией распределения 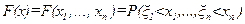 .
.
Плотность распределения вероятностей случайного вектора ξ вычисляется по формуле:
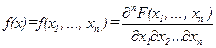
Математическое ожидание случайного вектора ξ представляет собой вектор:
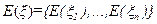
Ковариационная матрица случайного вектора ξ имеет вид:
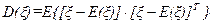
или в матричном виде:
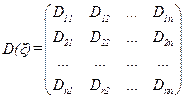
где диагональные элементы есть дисперсии соответствующих составляющих вектора ξ:
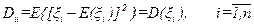
а недиагональные элементы 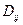 называются ковариациями (корреляционными моментами):
называются ковариациями (корреляционными моментами):
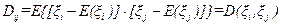
Очевидно, что 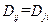 , т.е. любая ковариационная матрица симметрична. Величины
, т.е. любая ковариационная матрица симметрична. Величины
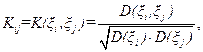
называются коэффициентами корреляции между ξ i и ξ j, причем 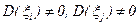 .
.
Две случайные величины ξ i и ξ j, для которых 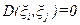 (т.е.
(т.е. 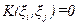 ) называются взаимно некоррелированными.
) называются взаимно некоррелированными.
Если все составляющие вектора ξ ={ ξ 1 ,…, ξ n} взаимно не коррелированны, то вектор ξ называется некоррелированным. Его ковариационная матрица является диагональной:
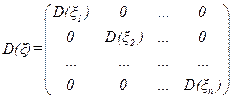
Если 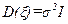 , где
, где 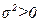 некоторое число, а I – единичная матрица, то вектор ξ называется некоррелированным равноточным. Случайные величины ξ i и ξ j, называются независимыми, если плотность распределения
некоторое число, а I – единичная матрица, то вектор ξ называется некоррелированным равноточным. Случайные величины ξ i и ξ j, называются независимыми, если плотность распределения 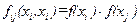 . Все составляющие вектора ξ независимы в совокупности, если любая пара их взаимно независима. Для этого необходимо и достаточно, что бы
. Все составляющие вектора ξ независимы в совокупности, если любая пара их взаимно независима. Для этого необходимо и достаточно, что бы 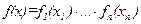 .
.
Если две случайные величины взаимно независимы, то они некоррелированны. Однако, обратное утверждение не имеет смысла.
Если ранг ковариационной матрицы 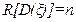 , то распределение вектора ξ называется собственным и сам вектор ξ –собственный, а при
, то распределение вектора ξ называется собственным и сам вектор ξ –собственный, а при 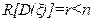 – несобственным.
– несобственным.
Легко доказать, что любой собственный случайный вектор ξ может быть преобразован в некоторый некоррелированный равноточный вектор η.
Нормальное многомерное распределение вероятностей случайного вектора ξ ={ ξ 1 ,…, ξ n} имеет плотность распределения:
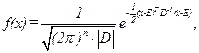
где 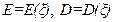 – математическое ожидание и ковариационная матрица вектора ξ.
– математическое ожидание и ковариационная матрица вектора ξ.
Свойства нормального распределения:
1) Нормальное распределение полностью определяется математическим ожиданием Е и ковариационной матрицей D рассматриваемого случайного вектора.
2) Максимум плотности этого распределения достигается в точке 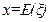 (в точке среднего значения случайной величины).
(в точке среднего значения случайной величины).
3) При любом разбиении ξ ={ ξ 1 ,…, ξ k} распределенного вектора ξ ={ ξ 1 ,…, ξ n} на несколько частей, эти части ξj (j=1,2,…,k) распределены нормально.
4) Составляющие ξ 1 ,…, ξ n любого нормально распределенного некоррелированного вектора ξ независимы в совокупности, т.е. удовлетворяют условию 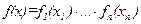 (т.е. составляющие вектора ξ независимы в совокупности, если любая пара их взаимно независима).
(т.е. составляющие вектора ξ независимы в совокупности, если любая пара их взаимно независима).
5) Любая (векторная или скалярная) линейная функция с неслучайными коэффициентами от составляющих нормально распределенного вектора также распределена нормально.
6) Путем линейного преобразования 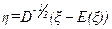 можно привести любое нормальное распределение к простейшему виду:
можно привести любое нормальное распределение к простейшему виду: 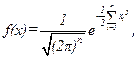
Распределений Лапласа для некоторого случайного вектора ξ, составляющие которого независимы в совокупности, имеет плотность распределения:
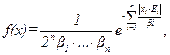
где 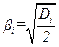 , а Ei и Di (i =1,…,n) – математические ожидания и дисперсии соответствующих составляющих вектора ξ.
, а Ei и Di (i =1,…,n) – математические ожидания и дисперсии соответствующих составляющих вектора ξ.
Свойства математических ожиданий и дисперсий:
E(Aξ)=AE(ξ)
E(ξ+a)=E(ξ)+a
D(Aξ)=AD(ξ)AT
D(ξ+a)=D(ξ)
где A – неслучайная матрица, a – неслучайный вектор, ξ – случайный вектор.
 2015-06-26
2015-06-26 950
950






