49. Цилиндрические поверхности: определение, вывод уравнения, примеры.
Пусть Г – линия и 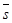 - ненулевой вектор, не параллельный плоскости линии Г (если Г плоская линия.
- ненулевой вектор, не параллельный плоскости линии Г (если Г плоская линия.
Определение 36. Цилиндрической поверхностью с направляющей Г и образующими, параллельными вектору 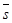 , называется множество точек всех возможных прямых, параллельных вектору
, называется множество точек всех возможных прямых, параллельных вектору 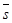 и пересекающих линию Г.
и пересекающих линию Г.
Основная задача, которую нужно решить: как найти уравнение цилиндрической поверхности, если даны уравнения линии Г и координаты вектора 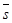 .
.
Пусть в пространстве введена АСК, 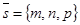 и линия Г имеет уравнения
и линия Г имеет уравнения 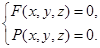 (85) Обозначим цилиндрическую поверхность Ц.
(85) Обозначим цилиндрическую поверхность Ц.
М Î Ц Û (М Î l, где l || 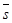 и l Ç Г ¹ Æ).
и l Ç Г ¹ Æ).
Обозначим l Ç Г = N. Если N(х0, у0, z0), то 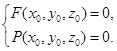 (*) Если М(х, у, z), то М Î Ц Û х = х0 + mt, у = у0 + nt, z = z0 + рt, где t Î R. Отсюда х0 = х - mt, у0 = у - nt, z0 = z - рt. Подставив х0, у0, z0 в равенства (*), получим
(*) Если М(х, у, z), то М Î Ц Û х = х0 + mt, у = у0 + nt, z = z0 + рt, где t Î R. Отсюда х0 = х - mt, у0 = у - nt, z0 = z - рt. Подставив х0, у0, z0 в равенства (*), получим
уравнения Ц. 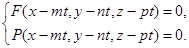 (86)
(86)
Остаётся из этих уравнений исключить параметр t.
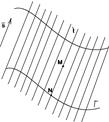
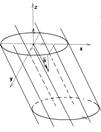
Рис. 78 Рис.79
Получили следующие правила для составления уравнения цилиндрической поверхности:
|
|
|
Если направляющая цилиндрической поверхности задаётся уравнениями (85) и образующие параллельны вектору 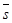 , то для составления уравнения поверхности достаточно в уравнениях (85) заменить х на х - mt, у на у - nt, z на z - рt и из полученных уравнений исключит параметр.
, то для составления уравнения поверхности достаточно в уравнениях (85) заменить х на х - mt, у на у - nt, z на z - рt и из полученных уравнений исключит параметр.
Пример 1. Составьте уравнение цилиндрической поверхности, если образующие параллельны вектору 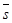 = {3, 2, -1} и направляющая Г имеет уравнения
= {3, 2, -1} и направляющая Г имеет уравнения 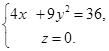
Решение. Линия Г – эллипс в плоскости (ХОУ) с полуосями 3 и 2 (рис. 79). В уравнениях линии Г заменяем х на х - 3t, у на у - 2t, z на z + t.
Получим 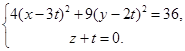

Из второго уравнения t = - z. Подставим в первое уравнение. 4(х + 3z)2 + 9(у + 2z)2 = 36. Раскрыв скобки и приведя подобные, получим
4х2 + 9у2 + 72z2 + 24хz + 36уz - 36 = 0.
Это уравнение данной цилиндрической поверхности.
Пример 2. Составьте уравнение цилиндрической поверхности, если направляющей является линия 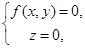 лежащая в плоскости (ХОУ), а образующие параллельны оси (ОZ).
лежащая в плоскости (ХОУ), а образующие параллельны оси (ОZ).
Решение. Вектор, параллельный образующим, есть вектор 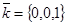 . Заменяем в уравнениях направляющей х на х - 0•t, т.е. х заменяем на х. Аналогично, у заменяем на у. Но z заменяем на z - t. Получим
. Заменяем в уравнениях направляющей х на х - 0•t, т.е. х заменяем на х. Аналогично, у заменяем на у. Но z заменяем на z - t. Получим 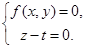 Из второго уравнения z = t. Это значит, что z может независимо от х и у принимать все возможные действительные значения, а х и у связаны тем же уравнением f(х, у) = 0, что и в уравнении направляющей. Уравнение цилиндрической поверхности в этом случае будет f(х, у) = 0.
Из второго уравнения z = t. Это значит, что z может независимо от х и у принимать все возможные действительные значения, а х и у связаны тем же уравнением f(х, у) = 0, что и в уравнении направляющей. Уравнение цилиндрической поверхности в этом случае будет f(х, у) = 0.
Следствие. Уравнения 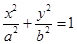 ,
, 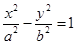 , у2 = 2рх задают цилиндрические поверхности с направляющими эллипсом, гиперболой и параболой соответственно. Их образующие параллельны оси (ОZ).
, у2 = 2рх задают цилиндрические поверхности с направляющими эллипсом, гиперболой и параболой соответственно. Их образующие параллельны оси (ОZ).
Если направляющая цилиндрической поверхности есть линия второго порядка, то поверхность называется цилиндром второго порядка.
|
|
|
Замечание. Обратите внимание на то, что уравнения f(х, у) = 0, f(х, z) = 0, f(у, z) = 0, задают на плоскостях (ХОУ), (ХОZ) и (УОZ) соответственно некоторые линии. Но в аффинной системе координат в пространстве они задают цилиндры с образующими, параллельными оси (ОZ), (ОУ) и (ОХ) соответственно.
50. Конические поверхности: определение, вывод уравнения, примеры.
Определение 37. Конической поверхностью с направляющей Г и вершиной S (S и Г не лежат в одной плоскости) называется множество точек всех возможных прямых, проходящих через S и пересекающих Г.
Коническую поверхность обозначим К. Прямые, на которых лежат все точки К, называются образующими.
Пусть в пространстве зафиксирована система аффинных координат, S(х0, у0, z0), Г: 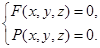
М Î К Û М лежит хотя бы на одной из образующих. Пусть М Îq. Каждая образующая пересекает линию Г. Пусть Г Ç q = N (рис. 64). Если N(х1, у1, z1), то 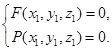 (*)
(*)
Прямая q проходит через две точки, N и S, М Î q Û х = х0 + (х1 – х0)×t, у = у0 + (у1 – у0)×t, z = z0 + (z1 - z0)×t, tÎR. И этих равенств х1 = 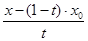 , у1 =
, у1 = 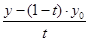 ,
, 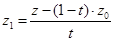 .
.
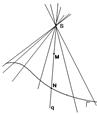
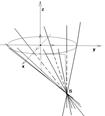
Рис. 80 Рис.81
Подставив х1, у1, z1 в систему (*), получим уравнения данной конической поверхности, но эти уравнения содержат параметр t. Для того, чтобы получить общее уравнение К, нужно из полученной системы исключить параметр t.
Получили следующие правила для составления уравнения конической поверхности:
Для составления уравнения поверхности К достаточно в уравнениях направляющей заменить х на 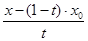 , у на
, у на 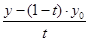 , z на
, z на 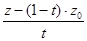 и из полученной системы исключить параметр t.
и из полученной системы исключить параметр t.
Пример 3. Найдите уравнение конической поверхности с вершиной S(2, 2, -3), если
направляющей является эллипс 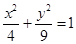 , z = 0.
, z = 0.
Решение. В уравнениях эллипса заменимх на 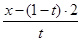 , у на
, у на 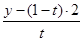 , z на
, z на 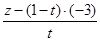 . Получим
. Получим 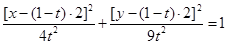 ,
, 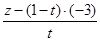 = 0. Найдём из второго уравнения t, получим t =
= 0. Найдём из второго уравнения t, получим t = 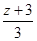 . Подставив в первое уравнение, получим 81х2 +36у2 - 272z2 +108хz - 48уz - 288у - 1752 z - 2340 =0.
. Подставив в первое уравнение, получим 81х2 +36у2 - 272z2 +108хz - 48уz - 288у - 1752 z - 2340 =0.
Замечание. Если направляющей является линия второго порядка, то полученная поверхность называется конусом второго порядка. Можно показать, что для любого конуса второго порядка можно в качестве направляющей взять эллипс, поэтому конус второго порядка называют эллиптическим конусом.
51. Поверхности вращения: определение, вывод уравнения, примеры.
Пусть даны линия Г и прямая р.
Определение 38.Поверхностью, полученной вращением линии Г вокруг оси р, называется множество точек всех возможных окружностей, лежащих в плоскостях, перпендикулярных р, центры которых лежат на р и которые пересекают линию Г.
Выведем уравнение поверхности вращения в том случае, когда Г и р лежат в одной плоскости (обозначим эту плоскость П). Выберем прямоугольную систему координат, направив ось (ОХ) по оси р, ось (ОУ) – в плоскости П, тогда ось (ОZ) будет перпендикулярна П.
Так как линия Г лежит в плоскости (ХОУ), то в этой плоскости она задаётся некоторым уравнением f(х, у) = 0 (*).
Пусть М(х, у, z) – произвольная точка. Тогда
М Î поверхности вращения Û М Î w,
где w - окружность, центр С которой лежит на оси (ОХ), её плоскость перпендикулярна оси (ОХ) и радиус равен ½NС½ (N Î Г). Тогда точка С(х, 0, 0), N(х, у1, 0), ½NС½ = ½у1½, ½МС½= 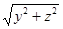 . Следовательно,
. Следовательно,
М Î w Û 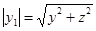 Û у1 = ±
Û у1 = ± 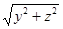 .
.
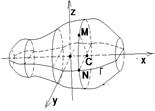
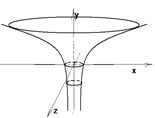
Рис. 82 Рис.83
Так как N Î Г, то f(х, у1) = 0. Подставив значение у1, получим f(х, ± 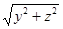 ) = 0 (87). Это и есть уравнение данной поверхности вращения. Итак, получили следующее правило:
) = 0 (87). Это и есть уравнение данной поверхности вращения. Итак, получили следующее правило:
Если линия Г лежит в плоскости (ХОУ) и ось вращения совпадает с осью (ОХ), то для того, чтобы получить уравнение поверхности вращения, достаточно в уравнении линии Г координату х оставить без изменения, а у заменить на ± 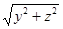 .
.
Пример 4. Написать уравнение поверхности, образованной вращением линии у = logx вокруг оси (ОУ).
Решение. Так как линия Г лежит в плоскости (ХОУ) и осью вращения является ось (ОУ) то в уравнении у = logx нужно у оставить без изменения, а х заменить на 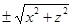 . Так как логарифм отрицательного числа не существует, то х заменяем на
. Так как логарифм отрицательного числа не существует, то х заменяем на 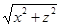 . Получим уравнение
. Получим уравнение 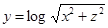 .
.
|
|
|
52. Эллипсоиды: определение, исследование методом сечений.
Определение 39. Эллипсоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением
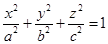 (88)
(88)
Из уравнения сразу следуют такие свойства эллипсоида:
Возможны случаи:
1) -с < h < с. В этом случае система (*) определяет эллипс в плоскости z = h. Полуоси эллипса равны а 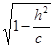 и b
и b 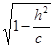 . Наибольшие полуоси получаются при h = 0, т.е. в плоскости (ХОУ). При h ® ± с полуоси стремятся к нулю, т.е. эллипс стягивается в точку.
. Наибольшие полуоси получаются при h = 0, т.е. в плоскости (ХОУ). При h ® ± с полуоси стремятся к нулю, т.е. эллипс стягивается в точку.
2) h = ± с. В каждой из этих плоскостей система (*) определяет точку, т.е. плоскости z = ± с пересекают эллипсоид в одной точке каждая (рис.84).3) h > с или h < -с. В этом случае система (*) определяет пустое множество точек, т.е. плоскости z = h при указанных h не пересекают эллипсоид.
II. При пересечении эллипсоида плоскостями, параллельными (ХОZ) и (УОZ) получим аналогичные результаты. Проведите эти исследования самостоятельно.
- а £ х £ а, - b £ у £ b, -с £ z £ с. Следовательно, эллипсоид лежит внутри прямоугольного параллелепипеда, симметричного относительно координатных плоскостей, длины рёбер которого равны 2 а, 2 b, 2 с;
Эллипсоид симметричен относительно координатных плоскостей, координатных осей и начала координат.
Исследуем форму эллипсоида.
Если поверхность задана уравнением, то исследование её формы часто бывает удобно проводить методом сечений. Для этого исследуемую поверхность пересекают различными плоскостями, проще всего координатными и параллельными координатным.
I. Пересечём эллипсоид плоскостью, параллельной (ХОУ), её уравнение z = h. Уравнения сечения будут 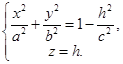 (*)
(*) 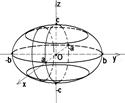 Рис. 84
Рис. 84
53. Однополостный гиперболоид: определение, исследование методом сечений.
Определение 40. Однополостным гиперболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением
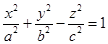 (89)
(89)
Из уравнения (89) следует
|
|
|
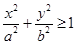 , т.е. гиперболоид лежит вне эллиптического цилиндра, образующие которого параллельны оси (ОZ);
, т.е. гиперболоид лежит вне эллиптического цилиндра, образующие которого параллельны оси (ОZ);
Однополостный гиперболоид симметричен относительно координатных плоскостей, координатных осей и начала координат.
Исследуем форму этого гиперболоида методом сечений.
I. Пересечём гиперболоид плоскостью, параллельной (ХОУ), её уравнение z = h. Уравнения сечения будут 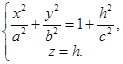 (**)
(**)
При любом h это уравнение определяет эллипс с полуосями а 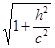 и b
и b 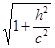 . Наименьший эллипс получается при h = 0, т.е. в плоскости (ХОУ). При возрастании ½h½ полуоси эллипсов увеличиваются и стремятся к бесконечности (рис. 85).
. Наименьший эллипс получается при h = 0, т.е. в плоскости (ХОУ). При возрастании ½h½ полуоси эллипсов увеличиваются и стремятся к бесконечности (рис. 85).
II. При пересечении гиперболоида плоскостями у = m, параллельными плоскости (УОZ). Уравнения сечений
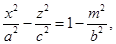 у = m. (***)
у = m. (***)
Возможны случаи:
1) -b < m < b. Сечениями будут гиперболы, действительные оси которых параллельны оси (ОХ) и полуоси имеют длину а 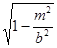 и b
и b 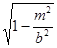 . Наибольшие полуоси получаются при m = 0. При увеличении ½m½ полуоси уменьшаются и стремятся к нулю. Следовательно, ветви гиперболы сближаются.
. Наибольшие полуоси получаются при m = 0. При увеличении ½m½ полуоси уменьшаются и стремятся к нулю. Следовательно, ветви гиперболы сближаются.
2)½m½ = b. В этом случае 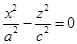 . Это уравнение определяет пару пересекающихся прямых. Итак, плоскости у = b и у = -b пересекают каждая гиперболоид по паре пересекающихся прямых.
. Это уравнение определяет пару пересекающихся прямых. Итак, плоскости у = b и у = -b пересекают каждая гиперболоид по паре пересекающихся прямых.
3) ½m½ > b. В этом случае уравнения (***) определяют гиперболу,действительная ось которой параллельна оси (ОZ). При увеличении ½m½ полуоси будут возрастать, следовательно, ветви гиперболы удаляются друг от друга (рис. 69).
III. При пересечении гиперболоида плоскостями х = n, параллельными плоскости (УОZ) получим результаты, аналогичные результатам предыдущего пункта (проведите это исследование сами).
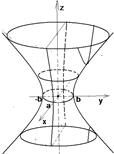
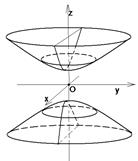
Рис. 85 Рис. 86
54. Двуполостный гиперболоид.
Определение 41. Двуполостным гиперболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением
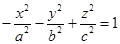 (90)
(90)
Из уравнения (90) следует
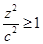 , т.е. гиперболоид лежит вне полосы, ограниченной плоскостями z = ± с.
, т.е. гиперболоид лежит вне полосы, ограниченной плоскостями z = ± с.
Однополостный гиперболоид симметричен относительно координатных плоскостей, координатных осей и начала координат.
Исследуем форму этого гиперболоида методом сечений.
I. Пересечём гиперболоид плоскостью, параллельной (ХОУ), её уравнение z = h. Уравнения
сечения 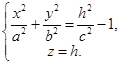 (*).
(*).
Как отмечено выше, плоскости z = h при -с < h < с не пересекают гиперболоид. При ½h½ > с в сечении получается эллипс с полуосями 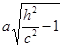 и
и 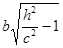 . Эти полуоси неограниченно возрастают при увеличении ½h½.
. Эти полуоси неограниченно возрастают при увеличении ½h½.
II. При пересечении гиперболоида плоскостями у = m, параллельными плоскости (ХОZ) получаются линии
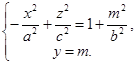 Эти уравнения определяют гиперболы, полуоси которых возрастают при увеличении ½m½.
Эти уравнения определяют гиперболы, полуоси которых возрастают при увеличении ½m½.
III. При пересечении гиперболоида плоскостями, параллельными плоскости (УОZ) получаются тоже гиперболы Исследуйте этот случай сами) (рис. 86).
55. Эллиптический и гиперболический параболоиды.
Определение 42. Эллиптическим параболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением 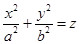 (91).
(91).
Из уравнения (91) следует:
z ³ 0, т.е. параболоид лежит целиком в одной полуплоскости с границей (ХОУ), а именно в той, в которой лежит положительная полуось ОZ;
параболоид симметричен относительно плоскостей (ХОZ), (УОZ) и оси (ОZ).
Исследуем параболоид методом сечений. Очевидно плоскости z = h могут пересекать параболоид только при h ³ 0. при этом в сечениях будут получаться эллипсы с полуосями
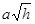 и
и 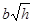 , если h > 0. Эти полуоси неограниченно возрастают при увеличении h. При h = 0 в сечении будет одна точка – начало координат.
, если h > 0. Эти полуоси неограниченно возрастают при увеличении h. При h = 0 в сечении будет одна точка – начало координат.
Плоскости, параллельные плоскостям (ХОZ) и (УОZ), пересекают параболоид по параболам (исследуйте эти сечения самостоятельно) (рис. 87).
Определение 43. Гиперболическим параболоидом называется множество точек пространства, которое в некоторой прямоугольной системе координат можно задать уравнением 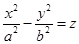 (92).
(92).
Из уравнения (92) следует, что параболоид симметричен относительно плоскостей (ХОZ), (УОZ) и оси (ОZ).
Исследуем параболоид методом сечений.
I. При пересечении параболоида плоскостями z = h, параллельными плоскости (ХОУ), получаются линии 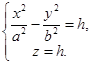 (*)
(*)
При h < 0 в сечении получаются гиперболы, действительные оси которых параллельны оси (ОУ), при h > 0 -гиперболы с действительными осями, параллельными оси (ОХ). При h = 0 плоскость (ХОУ) пересекает параболоид по паре пересекающихся прямых.
II. В сечении плоскостями у = m, параллельными плоскости (ХОZ) получаются параболы 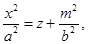 у = m, оси которых параллельны оси (ОZ), ветви направлении в направлении оси (ОZ) и вершинами являются точки (0, m,
у = m, оси которых параллельны оси (ОZ), ветви направлении в направлении оси (ОZ) и вершинами являются точки (0, m, 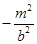 ).
).
III. В сечении плоскостями х = n, параллельными плоскости (УОZ), получаются линии 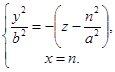 Эти уравнения определяют параболы, оси которых параллельны оси (ОZ), ветви направлении в направлении, противоположном оси (ОZ), и вершинами являются точки (n, 0,
Эти уравнения определяют параболы, оси которых параллельны оси (ОZ), ветви направлении в направлении, противоположном оси (ОZ), и вершинами являются точки (n, 0, 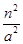 ).
).
Исследование методом сечений даёт следующую поверхность
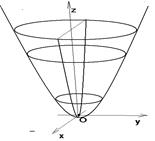
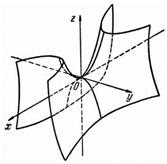
Рис. 87
56. Прямолинейные образующие поверхности. Вывод уравнений прямолинейных образующих однополостного гиперболоида и гиперболического параболоида.
Определение 43. Прямая называется прямолинейной образующей поверхности, если она целиком лежит на поверхности.
Очевидно, любая плоскость имеет бесконечно много прямолинейных образующих. Цилиндрические и конические поверхности, согласно их определению, тоже имеют бесконечно много прямолинейных образующих. Эллипсоид не может иметь прямолинейных образующих, т.к. он заключён внутри параллелепипеда.
Теорема 1. Эллиптический параболоид не имеет прямолинейных образующих.
Доказательство. Пусть q: 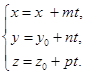 Прямая q будет целиком лежать на эллиптическом параболоиде, заданном уравнением (91), тогда и только тогда, когда
Прямая q будет целиком лежать на эллиптическом параболоиде, заданном уравнением (91), тогда и только тогда, когда
уравнение 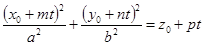 удовлетворяется при любом значении t. Преобразовав его, получим
удовлетворяется при любом значении t. Преобразовав его, получим 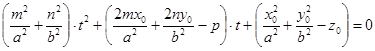 . Этому уравнению удовлетворяет любое действительное число t тогда и только тогда, когда все его коэффициенты равны нулю, т.е.
. Этому уравнению удовлетворяет любое действительное число t тогда и только тогда, когда все его коэффициенты равны нулю, т.е. 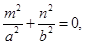
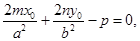
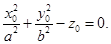 Отсюда следует, что m = n =р = 0, что невозможно, ибо m, n, р – координаты направляющего вектора прямой. Итак, никакая прямая не может целиком лежать на эллиптическом параболоиде.
Отсюда следует, что m = n =р = 0, что невозможно, ибо m, n, р – координаты направляющего вектора прямой. Итак, никакая прямая не может целиком лежать на эллиптическом параболоиде.
Теорема 2. Двуполостный гиперболоид не имеет прямолинейных образующих.
Доказательство аналогично доказательству теоремы 1, проведите его самостоятельно.
Теорема 3. Однополостный гиперболоид имеет два бесконечных семейства прямолинейных образующих.
Доказательство. Пусть гиперболоид задан уравнением 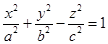 . Отсюда
. Отсюда 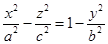 , или
, или 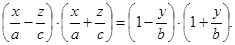 Это уравнение, а следовательно и данное уравнение эквивалентно как уравнению
Это уравнение, а следовательно и данное уравнение эквивалентно как уравнению 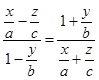 (*), так и уравнению
(*), так и уравнению 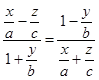 (**). Обозначая в (*) каждую дробь через a, получим, что уравнение (*), а поэтому и уравнение гиперболоида, эквивалентно системе
(**). Обозначая в (*) каждую дробь через a, получим, что уравнение (*), а поэтому и уравнение гиперболоида, эквивалентно системе 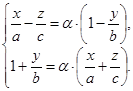 Но эта система есть общие уравнения прямой. Так как a - любое действительное число, то получили бесконечное множество прямых, целиком покрывающих гиперболоид. Через каждую точку гиперболоида проходит точно одна из таких прямых.
Но эта система есть общие уравнения прямой. Так как a - любое действительное число, то получили бесконечное множество прямых, целиком покрывающих гиперболоид. Через каждую точку гиперболоида проходит точно одна из таких прямых.
Обозначая в (**) каждую дробь через b, получим, что уравнение (**), а поэтому и уравнение гиперболоида, эквивалентно системе 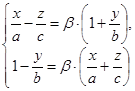 Но эта система есть общие уравнения прямой. Так как b - любое действительное число, то получили бесконечное множество прямых, целиком покрывающих гиперболоид. Через каждую точку гиперболоида проходит точно одна из таких прямых. Очевидно первое и второе множества прямых – различные.
Но эта система есть общие уравнения прямой. Так как b - любое действительное число, то получили бесконечное множество прямых, целиком покрывающих гиперболоид. Через каждую точку гиперболоида проходит точно одна из таких прямых. Очевидно первое и второе множества прямых – различные.
Итак, на однополостном гиперболоиде укладываются два бесконечных семейства прямолинейных образующих.
Теорема 4. На гиперболическом параболоиде лежат два бесконечных семейства прямолинейных образующих.
Доказательство. Уравнение (38) можно преобразовать к виду
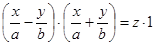 .
.
Это уравнение эквивалентно как уравнению 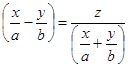 (*), так и уравнению
(*), так и уравнению 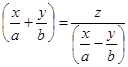 (**). Уравнение (*) эквивалентно системе
(**). Уравнение (*) эквивалентно системе 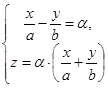 . При любом a эта система задаёт прямую. Получили семейство прямых, целиком покрывающих параболоид. Через каждую точку параболоида проходит точно одна прямая этого семейства. Уравнение (**) эквивалентно системе
. При любом a эта система задаёт прямую. Получили семейство прямых, целиком покрывающих параболоид. Через каждую точку параболоида проходит точно одна прямая этого семейства. Уравнение (**) эквивалентно системе 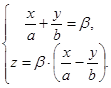 Получили второе семейство прямых, целиком покрывающих параболоид. Через каждую точку параболоида проходит точно одна прямая этого семейства.
Получили второе семейство прямых, целиком покрывающих параболоид. Через каждую точку параболоида проходит точно одна прямая этого семейства.
Итак, на поверхности гиперболического параболоида лежат два бесконечных семейства прямолинейных образующих.
Пример 5. Найдите прямолинейные образующие гиперболического параболоида
Х2 - 4 У 2 = Z,
проходящие через точку М (-1, 2, -15).
Решение. Так как координаты точки М удовлетворяют данному уравнению, то эта точка лежит на данном параболоиде. Запишем уравнение в виде (Х - 2 У)(Х + 2 У) = Z× 1, получим две пропорции 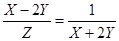 и
и 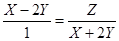 , каждая из которых эквивалентна данному уравнению. Эти пропорции, в свою очередь, эквивалентны соответственно системам уравнений
, каждая из которых эквивалентна данному уравнению. Эти пропорции, в свою очередь, эквивалентны соответственно системам уравнений 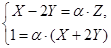 (*) и
(*) и 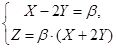 (**), где a и b - любые действительные числа. Так как искомые образующие должны проходить через точку М, то координаты этой точки должны удовлетворять уравнениям этих образующих, т.е.
(**), где a и b - любые действительные числа. Так как искомые образующие должны проходить через точку М, то координаты этой точки должны удовлетворять уравнениям этих образующих, т.е. 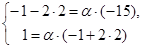 и
и 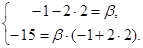 Отсюда a =
Отсюда a = 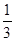 , b =
, b = 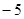 . Подставив (*) и (**), получим
. Подставив (*) и (**), получим
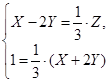 и
и 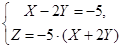 . После преобразований получим общие уравнения двух образующих, проходящих через точку М:
. После преобразований получим общие уравнения двух образующих, проходящих через точку М:
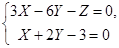 и
и 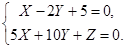
 2015-07-04
2015-07-04 1809
1809






