Частота свободных колебаний называется собственной частотой колебательной системы

Если мячик за одну секунду совершает два колебания, то частота его колебаний составляет 2 Гц. То есть ν = 2Гц.

26. Маятники: физический, математический и пружинный

Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника

Из выражений (142.1) и (140.1) следует, что пружинный маятник совершает гармонические колебания по закону х=А соs (w₀ t + j) с циклической частотой

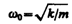(142.2)

и периодом

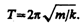(142.3)

Формула (142.3) справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (см. (21.3)), т. е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, согласно (141.5) и (142.2), равна

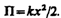
. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 201).

Если маятник отклонен из положения равновесия на некоторый угол a, то в соответствии с уравнением динамики вращательного движения твердого тела (18.3) момент M возвращающей силы можно записать в виде

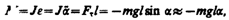
где J — момент инерции маятника относительно оси, проходящей через точку подве­са О, l – расстояние между ней и центром масс маятника, F_t= –mg sina» –mga. — возвращающая сила (знак минус обусловлен тем, что направления F_t и a всегда противоположны; sin a» a соответствует малым колебаниям маятника, т.е. малым отклонениям маятника из положения равновесия). Уравнение (142.4) можно записать в виде

Принимая

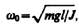(142.5)

получим уравнение

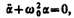
идентичное с (142.1), решение которого (140.1) известно:

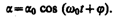(142.6)

Из выражения (142.6) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w₀ (см. (142.5)) и периодом

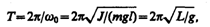(142.7)

где L=J/ (ml) — приведенная длина физического маятника.

Точка О' на продолжении прямой ОС, отстоящая от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 201). Применяя теорему Штейнера (16.1), получим

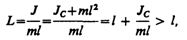
т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса

станет новым центром качаний, и период колебаний физического маятника не изменится.

Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятника

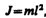(142.8)

где l — длина маятника.

Так как математический маятник можно представить как частный случай физичес­кого маятника, предположив, что вся его масса сосредоточена в одной точке — центре масс, то, подставив выражение (142.8) в формулу (1417), получим выражение для периода малых колебаний математического маятника

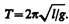(142.9)

Сравнивая формулы (142.7) и (142.9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

25. Сложение гармонических колебаний: колебаний одного направления, взаимно перпендикулярных колебаний