Пусть дана дифференцируемая функция 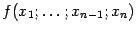 , для которой в некоторой точке
, для которой в некоторой точке 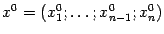 выполнено неравенство
выполнено неравенство
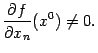
Тогда в некоторой окрестности точки 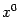 уравнение
уравнение
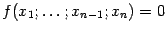
определяет, как мы знаем из теоремы о неявной функции, некоторую функцию 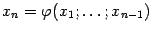 , заданную вблизи точки
, заданную вблизи точки 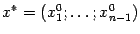 в
в 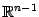 .
.
Пусть требуется найти её частные производные 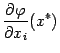 ,
, 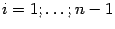 . Это можно сделать, применив формулу производной сложной функции к функции
. Это можно сделать, применив формулу производной сложной функции к функции
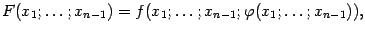
которая тождественно равна 0 в окрестности точки 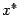 ; следовательно, и все её частные производные в точке
; следовательно, и все её частные производные в точке 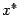 обращаются в 0. Итак, считая параметром, от которого зависят все аргументы функции
обращаются в 0. Итак, считая параметром, от которого зависят все аргументы функции 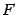 , переменную
, переменную 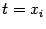 , где
, где 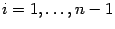 , получаем по формуле
, получаем по формуле 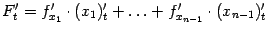 :
:
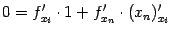
(производные 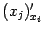 равны 0 при
равны 0 при 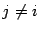 ,
, 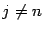 ), то есть
), то есть
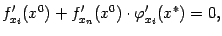
откуда
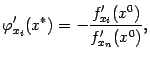
или
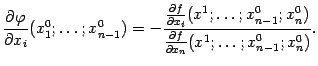
| (7.9) |
Эта важная формула позволяет вычислять производные неявно заданной функции 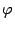 , не имея задающего её явного выражения.
, не имея задающего её явного выражения.
Пример Пусть функция 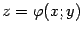 задана неявно уравнением
задана неявно уравнением
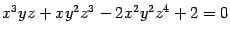
в окрестности точки 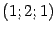 (проверьте, что координаты этой точки удовлетворяют уравнению). Найдём производные
(проверьте, что координаты этой точки удовлетворяют уравнению). Найдём производные 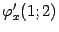 и
и 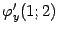 . Поскольку для функции
. Поскольку для функции

частные производные равны
|
|
|
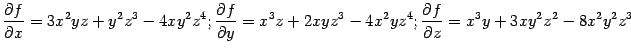
(и 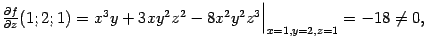
так что данное уравнение действительно определяет неявную функцию), то по формуле (7.9) получаем:
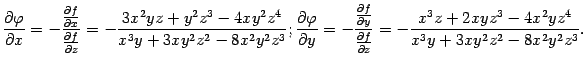
Подставляя координаты точки (1;2;1), находим:
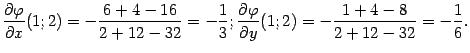
 2015-07-03
2015-07-03 409
409







