Оценка параметров периодических сигналов по экспериментальным данным

Курсовая работа. Часть 1. Задача 1.

Оценка коэффициентов линейной модели методом наименьших квадратов.

% sah548.m

% На пружинные весы поочередно устанавливается груз массой x (г).

% Измеряется сжатие пружины в виде данных вектора y (мм).

x=0:100:800;

y=[0 0.09 0.18 0.28 0.37 0.46 0.55 0.65 0.74];

% Оценить параметры модели y=f(x)=b+a*x методом наименьших квадратов.

% Найти вектор погрешностей измерений. Построить график.

H=[ones(9,1) x'];

d=inv(H'*H)*H'*y'

ym=H*d;

[y' ym]

eps=y'-ym;

plot(x,y,'.',x,ym),grid

Курсовая работа. Часть 1. Задача 2.

Оценка коэффициентов полиномов методом наименьших квадратов.

% Применение функций polyfit и polyval для оценки коэффициентов полиномов.

x1=0:0.1:3;

k=size(x1);

y1=2*x1.^3-0.25*x1.^2+1.2*x1-4;

p1=polyfit(x1,y1,1)

p2=polyfit(x1,y1,2)

p3=polyfit(x1,y1,3)

p4=polyfit(x1,y1,4)

z1=polyval(p1,x1);

z2=polyval(p2,x1);

z3=polyval(p3,x1);

plot(x1,y1,x1,z1,x1,z2,x1,z3,'.'),grid

% Решение этой же задачи с помощью МНК:

H1=[x1.^3;x1.^2;x1;ones(1,k(2))]';

d1=inv(H1'*H1)*H1'*y1'

% Сравнение коэффициентов полинома:

[d1 p3']

Курсовая работа. Часть 1. Задача 3.

Оценка параметров периодических сигналов по экспериментальным данным.

Введение. При малом уровне помех метод наименьших квадратов может эффективно использоваться для разложения периодических функций в ряд Фурье.

Ряды Фурье широко используются в настоящее время для решения важных практических задач. Например, в электроэнергетических системах наиболее эффективно передавать энергию при номинальных значениях частоты и напряжения. Однако в реальных условиях в энергосистемах возникают искажения синусоидальной формы кривых тока и напряжения. Поэтому необходимо отклонения форм кривых тока и напряжения от правильной синусоидальной формы оценивать по гармоническим составляющим периодических сигналов.

Постановка задачи.

В процессе обработки периодического сигнала получены значения силы тока через каждые s4 ° в контрольных точках в интервале изменения угла alf= 0° 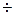360°. Полученные значения удовлетворяют равенствам:

при alf= 0° 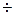180° i4= alf/18 Ампер,

при alf= 18 0° 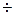360° i4= 10-1/(alf-180)*18 Ампер.

Требуется по экспериментальным данным определить амплитуды и фазы первых пяти гармоник периодического сигнала силы тока.

Математическая модель задачи.

Периодический сигнал имеет вид (1):

I(w₀t)=I_1m*sin(w₀t+F1)+ I_2m*sin(2*w₀t+F2)+ I_3m*sin(3*w₀t+F3)+ I_4m*sin(4*w₀t+F4)+ I_5m*sin(5*w₀t+F5)+…

где w₀ - частота первой гармоники. Таким образом, требуется оценить амплитуды I₁_m, I₂_m_, I₃_m, I₄_m, I₅_m и фазы F1, F2, F3, F4, F5.

Введем обозначения (2)

x(1)= I_1m*cosF1;

x(2)= I_1m*sinF1;

x(3)= I_2m*cosF2;

x(4)= I_2m*sinF2;

x(5)= I_3m*cosF3;

x(6)= I_3m*sinF3;

x(7)= I_4m*cosF4;

x(8)= I_4m*sinF4;

x(9)= I_5m*cosF5;

x(10)= I₅_m*sinF5.

Эти величины в уравнении (1) являются постоянными. I(w₀t) является скалярной величиной. Она может быть получена в виде произведения двух векторов: вектор-строки [sinw₀ t cos w₀ t sin 2w₀ t cos 2w₀ t sin 3w₀ t cos 3w₀ t] и вектор-столбца х, образованного из элементов

x = [x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10)]^T, т.е

I(w₀t)=[sinw₀ t cos w₀ t sin 2w₀ t cos 2w₀ t sin 3w₀ t cos 3w₀ t]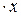

Вектор x является искомым вектором, содержащим десять неизвестных коэффициентов.

C помощью вектор-строки приведенного выше уравнения сформируем матрицу H размерности (1441х11), где каждая i -ая строка должна содержать значения элементов, соответствующие углу alf(i), приведенному в i - ой ячейке первой строки таблицы. B среде MatLAB эта операция выполняется с помощью m-файла.