Рассмотрим гамильтонову систему с двумя степенями свободы: частица движется на плоскости и ее положение определяется вектором 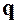 . Пусть гамильтониан явно не зависит от времени и поэтому энергия сохраняется:
. Пусть гамильтониан явно не зависит от времени и поэтому энергия сохраняется:
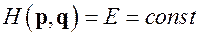 . (15)
. (15)
Фазовое пространство четырехмерно. Фазовые траектории находятся на трехмерной энергетической гиперповерхности. Соотношение (15) позволяет, по крайней мере, локально выразить любую из четырех переменных как функцию трех остальных, например
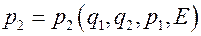 . (16)
. (16)
Таким образом, фазовое пространство фактически становится трехмерным 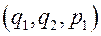 (если нет дополнительных интегралов движения). Выберем в этом трехмерном пространстве некоторую поверхность
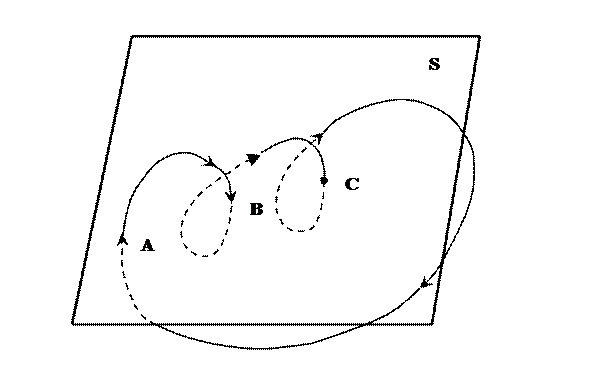
(если нет дополнительных интегралов движения). Выберем в этом трехмерном пространстве некоторую поверхность 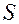 , например, некоторую плоскость и рассмотрим ее последовательные пересечения фазовой траекторией в направлении возрастания времени.
, например, некоторую плоскость и рассмотрим ее последовательные пересечения фазовой траекторией в направлении возрастания времени.
При этом получим некоторую последовательность точек пересечения
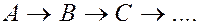
Такое отображение точек на поверхности 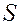 осуществляется с помощью некоторой функции
осуществляется с помощью некоторой функции 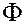 :
:
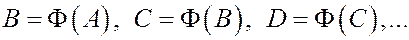
Опр. Функция 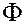 наз. функцией последования или отображением
наз. функцией последования или отображением
|
|
|
Пуанкаре.
Совокупность точек 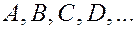 также называется отображением Пуанкаре.
также называется отображением Пуанкаре.
Понятие отображения Пуанкаре можно распространить и на системы с
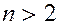 . Для автономных систем размерность энергетической гиперповерхности, на которой расположены фазовые кривые, равна
. Для автономных систем размерность энергетической гиперповерхности, на которой расположены фазовые кривые, равна
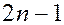 . В этом случае рассматриваются последовательные точки пересечения траектории динамической системы с
. В этом случае рассматриваются последовательные точки пересечения траектории динамической системы с 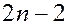 - мерной гиперповерхностью
- мерной гиперповерхностью 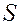 при условии, что поток нигде не касается
при условии, что поток нигде не касается 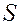 , а «протыкает» ее. Если помимо интеграла энергии имеется еще
, а «протыкает» ее. Если помимо интеграла энергии имеется еще 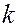 интегралов движения, то размерность усеченного фазового пространства равна
интегралов движения, то размерность усеченного фазового пространства равна 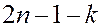 , а размерность гиперповерхности равна
, а размерность гиперповерхности равна 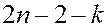 .
.
Если известна структура следов на секущей поверхности 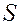 , это дает возможность наглядно представить динамику системы.
, это дает возможность наглядно представить динамику системы.
Так называемому квазипериодическому движению соответствует отображение Пуанкаре, множество точек которого плотно заполняет определенную замкнутую кривую.

Наконец существуют системы, для которых при некоторых условиях траектория на 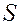 представлена хаотическим множеством точек. Режим эволюции таких точек не является ни периодическим, ни квазипериодическим.
представлена хаотическим множеством точек. Режим эволюции таких точек не является ни периодическим, ни квазипериодическим. 
Раздел. Интегрируемые системы.
Мы уже говорили - уравнения Гамильтона обладают тем важным свойством, что допускают широкий класс преобразований канонических переменных 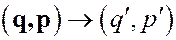 (канонические преобразования), при которых не изменяется общая форма уравнений для любой гамильтоновой системы:
(канонические преобразования), при которых не изменяется общая форма уравнений для любой гамильтоновой системы:
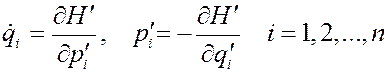 (1)
(1)
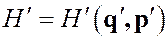 , (2)
, (2)
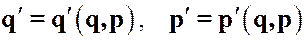 . (3)
. (3)
Такие преобразования могут быть полезны при построении решений и анализе физической картины движения.
Одно из важных и часто используемых преобразований является преобразование
|
|
|
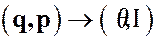 , (4)
, (4)
при котором в новых переменных 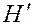 не зависит от координат
не зависит от координат 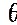 :
:
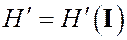 . (5)
. (5)
В этом случае переменные 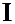 называются переменными действия, а соответствующие сопряженные переменные
называются переменными действия, а соответствующие сопряженные переменные 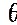 называются переменными типа угол.
называются переменными типа угол.
Такие преобразования однако возможны лишь в определенных специальных случаях.
В этих случаях имеем
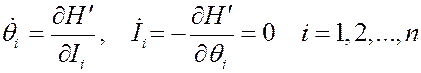 . (6)
. (6)
Эта система легко интегрируется:
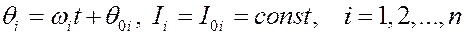 . (7)
. (7)
Отсюда по формулам преобразований можно найти исходные координаты и импульсы:
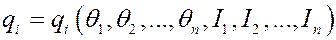 , (8)
, (8)
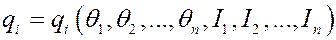 . (9)
. (9)
Опр. Гамильтонова система (1) наз. полностью интегрируемой, если существует каноническое преобразование, с помощью которого можно перейти к переменным действие-угол.
 2015-07-04
2015-07-04 1280
1280








