2015-07-04
352
Тесты - выпуклое программирование
1*. Множество точек называется выпуклым, если
1 – оно является многоугольником;
2 – оно вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки;
3 – большинство точек отрезка принадлежит данному множеству;
4 – отрезок, соединяющий любые две несовпадающие точки множества, целиком принадлежит этому множеству.
2. Функция называется выпуклой, если
1 – она является строго вогнутой;
2 – она определена на выпуклом множестве W;
3 – она определена на выпуклом множестве W и выполняется условие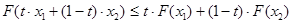 
для любых точек х1,х2 Î W и для любого t Î [0,1];
4 - она определена на выпуклом множестве W и выполняется условие F(αX1 + (1-α/2)X2) ≤ αF(X1) + (1-α/2)F(X2) для любых точек х1,х2 Î W и для любого t Î [0,1].
3. Функция называется гладкой, если
1 – непрерывны ее первые производные;
2 – непрерывны ее первая и вторая производные;
3 – на переменные наложено условие неотрицательности.
4. Какая функция имеет локальный максимум?
1 – если в окрестностях точки Х* выполняется неравенство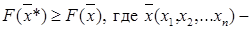 
любая точка, принадлежащая окрестности любого, в том числе бесконечно малого радиуса;
|
|
|
2 – если в окрестностях точки Х* выполняется неравенство 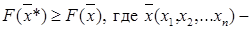любая точка, принадлежащая области определения функции;
3 – если в окрестностях точки Х* выполняется неравенство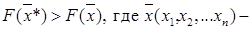 
любая точка, принадлежащая окрестности любого, в том числе бесконечно малого радиуса.
5. Какая функция имеет абсолютный максимум?
1 – если в окрестностях точки Х* выполняется неравенство 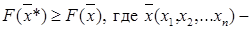любая точка, принадлежащая окрестности бесконечно малого радиуса;
2 – если в окрестностях точки Х* выполняется неравенство 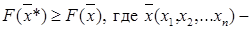любая точка, принадлежащая области определения функции;
3 – если в окрестностях точки Х* выполняется неравенство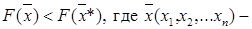 
любая точка, принадлежащая определенному множеству.
6. Задача называется выпуклой, если она имеет
1 – выпуклую целевую функцию;
2 – выпуклую систему ограничений и выпуклую целевую функцию;
3 – выпуклую целевую функцию и нелинейную систему ограничений;
7. «Если область D замкнута и ограничена, то дифференцируемая функция
z = f(x) достигает в этой области своего наибольшего или наименьшего значений или в стационарной точке, или в граничной точке области».
1 – теорема Ляпунова;
2 – теорема Неймана;
3 – теорема Вейерштрасса;
4 – теорема Лагранжа.
8*. Градиентные методы:
1 – наискорейшего подъема;
2 – штрафных функций;
3 –наискорейшего спуска;
4 – локального случайного поиска;
5 – нелокального случайного поиска.
9. В чем отличие метода локального случайного поиска от метода нелокального случайного поиска?
1 – в формировании случайного вектора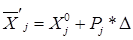 
;
|
|
|
2 – в формировании случайного вектора
;
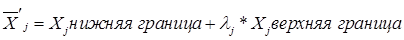3 – в ограничении количества проводимых испытаний;
4 – в задании начального вектора Х0.
10*. В чем отличие метода штрафных функций при решении задачи выпуклого программирования и задачи линейного программирования?
1 – определяется число М для задания функции штрафов, формируется массив случайных чисел, находится функция штрафов, определяется конечное число неудачных испытаний;
2 – задаются числа Мj для задания функции штрафов для каждого ограничения, формируется массив случайных чисел, находится функция штрафов, определяется конечное число неудачных испытаний;
3 – для задачи линейного программирования штрафные функции подбираются так, чтобы избежать узких гребней, затрудняющих применение методов поиска безусловных экстремумов;
4 – параметр М в процессе решения задачи меняется от малой величины до большой.
11. Все методы решения, основанные на исследовании функций в небольшой окрестности последовательно выбираемых точек, называют
1 – методами отсечения;
2 – методами поиска;
3 – методами возможных направлений;
12. Градиентом функции называется
1 – вектор, проекциями которого на координатные оси служат соответствующие частные производные, т.е. Ñ F =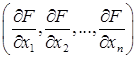 
;
2 – вектор, направление которого указывает скорость убывания функции в этой точке;
3 – отрезок, ограничивающий область определения функции.
13. Функция называется сепарабельной, если
1 – ее можно представить в виде суммы функций, каждая из которых зависит только от одной переменной;
2 – ее можно представить в виде квадратичной функции;
3 – она содержит константу.
14*. Приближенное решение задач выпуклого программирования градиентным методом заключается
1 – в задании «выгодного» направления приближения к оптимальному решению;
2 – в нахождении оптимального решения за наименьшее число шагов;
3 – в поиске точки начального приближения;
4 – в нахождении приближенного значения оптимального решения в определенной области решения.
15*. Градиентный метод называется «методом наискорейшего спуска», если
1 – величина длины шага выбирается так, что приращение функции при перемещении из точки Х0 в точку Х1 будет наибольшим при решении задачи на минимум;
2 – величина длины шага выбирается так, что приращение функции при перемещении из точки Х0 в точку Х1 будет наименьшим при решении задачи на минимум;
3 – величина длины шага выбирается так, что приращение функции при перемещении из точки Х0 в точку Х1 будет наименьшим при решении задачи на минимум и наибольшим при решении задачи на максимум.
16. Для задач выпуклого программирования справедлива теорема: необходимым и достаточным условием оптимальности вектора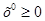 
является существование вектора 
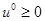такого, что пара 
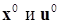будет седловой для соответствующей функции Лагранжа, т.е. 
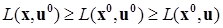при всех , .
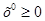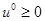1 – теорема двойственности;
2 – теорема Лагранжа;
3 – теорема Куна–Таккера;
4 – теорема Эйлера.
Тесты - квадратичное программирование
1. Какая задача называется задачей квадратичного программирования?
1 – задача, имеющая квадратичную целевую функцию (целевая функция содержит переменные во второй степени) и систему ограничений – квадратичные выражения;
2 – задача, имеющая квадратичную целевую функцию (целевая функция содержит переменные во второй степени), а система ограничений - линейные выражения;
3 – задача, имеющая квадратичную целевую функцию (целевая функция содержит переменные во второй степени), а система ограничений - нелинейные выражения.
2. Какие задачи квадратичного программирования удобнее всего решать графическим методом?
1 – имеющие n переменных;
2 – имеющие 3 переменные;
3 – имеющие 2 переменные.
|
|
|
3. Что представляет область допустимых решений (ОДР) задач квадратичного программирования?
1 – выпуклый многоугольник, либо выпуклая неограниченная область с конечным числом вершин;
2 – только выпуклый многоугольник;
3 – только выпуклая неограниченная область с конечным числом вершин.
4*. Что представляет линия уровня целевой квадратичной функции?
1 – прямую;
2 – кривую n порядка;
3 – кривую 3 порядка;
4 – кривую 2 порядка.
5. Какие перечисленные кривые относятся к целевой квадратичной функции?
1 – концентрические окружности;
2 – подобные эллипсы;
3 – подобные параболы;
4 – окружность, эллипс, гипербола, парабола.
6. Если в задаче квадратичного программирования Z(X1,X2) = =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11=C22>0, то к какому виду приводим целевую функцию?
1 – Z(X1,X2)= C11(X1 -a)2 -C22 (X2-b)2+C0;
2 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2+C0;
3 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2.
7. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11=C22<0, то к какому виду приводим целевую функцию?
1 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2+C0;
2 – Z(X1,X2)= C11(X1 -a)2 -C22 (X2-b)2+C0;
3 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2.
8. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22 и оба положительные; C11·C22>0, то к какому виду приводим целевую функцию?
1 – Z(X1,X2)= C11(X1 -a)2 -C22 (X2-b)2+C0;
2 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2;
3 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2 +C0.
9. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22 и оба отрицательные; C11·C22 >0, то к какому виду приводим целевую функцию?
1 – Z(X1,X2)= C11(X1 -a)2 -C22 (X2-b)2;
2 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2+C0;
3 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2.
10. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22, а C11·C22 <0, то к какому виду приводим целевую функцию?
1 – Z(X1,X2)= C11(X1 -a)2 -C22 (X2-b)2+C0;
2 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2+C0;
3 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2.
11. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
|
|
|
C22 =0, C2 не равно нулю, то к какому виду приводим целевую функцию?
1 – Z(X1,X2)= C11(X1 -a)2 -C22 (X2-b)2+C0;
2 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2+C0;
3 – Z(X1,X2)= aX1 2 +bX1+c - X2.
12. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C 11 =0, C1 не равно нулю, то к какому виду приводим целевую функцию?
1 – Z(X1,X2)= aX2 2 +bX1+c - X1;
2 – Z(X1,X2)= C11(X1 -a)2 -C22 (X2-b)2+C0;
3 – Z(X1,X2)= C11(X1 -a)2 +C22 (X2-b)2+C0.
13. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C2= C22 =0, то к какому виду приводим целевую функцию Z(X1,X2)= C11X12 +C1X1+C0 ?
1 – Z(X1,X2)= aX2 2 +bX1+c - X1;
2 – Z(X1,X2)= aX1 2 +bX1+c;
3 – Z(X1,X2)= aX2 2 +bX2+c.
14. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C1=C11=0,то к какому виду приводим целевую функцию Z(X1,X2)= C22X22 +C2X2 +C0 ?
1 – Z(X1,X2)= aX2 2 +bX1+c - X1;
2 – Z(X1,X2)= aX1 2 +bX1+c;
3 – Z(X1,X2)= aX2 2 +bX2+c.
15. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11=C22>0, то в какой точке находится центр или вершина целевой функции?
1 – O`(a,b);
2 – O`(C11,C22);
3 – O`(-C11,-C22).
16. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11=C22<0, то в какой точке находится центр или вершина целевой функции?
1 – O`(C11,C22);
2 – O`(a,b);
3 – O`(-C11,-C22).
17. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22 и оба положительные; C11·C22>0, то в какой точке находится центр или вершина целевой функции?
1 – O`(C11,C22);
2 – O`(-C11,-C22);
3 – O`(a,b).
18. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22 и оба отрицательные; C11·C22 >0, то в какой точке находится центр или вершина целевой функции?
1 – O`(C11,C22);
2 – O`(a,b);
3 – O`(-C11,-C22).
19. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22, а C11·C22 <0, то в какой точке находится центр или вершина целевой функции?
1 – O`(a,b);
2 – O`(C11,C22);.
3 – O`(-C11,-C22).
20. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C22 =0, C2 не равно нулю, то в какой точке находится центр или вершина целевой функции?
1 – (-b/2a; X2);
2 – (X1;-b/2a);
3 – (a,b).
21. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C 11 =0, C1 не равно нулю, то в какой точке находится центр или вершина целевой функции?
1 – (-b/2a; X2);
2 – (X1;-b/2a);
3 – (a,b).
22. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C2= C22 =0, то как изображается целевая функция
Z(X1,X2)= C11X12 +C1X1+C0 ?
1 – подобные параболы, ось симметрии которых параллельна оси ОX2, а вершина имеет координаты (-b/2a; X2);
2 – подобные параболы, ось симметрии которых параллельна оси ОX1, а вершина имеет координаты (X1;-b/2a);
3 – прямые, параллельные оси ОX2, если b2-4ac >0 и мнимое место точек, если b2-4ac <0;
4 – прямые, параллельные оси ОX1, если b2-4ac >0 и мнимое место точек, если b2-4ac <0.
23. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C1=C11=0, то как изображается целевая функция
Z(X1,X2)= C11X12 +C1X1+C0 ?
1 – подобные параболы, ось симметрии которых параллельна оси ОX2, а вершина имеет координаты (-b/2a; X2);
2 – подобные параболы, ось симметрии которых параллельна оси ОX1, а вершина имеет координаты (X1;-b/2a);
3 – прямые, параллельные оси ОX2, если b2-4ac >0 и мнимое место точек, если b2-4ac <0;
4 – прямые, параллельные оси ОX1, если b2-4ac >0 и мнимое место точек, если b2-4ac <0.
24. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C22 =0, C2 не равно нулю, то как изображается целевая функция Z(X1,X2)= =C22X12 +C2X2+C0 ?
1 – подобные параболы, ось симметрии которых параллельна оси ОX2, а вершина имеет координаты (–b/2a; X2);
2 – подобные параболы, ось симметрии которых параллельна оси ОX1, а вершина имеет координаты (X1;–b/2a);
3 – прямые, параллельные оси ОX2, если b2–4ac >0 и мнимое место точек, если b2–4ac <0;
4 – прямые, параллельные оси ОX1, если b2-4ac >0 и мнимое место точек, если b2–4ac <0.
25. Если в задаче квадратичного программирования Z(X1,X2) = =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C22 =0, C2 не равно нулю, то как изображается целевая функция Z(X1,X2)= =aX1 2 +bX1+c - X2?
1 – подобные параболы, ось симметрии которых параллельна оси ОX2, а вершина имеет координаты (-b/2a; X2);
2 – подобные параболы, ось симметрии которых параллельна оси ОX1, а вершина имеет координаты (X1;-b/2a);
3 – прямые, параллельные оси ОX2, если b2-4ac >0 и мнимое место точек, если b2-4ac <0;
4 – прямые, параллельные оси ОX1, если b2-4ac >0 и мнимое место точек, если b2-4ac <0.
26. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11·C22 =0, причём одновременно C11 и C22 равняться нулю не могут:
C 11 =0, C1 не равно нулю, то как изображается целевая функция Z(X1,X2)= aX2 2 +bX2+c - X1.
1 – подобные параболы, ось симметрии которых параллельна оси ОX2, а вершина имеет координаты (-b/2a; X2);
2 – подобные параболы, ось симметрии которых параллельна оси ОX1, а вершина имеет координаты (X1;-b/2a);
3 – прямые, параллельные оси ОX2, если b2-4ac >0 и мнимое место точек, если b2-4ac <0;
4 – прямые, параллельные оси ОX1, если b2-4ac >0 и мнимое место точек, если b2-4ac <0.
27. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11=C22>0, то к какой из перечисленных кривых относится целевая квадратичная функция?
1 – концентрические окружности;
2 – подобные эллипсы;
3 – подобные гиперболы;
4 – подобные параболы;
5 – концентрические мнимые окружности;
6 – подобные мнимые эллипсы.
28. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11=C22<0, то к какой из перечисленных кривых относится целевая квадратичная функция?
1 – концентрические окружности;
2 – подобные эллипсы;
3 – подобные гиперболы;
4 – подобные параболы;
5 – концентрические мнимые окружности;
6 – подобные мнимые эллипсы.
29. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22 и оба положительные; C11·C22>0, то к какой из перечисленных кривых относится целевая квадратичная функция?
1 – концентрические окружности;
2 – подобные эллипсы;
3 – подобные гиперболы;
4 – подобные параболы;
5 – концентрические мнимые окружности;
6 – подобные мнимые эллипсы;
30. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22 и оба отрицательные; C11·C22 >0, то к какой из перечисленных кривых относится целевая квадратичная функция?
1 – концентрические окружности;
2 – подобные эллипсы;
3 – подобные гиперболы;
4 – подобные параболы;
5 – концентрические мнимые окружности;
6 – подобные мнимые эллипсы.
31. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22, а C11·C22 <0, то к какой из перечисленных кривых относится целевая квадратичная функция?
1 –концентрические окружности;
2 – подобные эллипсы;
3 – подобные гиперболы;
4 – подобные параболы;
5 – концентрические мнимые окружности;
6 – подобные мнимые эллипсы.
32. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22 и оба положительные; C11·C22>0, то чему равно отношение полуосей целевой квадратичной функции?
1 – корню квадратному из отношения C22 к C11;
2 – корню квадратному из отношения C11 к C22;
3 – корню квадратному из модуля отношения C22 к C11;
4 – корню квадратному из модуля отношения C11 к C22 .
33. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22 и оба отрицательные; C11·C22 >0, то чему равно отношение полуосей целевой квадратичной функции?
1 – корню квадратному из модуля отношения C22 к C11;
2 – корню квадратному из отношения C11 к C22;
3 – корню квадратному из отношения C22 к C11;
4 – корню квадратному из модуля отношения C11 к C22 .
34. Если в задаче квадратичного программирования Z(X1,X2)= =C11X12+C22X22+C1X1+C2X2 +C0
aI1 X1 +aI2X2.≤aI 0 , i=1÷m,
X1≥0, X2≥0,
C11 не равно C22, а C11·C22 <0, то какой вид имеют уравнения асимптот?
1 – X2 = b + K (X1 -a) и X2 =b -K (X1 -a). Коэффициент K равен корню квадратному из отношения C11 к C22;
2 – X2 = b + K (X1 -a) и X2 =b -K (X1 -a). Коэффициент K равен корню квадратному из модуля отношения C11 к C22;
3 – X1 = b + K (X2 -a) и X1 =b -K (X2 -a). Коэффициент K равен корню квадратному из модуля отношения C11 к C22;
4 – X1= b + K (X2 -a) и X1 =b -K (X2 -a). Коэффициент K равен корню квадратному из отношения C11 к C22.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Основная литература
1. Абрамов Л.М., Капустин В.Ф. Математическое программирование. Л.: Изд-во ЛГУ, 1981.
2. Красс М.С. Математические методы и модели. М.: Финансы и статистика, 2007.
3. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. М.: ДЕЛО, 2001.
4. Красс М.С., Чупрынов Б.П. Основы математики. М.: Финансы и статистика, 2005.
5. Кремер Н.Ш. и др. Высшая математика для экономистов. М.: ЮНИТИ, 1998
6. Кремер Н.Ш. и др. Исследование операций в экономике. М.: ЮНИТИ, 1997, 2003, 2004.
7. Кузнецов Б.Т. Математические методы и модели исследования операций: Профессиональный учебник. М.: ЮНИТИ, 2005.
8. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М.: Высшая школа, 1980, 1986.
9. Лядина Н.Г., Ермакова Е.А., Светлова Г.Н., Уразбахтина Л.В. Математические методы в экономике АПК. Нелинейное программирование и модели исследования операций: Практикум. М.: Изд-во РГАУ – МСХА имени К.А. Тимирязева, 2011.
10. Лядина Н.Г., Ермакова Е.А., Светлова Г.Н., Уразбахтина Л.В., Хотов А.В. Практикум. Математические методы в экономике АПК. (Линейное и дискретное программирование). М.: Изд-во РГАУ – МСХА имени К.А. Тимирязева, 2009.
11. Математические методы в экономике: Учеб. Пособие / Л.Э. Хазанова. 3-е изд., стереотип. М., Волтерс Клувер, 2005.
12. Математическое программирование / Под ред. Н.Ш. Кремера. М.: Финстатинформ, 1995.
13. Невежин В.П., Кружилов С.И. Сборник задач по курсу «Экономико-математическое моделирование». –М.: ОАО «Издательский дом «Городец»», 2005. – 320 с.
14. Просветов Г.И. Математические методы и модели в экономике: задачи и решения: Учебно-практическое пособие. – М., Издательство «Альфа-Пресс», 2008.
15. Шапкин А.С., Мазаева Н.П. Математические методы и модели исследования операций: Учебник. М.: Дашков и К°, 2005.
16. Экономико-математические методы и прикладные модели: Уч. пособие для вузов. Под ред. В.В.Федосеева.-2-е изд., перераб. и доп. – М.:ЮНИТИ-ДАНА, 2005.
Дополнительная литература
1. Акулич И.Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1986.
2. Волков Е.А. Численные методы. М.: Наука, 1982.
3. Гусева Е.Н. Экономико-математическое моделирование: учебное пособие / Е.Н. Гусева. –М.: Флинта: МПСИ, 2008.
4. Кофман А., Фор Р. Займемся исследованием операций. М.: Мир, 1966.
5. Лядина Н.Г., Лядин В.П., Уразбахтина Л.В. Классификация задач линейного и нелинейного программирования. Эквивалентные формы записи задач линейного программирования. М.: ФГОУ ВПО РГАУ - МСХА, 2007.
6. Лядина Н.Г., Плетцова И.И. Выпуклое программирование. М.: МСХА, 1989.
7. Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983.
8. Пшеничный Б.Н. Необходимые условия экстремума. М.: Наука, 1982.
9. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Ч. 1. М.: Финансы и статистика, 2001, 2007.
