Следствие это мы доказали выше, как теорема каратеодори для конусов.

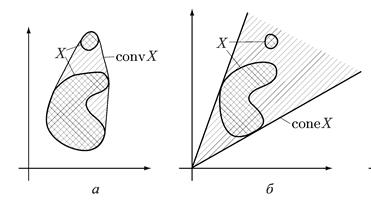

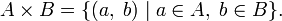 декартовопроизведение, дальше понадобится.
декартовопроизведение, дальше понадобится.
Теоремы об отделимости.
Пусть 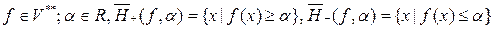
По определению Х и У отделимы, если 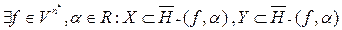 \\\Другими словами, можно разделить чем-то два множества.
\\\Другими словами, можно разделить чем-то два множества.

Сильная и строгая отделимость – одно и то же.
Просто теорема
Х и У – строго отделимы(отделимы), т.и.т.т. Z=X-Y и {0} строгоотделимы(отделимы)
Первая теорема об отделимости.
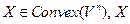 -замкнуто,
-замкнуто, 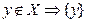 и Х – строго отделимы.
и Х – строго отделимы.
Вторая теорема об отделимости(строгой).
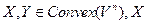 -компакт, У – замкнутое множество и пересечение этих множеств пустое.
-компакт, У – замкнутое множество и пересечение этих множеств пустое.
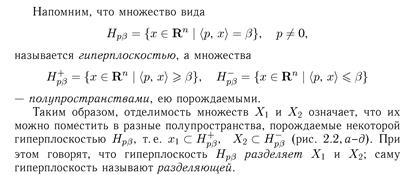 Условие компактности убрать нельзя. Контрпример:
Условие компактности убрать нельзя. Контрпример:
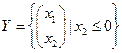
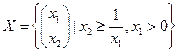
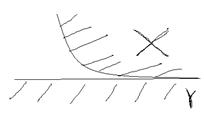
Разделяющая функция 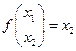 , но нет строгой отделимости.
, но нет строгой отделимости.
Третья теорема об отделимости.
Если  и пересечение этих множеств пустое, то Х и У отделимы. \\\Опорные гиперплоскости
и пересечение этих множеств пустое, то Х и У отделимы. \\\Опорные гиперплоскости
Пусть Х – выпуклое множество, 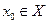 . Пусть f-функционал, разделяющий Х и {x0}. Обозначим полупространство, состоящее из всех точек, где выполняется неравенство
. Пусть f-функционал, разделяющий Х и {x0}. Обозначим полупространство, состоящее из всех точек, где выполняется неравенство 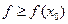 через
через 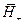 . Тогда
. Тогда 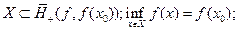 Тогда f называется опорный(разделяющий) функционал, а
Тогда f называется опорный(разделяющий) функционал, а 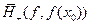 - опорное полупространство в т. х0 к Х. Н – опорная гиперплоскость к Х.
- опорное полупространство в т. х0 к Х. Н – опорная гиперплоскость к Х. 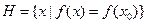
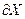 - множество граничных точек.
- множество граничных точек.
 Теорема(без доказательства)
Теорема(без доказательства)
 Если
Если 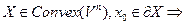 существует опорная гиперплоскость к Х в т. х0.
существует опорная гиперплоскость к Х в т. х0.
 Экстремальные точки.
Экстремальные точки.


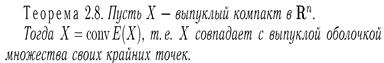 Теорема Минковского.
Теорема Минковского.
Лемма(без док.): 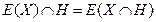
Доказательство теоремы Минковского.
 Проведем индукции по dim(X). Если dim(X) = 0, то теорема очевидна. Пусть теорема доказана для размерности m-1 и пусть dim(X)=m.
Проведем индукции по dim(X). Если dim(X) = 0, то теорема очевидна. Пусть теорема доказана для размерности m-1 и пусть dim(X)=m.
1. 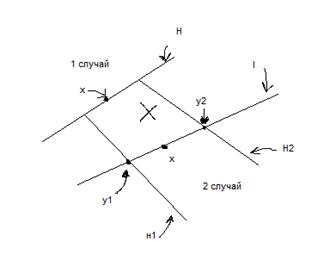 Пусть
Пусть 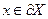 (граничная точка). Н-опорная гиперплоскость к Х в т х:
(граничная точка). Н-опорная гиперплоскость к Х в т х: 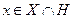 . Тогда по предположению индукции
. Тогда по предположению индукции 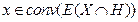 , т.к.
, т.к. 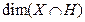 <m; По лемме, указанной выше получаем, что
<m; По лемме, указанной выше получаем, что 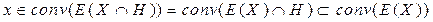 Т.к.
Т.к. 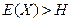 , то вып. Оболочка Н содержится в Е(Х).
, то вып. Оболочка Н содержится в Е(Х).
2. 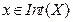 -(внутренность Х). Т.к. Х – компакт, то прямая l проведенная через т х будет на Х отрезком.
-(внутренность Х). Т.к. Х – компакт, то прямая l проведенная через т х будет на Х отрезком. 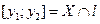 , тогда
, тогда 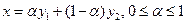 . С другой стороны у1 и у2
. С другой стороны у1 и у2 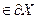 , следовательно, мы можем построить 2 опорные гиперплоскости к Х через т у1 и у2: Н1 и Н2 – опорные гиперплоскости соответственно.
, следовательно, мы можем построить 2 опорные гиперплоскости к Х через т у1 и у2: Н1 и Н2 – опорные гиперплоскости соответственно. 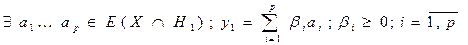
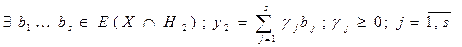 откуда получаем, что
откуда получаем, что 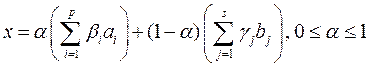 , т.к. т х лежит на отрезке, с концами в т. у1 и у2. Сопряженные конусы. Пусть
, т.к. т х лежит на отрезке, с концами в т. у1 и у2. Сопряженные конусы. Пусть 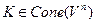 . К* =
. К* = 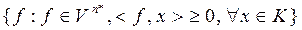
Их свойства. 1) 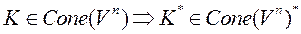 2)
2) 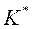 -замкнут при любом
-замкнут при любом 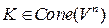
3) 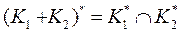 4)
4) 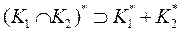 \\\\ Лемма Фаркаша(абстрактная форма)\\\ Пусть К – замкнутый конус, К=К** Доказательство.
\\\\ Лемма Фаркаша(абстрактная форма)\\\ Пусть К – замкнутый конус, К=К** Доказательство.
Пусть
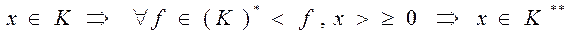 т.к.
т.к.
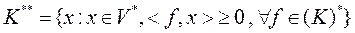
Пусть 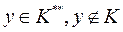 тогда по первой теоремы об отделимости
тогда по первой теоремы об отделимости 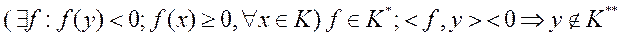 противоречие.
противоречие.
2) Выпуклые функции, их свойства, Определение. 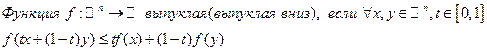
 (в общем случае функция определена на выпуклом подмножестве некоторого векторного пространства)\\\Если неравенство строгое для любого
(в общем случае функция определена на выпуклом подмножестве некоторого векторного пространства)\\\Если неравенство строгое для любого 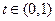 - функция называется строго выпуклой. Если выполняется обратное неравенство, функция называется вогнутой, или выпуклой вверх (если неравенство строгое - строго вогнутой).\\\Если
- функция называется строго выпуклой. Если выполняется обратное неравенство, функция называется вогнутой, или выпуклой вверх (если неравенство строгое - строго вогнутой).\\\Если  - выпуклое множество, то
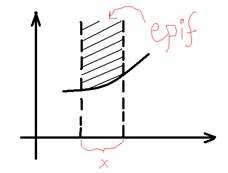
- выпуклое множество, то 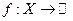 -выпуклая функция.\\\Определение. Надграфик
-выпуклая функция.\\\Определение. Надграфик 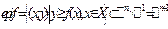 \\Теорема.
\\Теорема. 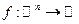 \\\ 1) если f – выпуклая функция, то
\\\ 1) если f – выпуклая функция, то 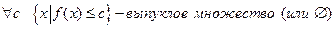 \\\2) функция f выпуклая
\\\2) функция f выпуклая  epif – выпуклое подмножество в
epif – выпуклое подмножество в  .\\\\ Доказательство: \\\ 1)очевидно.2)(
.\\\\ Доказательство: \\\ 1)очевидно.2)( ) f-выпуклая функция. Взяли точки А и В в надграфике, нужно доказать, что отрезок, соединяющий эти точки, также принадлежит этому надграфику.
) f-выпуклая функция. Взяли точки А и В в надграфике, нужно доказать, что отрезок, соединяющий эти точки, также принадлежит этому надграфику.
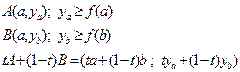 \\\\Точка принадлежит надграфику, если\\\
\\\\Точка принадлежит надграфику, если\\\ 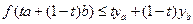 , но так как функция f выпуклая, выполняется
, но так как функция f выпуклая, выполняется 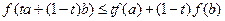 , но, так как
, но, так как 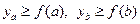 , то верно и
, то верно и 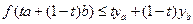
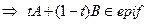 \\\\Так как точки А и В любые, надграфик – выпуклое множество.\\\
\\\\Так как точки А и В любые, надграфик – выпуклое множество.\\\ 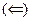 Надграфик - выпуклое множество\\\\ Вновь берем точки А и В в надграфике, в нем лежит и отрезок, соединяющий их. \\\\
Надграфик - выпуклое множество\\\\ Вновь берем точки А и В в надграфике, в нем лежит и отрезок, соединяющий их. \\\\ 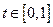 :
: 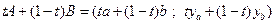 \\\\Выполняется
\\\\Выполняется 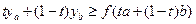 \\\С другой стороны,
\\\С другой стороны, 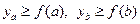 , следовательно
, следовательно 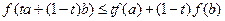 , то есть f – выпуклая функция, ч.т.д.\\\ Свойства выпуклой функции.1) Функция f, выпуклая на интервале C, непрерывна на всём C и дифференцируема на всём C за исключением не более чем счётного множества точек.Но в точках, в которых функция не дифференцируема, есть правая и левая производные.\\\\Например:
, то есть f – выпуклая функция, ч.т.д.\\\ Свойства выпуклой функции.1) Функция f, выпуклая на интервале C, непрерывна на всём C и дифференцируема на всём C за исключением не более чем счётного множества точек.Но в точках, в которых функция не дифференцируема, есть правая и левая производные.\\\\Например:  \\\) 2) Непрерывно дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её график лежит не ниже касательной, проведённой к этому графику в любой точке промежутка выпуклости. \\\3) Дважды дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её вторая производная неотрицательна на этом интервале. Если вторая производная дважды дифференцируемой функции строго положительна, такая функция является строго выпуклой, однако обратное неверно (например, функция f (x)= x 4 строго выпукла на [-1,1], но её вторая производная в точке x =0 равна нулю).\\\ 4) Если функции f, g выпуклы, то любая их линейная комбинация a f + b g с положительными коэффициентами a, b также выпукла.\\\ 5) Локальный минимум выпуклой функции является также глобальным минимумом (соответственно, для выпуклых вверх функций локальный максимум является глобальным максимумом).\\\ 6) Любая стационарная точка выпуклой функции будет глобальным экстремумом.\\\ 7) Для выпуклых функций выполняется неравенство Йенсена:
\\\) 2) Непрерывно дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её график лежит не ниже касательной, проведённой к этому графику в любой точке промежутка выпуклости. \\\3) Дважды дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её вторая производная неотрицательна на этом интервале. Если вторая производная дважды дифференцируемой функции строго положительна, такая функция является строго выпуклой, однако обратное неверно (например, функция f (x)= x 4 строго выпукла на [-1,1], но её вторая производная в точке x =0 равна нулю).\\\ 4) Если функции f, g выпуклы, то любая их линейная комбинация a f + b g с положительными коэффициентами a, b также выпукла.\\\ 5) Локальный минимум выпуклой функции является также глобальным минимумом (соответственно, для выпуклых вверх функций локальный максимум является глобальным максимумом).\\\ 6) Любая стационарная точка выпуклой функции будет глобальным экстремумом.\\\ 7) Для выпуклых функций выполняется неравенство Йенсена: 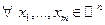
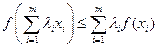 при
при 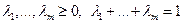 \\\Доказательство 7): при m=2 это есть определение выпуклости. Докажем по индукции.\\\\Пусть верно при m=n-1, то есть
\\\Доказательство 7): при m=2 это есть определение выпуклости. Докажем по индукции.\\\\Пусть верно при m=n-1, то есть 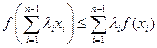 .\\\Покажем, что верно для m=n:
.\\\Покажем, что верно для m=n: 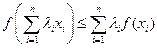 \\\Если
\\\Если 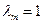 - очевидно, пусть
- очевидно, пусть 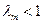 . \\\
. \\\ 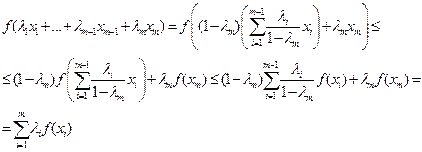 Также для выпуклых функций справедливы следующие неравенства.
Также для выпуклых функций справедливы следующие неравенства.
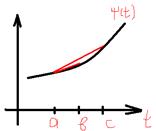
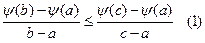 Доказательство: \\\
Доказательство: \\\ 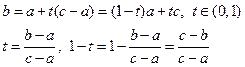 \\\По свойству выпуклости:
\\\По свойству выпуклости:
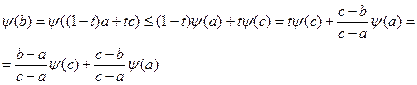 \\\Вычтем из обеих частей неравенства
\\\Вычтем из обеих частей неравенства 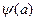 :\\\
:\\\ 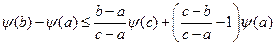 \\\
\\\ 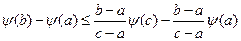
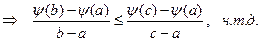 \\\ Второе
\\\ Второе 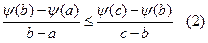 \\\Доказательство:\\\Из (1):
\\\Доказательство:\\\Из (1): 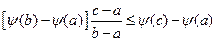 \\\\
\\\\ 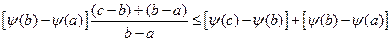 \\\
\\\ 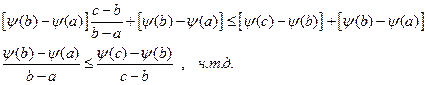 \\\\
\\\\ 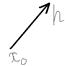 \\\Если f – дифференцируемая функция, то производная в точке
\\\Если f – дифференцируемая функция, то производная в точке 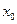 по направлению h равна скалярному произведению градиента в точке
по направлению h равна скалярному произведению градиента в точке 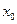 и вектора приращения: \\\
и вектора приращения: \\\ 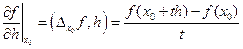 \\\\Теорема. f – дифференцируемая функция,\\\
\\\\Теорема. f – дифференцируемая функция,\\\ 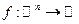 . f выпуклая
. f выпуклая 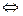
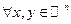 \\\\
\\\\ 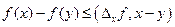 (
(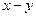 - вектор приращения)\\\Доказательство.\\\ 1)
- вектор приращения)\\\Доказательство.\\\ 1)  f – выпуклая, дифференцируемая функция
f – выпуклая, дифференцируемая функция 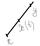 \\\
\\\ 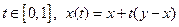 \\\
\\\ 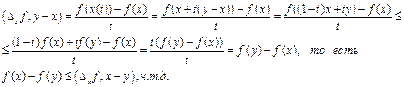 2)
2) 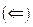
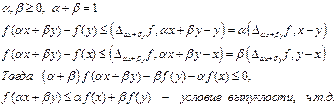 \\\\
\\\\ 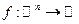 - выпуклая функция,
- выпуклая функция, 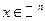
\\\\Рассмотрим вектор g: 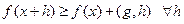 , g – субградиент функции f в точке x \\\
, g – субградиент функции f в точке x \\\ 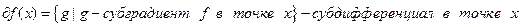 \\\Пример: функция
\\\Пример: функция 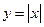
3. 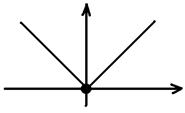 Ее субдифференциал
Ее субдифференциал 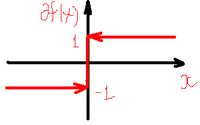 \\\Теорема.
\\\Теорема. 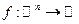 - выпуклая функция,
- выпуклая функция, 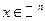 \\\Тогда в каждой точке x субдифференциал
\\\Тогда в каждой точке x субдифференциал 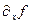 есть выпуклый компакт
есть выпуклый компакт  в
в 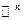 \\\Пусть
\\\Пусть 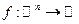 - выпуклая функция,\\\\
- выпуклая функция,\\\\ 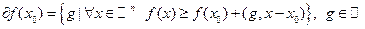 - субдифференциал в точке
- субдифференциал в точке 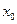 \\\Тогда выполняется:\\\ 1)
\\\Тогда выполняется:\\\ 1) 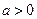 ,
, 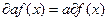 \\\ 2)
\\\ 2) 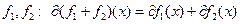 (теорема Моро-Рокофелара)\\\ 3)
(теорема Моро-Рокофелара)\\\ 3) 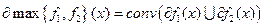 (теорема Дубовицкого-Мимотина)\\\ 4) Исследование на экстремум:
(теорема Дубовицкого-Мимотина)\\\ 4) Исследование на экстремум: 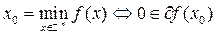 (теорема Ферма) 3)Задачи выпуклого программирования, DEF. Множество S
(теорема Ферма) 3)Задачи выпуклого программирования, DEF. Множество S 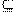 En называется выпуклым, если для любых двух точек
En называется выпуклым, если для любых двух точек 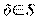 и
и 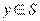 имеем
имеем 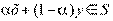 при любом
при любом 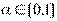 .\\\ Геометрически это означает, что вместе с
.\\\ Геометрически это означает, что вместе с 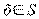 и
и 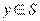 и весь отрезок
и весь отрезок 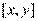 принадлежит множеству
принадлежит множеству 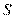 . Отметим, что отрезок
. Отметим, что отрезок 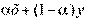 называется выпуклой комбинацией точек
называется выпуклой комбинацией точек 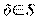 и
и 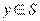 . \\\DEF. Функция f(x), заданная на выпуклом множестве X
. \\\DEF. Функция f(x), заданная на выпуклом множестве X 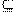 En, называется выпуклой на X, если для двух любых
En, называется выпуклой на X, если для двух любых 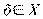 и
и 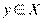 имеем
имеем 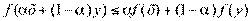 при любом
при любом 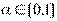 .\\\График выпуклой функции лежит ниже хорды, соединяющей его точки.
.\\\График выпуклой функции лежит ниже хорды, соединяющей его точки.

\\\DEF. Функция f(x), заданная на выпуклом множестве X 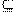 En, называется строго выпуклой на X, если для двух любых
En, называется строго выпуклой на X, если для двух любых 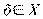 и
и 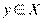 имеем
имеем 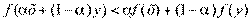 при любом
при любом 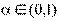 . \\\DEF. Функция f(x), заданная на выпуклом множестве X
. \\\DEF. Функция f(x), заданная на выпуклом множестве X  En, называется вогнутой на X, если функция – f(x) выпукла на X. \\Свойства выпуклых функций. Пусть функции f(x) и g(x) выпуклы на выпуклом множестве X
En, называется вогнутой на X, если функция – f(x) выпукла на X. \\Свойства выпуклых функций. Пусть функции f(x) и g(x) выпуклы на выпуклом множестве X  En. Тогда: \\\1) Функции f(x) + g(x) и max { f(x), g(x) } выпуклы на X. \\\2) Функция cf(x) выпукла на X при c ≥0. \\\3) Функция f(x) непрерывна на
En. Тогда: \\\1) Функции f(x) + g(x) и max { f(x), g(x) } выпуклы на X. \\\2) Функция cf(x) выпукла на X при c ≥0. \\\3) Функция f(x) непрерывна на 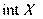 (см. рис. 3.8). 4) \\\Множество
(см. рис. 3.8). 4) \\\Множество 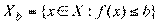 является выпуклым множеством при любом числе b. \\\DEF. Надграфиком (эпиграфом) выпуклой функции f(x), определенной на выпуклом множестве X
является выпуклым множеством при любом числе b. \\\DEF. Надграфиком (эпиграфом) выпуклой функции f(x), определенной на выпуклом множестве X 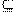 En, называется n +1-мерное множество epi f, определяемое так:
En, называется n +1-мерное множество epi f, определяемое так: 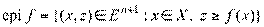 \\\Понятие надграфика проиллюстрировано на рис. 3.10. \\\Свойство надграфика. Выпуклость надграфика функции f(x), определенной на выпуклом множестве X, эквивалентна выпуклости функции. \\\DEF. Под задачей выпуклого программирования будем понимать задачу
\\\Понятие надграфика проиллюстрировано на рис. 3.10. \\\Свойство надграфика. Выпуклость надграфика функции f(x), определенной на выпуклом множестве X, эквивалентна выпуклости функции. \\\DEF. Под задачей выпуклого программирования будем понимать задачу
F (х)→ max при х ∈ X ={ х ∈ Еп: gj(x)≤bj, j=1,2,…,m, x ≥0}, \\\где функция F (х) – вогнута, а функции gj(x), j=1,2,…,m – выпуклы. Напомним, что последнее условие приводит к выпуклости множества X (см. свойство 4 выпуклых функций). \\\Имеют место несколько важнейших свойств задач выпуклого программирования, которое определяет их роль в теории оптимизации .\\\Теорема 1. Множество точек X* 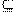 X, на которых достигается глобальный максимум F (х) в задаче выпуклого программирования, является выпуклым.
X, на которых достигается глобальный максимум F (х) в задаче выпуклого программирования, является выпуклым.
Замечание. Множество X* может быть и пусто.\\\ Доказательство теоремы сразу следует из выпуклости множества X и определения вогнутости функции F (х). \\\Теорема 2. («локально-глобальная»). Пусть функция 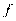 (х) вогнута на выпуклом множестве X. Тогда любой локальный максимум является глобальным. \\\Теорема 3. Если при выполнении условий теоремы 2 функция f (х) строго вогнута, то глобальный максимум является единственным. \\\Седловая точка функции Лагранжа. Теорема Куна-Таккера \\\Рассмотрим функцию Лагранжа
(х) вогнута на выпуклом множестве X. Тогда любой локальный максимум является глобальным. \\\Теорема 3. Если при выполнении условий теоремы 2 функция f (х) строго вогнута, то глобальный максимум является единственным. \\\Седловая точка функции Лагранжа. Теорема Куна-Таккера \\\Рассмотрим функцию Лагранжа 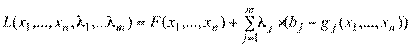 \\\для задачи максимизации F(х)→ max при gj(x) ≤ bj, j = 1,2,…,m; x ≥ 0. \\\Напомним, что функция Лагранжа для задачи нелинейного программирования задана при x
\\\для задачи максимизации F(х)→ max при gj(x) ≤ bj, j = 1,2,…,m; x ≥ 0. \\\Напомним, что функция Лагранжа для задачи нелинейного программирования задана при x  0 и λ
0 и λ  0. \\\DEF. Точка (x *, λ*), где x *
0. \\\DEF. Точка (x *, λ*), где x * 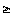 0 и λ*
0 и λ* 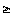 0, называется седловой точкой функции Лагранжа, если L (x, λ*)
0, называется седловой точкой функции Лагранжа, если L (x, λ*) 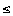 L (x *, λ*)
L (x *, λ*) 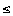 L (x *, λ) для всех x
L (x *, λ) для всех x 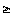 0 и λ
0 и λ 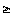 0.\\\Основным результатом является теорема Куна-Таккера и ее использование для анализа и решения задач выпуклого программирования. Существенным элементом теоремы Куна-Таккера является выполнение условия Слейтера. \\\Условие Слейтера. Существует такая допустимая точка
0.\\\Основным результатом является теорема Куна-Таккера и ее использование для анализа и решения задач выпуклого программирования. Существенным элементом теоремы Куна-Таккера является выполнение условия Слейтера. \\\Условие Слейтера. Существует такая допустимая точка 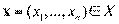 , в которой все нелинейные (функциональные) ограничения выполняются как строгие неравенства
, в которой все нелинейные (функциональные) ограничения выполняются как строгие неравенства 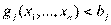 .
.
Отметим, что в условии Слейтера в точке х 0∈ X лишь нелинейные функциональный ограничения gj (x 0) ≤ bj, j=1,2,…,m, должны выполняться в виде строгих неравенств. \\\Теорема Куна-Таккера. Пусть в задаче выпуклого программирования множество X удовлетворяет условию Слейтера. Тогда для того, чтобы вектор х * являлся решением задачи выпуклого программирования, необходимо и достаточно, чтобы нашелся такой вектор λ* 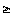 0, что пара (x *, λ *) составляет седловую точку функции Лагранжа, т.е. L(x, λ*)
0, что пара (x *, λ *) составляет седловую точку функции Лагранжа, т.е. L(x, λ*) 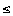 L(x*, λ*)
L(x*, λ*) 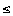 L(x*, λ) для всех x
L(x*, λ) для всех x 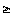 0 и λ
0 и λ 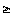 0. \\\Двойственные задачи нелинейного программирования. Экономическая интерпретация: рыночное равновесие. Пусть имеем задачу нелинейного программирования в виде:
0. \\\Двойственные задачи нелинейного программирования. Экономическая интерпретация: рыночное равновесие. Пусть имеем задачу нелинейного программирования в виде:
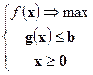 (1)\\\Составим функцию Лагранжа для этой задачи:
(1)\\\Составим функцию Лагранжа для этой задачи: 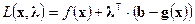 .\\\Назовем
.\\\Назовем 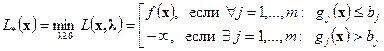 – прямой функцией, а
– прямой функцией, а 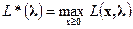 – двойственной функцией задачи (1), а задачи нахождения
– двойственной функцией задачи (1), а задачи нахождения 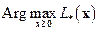 и
и 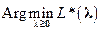 соответственно прямой и двойственной задачами.\\\Функция Лагранжа, двойственные функции и факт существования седловой точки имеют различные экономические интерпретации. Наиболее интересная интерпретация связана с конкурентным взаимодействием между некоторой отраслью промышленности и рынком: \\\Отрасль промышленности производит некоторую продукцию и реализует ее на рынке. Она стремится максимизировать свою прибыль путем определения оптимального объема производства товаров. Рынок противодействует этой цели, устанавливая свои цены на сырье, которое отрасль промышленности приобретает на рынке для обеспечения производства товаров.\\\Пусть: \\\
соответственно прямой и двойственной задачами.\\\Функция Лагранжа, двойственные функции и факт существования седловой точки имеют различные экономические интерпретации. Наиболее интересная интерпретация связана с конкурентным взаимодействием между некоторой отраслью промышленности и рынком: \\\Отрасль промышленности производит некоторую продукцию и реализует ее на рынке. Она стремится максимизировать свою прибыль путем определения оптимального объема производства товаров. Рынок противодействует этой цели, устанавливая свои цены на сырье, которое отрасль промышленности приобретает на рынке для обеспечения производства товаров.\\\Пусть: \\\ 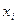 - количество (объем) товара вида
- количество (объем) товара вида 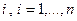 , которое отрасль планирует произвести и реализовать на рынке в рассматриваемый период времени Т;\\\
, которое отрасль планирует произвести и реализовать на рынке в рассматриваемый период времени Т;\\\ 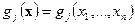 - количество сырья вида
- количество сырья вида 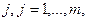 которое необходимо для производства планируемого количества товаров
которое необходимо для производства планируемого количества товаров 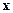 ;\\\
;\\\ 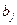 - количество сырья вида
- количество сырья вида 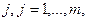 которое уже имеется у отрасли (запас, сырье приобретенное до рассматриваемого периода времени Т, за него уже уплачено ранее по прежней цене);\\\
которое уже имеется у отрасли (запас, сырье приобретенное до рассматриваемого периода времени Т, за него уже уплачено ранее по прежней цене);\\\ 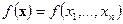 - доход, который отрасль может получить от реализации произведенных товаров в количестве
- доход, который отрасль может получить от реализации произведенных товаров в количестве 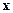 с учетом цен, установившихся на рынке в рассматриваемый период Т;\\\
с учетом цен, установившихся на рынке в рассматриваемый период Т;\\\ 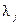 - цена на сырье вида
- цена на сырье вида 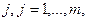 устанавливаемая рынком на рассматриваемый период времени Т.\\Если отрасли для производства товаров в количестве
устанавливаемая рынком на рассматриваемый период времени Т.\\Если отрасли для производства товаров в количестве 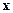 хватает сырья вида
хватает сырья вида 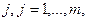 т.е.
т.е. 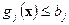 , то она не закупает его на рынке, а если остаются излишки
, то она не закупает его на рынке, а если остаются излишки 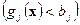 , продает соответствующий вид сырья по рыночной цене
, продает соответствующий вид сырья по рыночной цене 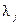 , получая дополнительный доход в размере
, получая дополнительный доход в размере  . Если же данного вида сырья не хватает
. Если же данного вида сырья не хватает 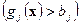 , отрасль закупает его на рынке по той же цене
, отрасль закупает его на рынке по той же цене 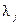 и несет расходы в размере
и несет расходы в размере 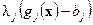 , или, что то же самое, получает отрицательный доход, равный
, или, что то же самое, получает отрицательный доход, равный  .\\\Из сказанного следует, что прибыль отрасли (без учета прочих издержек) составляет
.\\\Из сказанного следует, что прибыль отрасли (без учета прочих издержек) составляет 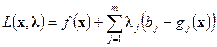 . Эта же величина равна издержкам рынка, связанным с закупкой продукции отрасли и излишков сырья (отрицательные слагаемые из суммы идут в доход рынка).
. Эта же величина равна издержкам рынка, связанным с закупкой продукции отрасли и излишков сырья (отрицательные слагаемые из суммы идут в доход рынка).
Таким образом, имеет место игровая ситуация, при которой отрасль хочет максимизировать функцию Лагранжа, а рынок – минимизировать. При этом отрасль может управлять переменной 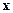 , а рынок – переменной
, а рынок – переменной 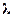 .\\\Из сказанного следует, что отрасль формирует двойственную функцию
.\\\Из сказанного следует, что отрасль формирует двойственную функцию 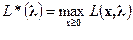 , а рынок – прямую:
, а рынок – прямую: 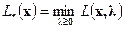 .\\\Если имеет место равенство
.\\\Если имеет место равенство 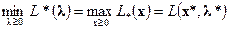 , то в такой седловой точке
, то в такой седловой точке 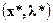 достигается экономическое конкурентное равновесие. Это означает, что, во-первых, при заданном уровне цен на сырье
достигается экономическое конкурентное равновесие. Это означает, что, во-первых, при заданном уровне цен на сырье 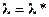 никакое изменение объема производства отрасли (отклонение от
никакое изменение объема производства отрасли (отклонение от 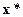 ) не может увеличить ее прибыль и, во-вторых, при заданном объеме производства
) не может увеличить ее прибыль и, во-вторых, при заданном объеме производства 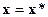 никакое изменение цен на сырье (отклонение от
никакое изменение цен на сырье (отклонение от 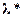 ) не может уменьшить прибыль отрасли, или, что то же самое, издержек рынка. Таким образом, состояние равновесия приводит к устойчивому рынку.\\\Множители Лагранжа
) не может уменьшить прибыль отрасли, или, что то же самое, издержек рынка. Таким образом, состояние равновесия приводит к устойчивому рынку.\\\Множители Лагранжа 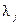 часто называют двойственными переменными, теневыми ценами, приписанными оценками или объективно обусловленными оценками. №4. Задачи линейного программирования. Симплекс метод. Задача линейного программирования состоит в определении максимального (минимального) значения целевой функции при некоторых условиях (и функция, и условия линейны).\\\Стандартная задача линейного программирования:
часто называют двойственными переменными, теневыми ценами, приписанными оценками или объективно обусловленными оценками. №4. Задачи линейного программирования. Симплекс метод. Задача линейного программирования состоит в определении максимального (минимального) значения целевой функции при некоторых условиях (и функция, и условия линейны).\\\Стандартная задача линейного программирования: 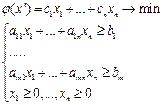
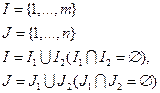 \\\Общая задача лин. программирования:
\\\Общая задача лин. программирования: 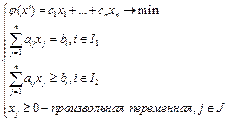 \\Рассмотрим стандартную задачу линейного программирования, где X – множество ограничений.\\\\Замечание: выполнены следующие условия:
\\Рассмотрим стандартную задачу линейного программирования, где X – множество ограничений.\\\\Замечание: выполнены следующие условия: 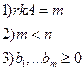 \\\В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.\\\Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.\\\Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные X1, X2,..., Xr, то решение {b1, b2,..., br, 0,..., 0} будет опорным при условии, что b1, b2,..., br ≥ 0.\\\Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом. \\\ Известно, что
\\\В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.\\\Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.\\\Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные X1, X2,..., Xr, то решение {b1, b2,..., br, 0,..., 0} будет опорным при условии, что b1, b2,..., br ≥ 0.\\\Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом. \\\ Известно, что  -крайняя точка X тогда и только тогда, когда столбцы матрицы А, отвечающие строго положительным координатам точки
-крайняя точка X тогда и только тогда, когда столбцы матрицы А, отвечающие строго положительным координатам точки  линейно независимы.\\\ Теорема 1: Если
линейно независимы.\\\ Теорема 1: Если 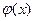 принимает минимальное значение в некоторой точке X, то
принимает минимальное значение в некоторой точке X, то 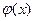 принимает это значение в некоторой крайней точке множества X.\\\ Теорема 2: Если множество X не пусто, то множество крайних точек так же не пусто, то есть X имеет крайнюю точку.\\\Если
принимает это значение в некоторой крайней точке множества X.\\\ Теорема 2: Если множество X не пусто, то множество крайних точек так же не пусто, то есть X имеет крайнюю точку.\\\Если 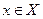 - крайняя точка, то она невырождена, если имеет
- крайняя точка, то она невырождена, если имеет 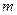 положительных координат. Задача лин. программирования невырождена, если все крайние точки X невырождены.\\\ \\Симплекс-метод. – см выше №5.Задачи линейного программирования. Двойственность. \\\Задачей линейного программирования называется задача отыскания экстремума (максимума или минимума) линейной функции от нескольких переменных при линейных ограничениях на эти переменные. Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств. Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. \\\ Математическая формулировка задачи линейного программирования \\\Нужно определить максимум линейной целевой функции (линейной формы)
положительных координат. Задача лин. программирования невырождена, если все крайние точки X невырождены.\\\ \\Симплекс-метод. – см выше №5.Задачи линейного программирования. Двойственность. \\\Задачей линейного программирования называется задача отыскания экстремума (максимума или минимума) линейной функции от нескольких переменных при линейных ограничениях на эти переменные. Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств. Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. \\\ Математическая формулировка задачи линейного программирования \\\Нужно определить максимум линейной целевой функции (линейной формы)
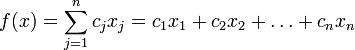 \\\\при условиях
\\\\при условиях 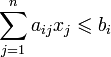 при
при 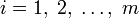 .\\\Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя её во всех остальных равенствах и неравенствах (а также в функции f). \\\\ Транспортная задача \\\Имеется некий однородный груз, который нужно перевести с n складов на m заводов. Для каждого склада i известно, сколько в нём находится груза ai, а для каждого завода известна его потребность bj в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния cij от i -го склада до j -го завода известны). Требуется составить наиболее дешёвый план перевозки.\\\Решающими переменными в данном случае являются xij — количества груза, перевезённого из i -го склада на j -й завод. Они удовлетворяют ограничениям:\\\
.\\\Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя её во всех остальных равенствах и неравенствах (а также в функции f). \\\\ Транспортная задача \\\Имеется некий однородный груз, который нужно перевести с n складов на m заводов. Для каждого склада i известно, сколько в нём находится груза ai, а для каждого завода известна его потребность bj в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния cij от i -го склада до j -го завода известны). Требуется составить наиболее дешёвый план перевозки.\\\Решающими переменными в данном случае являются xij — количества груза, перевезённого из i -го склада на j -й завод. Они удовлетворяют ограничениям:\\\ 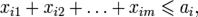 \\\
\\\ 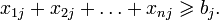 \\\Целевая функция имеет вид:
\\\Целевая функция имеет вид: 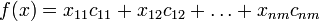 , которую надо минимизировать.\\\ Прямая и двойчтвенная задачи \\\Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой. Связь исходной и двойственной задач заключается главным образом в том, что решение одной из них может быть получено непосредственно из решения другой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования
, которую надо минимизировать.\\\ Прямая и двойчтвенная задачи \\\Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой. Связь исходной и двойственной задач заключается главным образом в том, что решение одной из них может быть получено непосредственно из решения другой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования
| Исходная задача | Двойственная задача |
1. 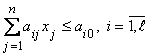 | 1'. 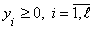 |
2. 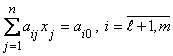 | 2'. 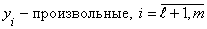 |
3. 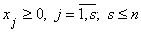 | 3'. 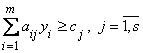 |
4. 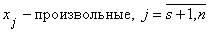 | 4'. 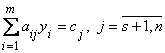 |
5. 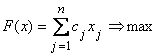 | 5'. 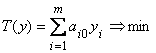 |
Таблица 11.1
\\\СВЯЗЬ МЕЖДУ РЕШЕНИЯМИ ПРЯМОЙ И ДВОЙСТВЕННОЙ ЗАДАЧ\\\Лемма 11.1 Если 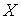 – некоторый план исходной задачи, а
– некоторый план исходной задачи, а 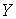 – произвольный план двойственной задачи, то значение целевой функции исходной задачи при плане
– произвольный план двойственной задачи, то значение целевой функции исходной задачи при плане 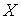 всегда не превосходит значение целевой функции двойственной задачи при плане
всегда не превосходит значение целевой функции двойственной задачи при плане 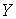 , т.е.
, т.е. 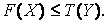 \\\ Лемма 11.2. Если
\\\ Лемма 11.2. Если 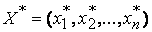 и
и 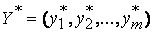 – допустимые решения взаимно двойственных задач, для которых выполняется равенство
– допустимые решения взаимно двойственных задач, для которых выполняется равенство 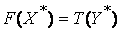 , то
, то 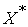 – оптимальное решение исходной задачи, а
– оптимальное решение исходной задачи, а 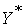 – оптимальное решение двойственной задачи. \\\ Теорема 11.1. Первая теорема двойственности. Если одна из пары двойственных задач имеет оптимальный план
– оптимальное решение двойственной задачи. \\\ Теорема 11.1. Первая теорема двойственности. Если одна из пары двойственных задач имеет оптимальный план 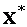 , то и другая имеет оптимальный план
, то и другая имеет оптимальный план 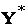 и значения целевых функций задач при их оптимальных планах равны между собой, т. е. \\\\
и значения целевых функций задач при их оптимальных планах равны между собой, т. е. \\\\ 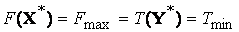 . \\\Если же целевая функция одной из пары двойственных задач не ограничена (для исходной – сверху, для двойственной – снизу), то область допустимых решений другой задачи пустая. \\\Из этой теоремы вытекают необходимые и достаточные условия:\\\a) разрешимости задач – существование хотя бы одного допустимого плана у каждой задачи;\\\б) оптимальности допустимых планов X и Y – выполнение равенства F (X) = T (Y). \\\Теорема 11.2. Вторая теорема двойственности. Для того чтобы два допустимых решения
. \\\Если же целевая функция одной из пары двойственных задач не ограничена (для исходной – сверху, для двойственной – снизу), то область допустимых решений другой задачи пустая. \\\Из этой теоремы вытекают необходимые и достаточные условия:\\\a) разрешимости задач – существование хотя бы одного допустимого плана у каждой задачи;\\\б) оптимальности допустимых планов X и Y – выполнение равенства F (X) = T (Y). \\\Теорема 11.2. Вторая теорема двойственности. Для того чтобы два допустимых решения 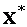 и
и 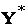 пары двойственных задач были их оптимальными решениями, необходимо и достаточно, чтобы они удовлетворяли системе уравнений
пары двойственных задач были их оптимальными решениями, необходимо и достаточно, чтобы они удовлетворяли системе уравнений
 (*)
(*) 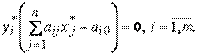 (**) \\\ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД\\\ Из результатов предыдущих пунктов следует, что для получения решения исходной задачи можно перейти к двойственной и, используя оценки ее оптимального плана, определить оптимальное решение исходной задачи\\\Как было показано, при решении прямой задачи на любой итерации разность
(**) \\\ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД\\\ Из результатов предыдущих пунктов следует, что для получения решения исходной задачи можно перейти к двойственной и, используя оценки ее оптимального плана, определить оптимальное решение исходной задачи\\\Как было показано, при решении прямой задачи на любой итерации разность 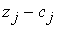 , т.е. величина
, т.е. величина 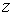 -коэффициента при переменной
-коэффициента при переменной 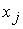 , равна разности между правой и левой частями соответствующего ограничения двойственной задачи. Если при решении прямой задачи с максимизируемой целевой функцией итерация не приводит к оптимальному решению, то по крайней мере для одной переменной
, равна разности между правой и левой частями соответствующего ограничения двойственной задачи. Если при решении прямой задачи с максимизируемой целевой функцией итерация не приводит к оптимальному решению, то по крайней мере для одной переменной 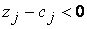 и только в оптимуме для всех
и только в оптимуме для всех 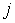 разность
разность 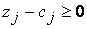 .\\\Рассматривая это условие с учетом двойственности, можно записать\\\
.\\\Рассматривая это условие с учетом двойственности, можно записать\\\ 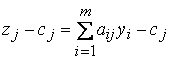 .\\\Таким образом, если
.\\\Таким образом, если 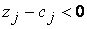 , то
, то 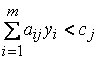 . Это означает, что, когда решение прямой задачи неоптимальное, решение двойственной задачи недопустимое. С другой стороны
. Это означает, что, когда решение прямой задачи неоптимальное, решение двойственной задачи недопустимое. С другой стороны 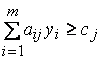 при
при 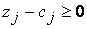 . Отсюда следует, что оптимальному решению прямой задачи соответствует допустимое решение двойственной задачи.\\\Это позволило разработать новый метод решения задач линейного программирования, при использовании которого сначала получается недопустимое, но «лучшее, чем оптимальное» решение (в обычном симплекс-методе сначала находится допустимое, но неоптимальное решение). Новый метод, получивший название двойственного симплекс-метода, обеспечивает выполнение условия оптимальности решения и систематическое «приближение» его к области допустимых решений. Когда полученное решение оказывается допустимым, итерационный процесс вычислений заканчивается, так как это решение является и оптимальным.\\\Двойственный симплекс-метод позволяет решать задачи линейного программирования, системы ограничений которых при положительном базисе содержат свободные члены любого знака. Этот метод позволяет уменьшить количество преобразований системы ограничений, а также размера симплексной таблицы. Рассмотрим применение двойственного симплекс-метода на примере. №6. Постановка задач целочисленного программирования. \\\ Задача целочисленного программирования.\\\
. Отсюда следует, что оптимальному решению прямой задачи соответствует допустимое решение двойственной задачи.\\\Это позволило разработать новый метод решения задач линейного программирования, при использовании которого сначала получается недопустимое, но «лучшее, чем оптимальное» решение (в обычном симплекс-методе сначала находится допустимое, но неоптимальное решение). Новый метод, получивший название двойственного симплекс-метода, обеспечивает выполнение условия оптимальности решения и систематическое «приближение» его к области допустимых решений. Когда полученное решение оказывается допустимым, итерационный процесс вычислений заканчивается, так как это решение является и оптимальным.\\\Двойственный симплекс-метод позволяет решать задачи линейного программирования, системы ограничений которых при положительном базисе содержат свободные члены любого знака. Этот метод позволяет уменьшить количество преобразований системы ограничений, а также размера симплексной таблицы. Рассмотрим применение двойственного симплекс-метода на примере. №6. Постановка задач целочисленного программирования. \\\ Задача целочисленного программирования.\\\ 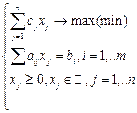 \\\При решении многих задач нецелочисленное программирование не имеет смысла, попытка округления до целых значений приводит либо к нарушению ограничений задачи, либо к недоиспользованию ресурсов.\\\В случае двухмерной задачи проблема решается относительно просто путем выявления всех целочисленных точек, близких к границе множества планов, построения «выпуклой целочисленной оболочки» (выпуклого множества планов, содержащего все целочисленные планы) и решения задачи над этим множеством.\\\Методы решения задач целочисленного программирования можно классифицировать как методы отсечения и комбинаторные методы. \\\Метод Гомори относится к методам отсечения. В общем случае выдвигается идея последовательного отсечения нецелочисленных оптимальных планов: обычным симплексным методом отыскивается оптимальный план и, если он нецелочисленный, строится дополнительное ограничение, отсекающее найденный оптимальный план, но не отсекающее ни одного целочисленного плана. \\\Метод Гомори (метод отсечений). \\\Рассматриваются задачи
\\\При решении многих задач нецелочисленное программирование не имеет смысла, попытка округления до целых значений приводит либо к нарушению ограничений задачи, либо к недоиспользованию ресурсов.\\\В случае двухмерной задачи проблема решается относительно просто путем выявления всех целочисленных точек, близких к границе множества планов, построения «выпуклой целочисленной оболочки» (выпуклого множества планов, содержащего все целочисленные планы) и решения задачи над этим множеством.\\\Методы решения задач целочисленного программирования можно классифицировать как методы отсечения и комбинаторные методы. \\\Метод Гомори относится к методам отсечения. В общем случае выдвигается идея последовательного отсечения нецелочисленных оптимальных планов: обычным симплексным методом отыскивается оптимальный план и, если он нецелочисленный, строится дополнительное ограничение, отсекающее найденный оптимальный план, но не отсекающее ни одного целочисленного плана. \\\Метод Гомори (метод отсечений). \\\Рассматриваются задачи 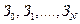 . Ограничения задачи
. Ограничения задачи 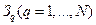 получаются добавлением к ограничениям предыдущей задачи
получаются добавлением к ограничениям предыдущей задачи 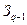 множества неравенств со следующими свойствами:\\\ 1) все целочисленные векторы допустимого множества
множества неравенств со следующими свойствами:\\\ 1) все целочисленные векторы допустимого множества 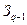 принадлежат допустимому множеству
принадлежат допустимому множеству 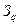 . \\\2) если
. \\\2) если 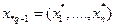 -не целочисленное решение задачи
-не целочисленное решение задачи 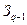 , то
, то 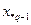 не принадлежит допустимому множеству задачи
не принадлежит допустимому множеству задачи 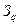 . Алгоритм:1) Задача
. Алгоритм:1) Задача 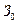 решается симплекс-методом.\\\ 2) Если задача
решается симплекс-методом.\\\ 2) Если задача 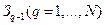 решена, тогда рассматривают последнюю таблицу симплекс-метода, дающее решение задачи:
решена, тогда рассматривают последнюю таблицу симплекс-метода, дающее решение задачи:
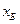 | 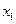 | ………… | 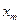 | 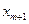 | ……….. | 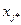 | ……. | 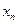 | |
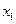 | ………… | 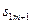 | ……….. | 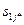 | ……. | 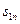 | 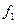 | ||
| ….. | ….. | ………… | ……. | …… | ………. | ….. | ……. | ….. | …… |
| ….. | …… | ………… | …….. | …… | ………. | …… | …… | …… | …… |
| …… | ……. | ………… | ……. | ……. | ……….. | …….. | ……. | ……. | ……. |
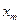 | ……….. | 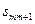 | ……….. |  | ……. | 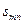 | 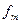 |
\\\В оптимальном плане выбирают строку, в которой целая часть дробного свободного члена принимает наибольшее значение: 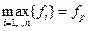 1) К ограничениям задачи добавляем неравенство, в котором коэффициенты будут дробными частями коэффициентов данного уравнения:
1) К ограничениям задачи добавляем неравенство, в котором коэффициенты будут дробными частями коэффициентов данного уравнения: 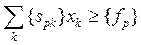 , где к- индексы небазисных переменных. 2) Переводим к каноническому виду, добавляя переменную
, где к- индексы небазисных переменных. 2) Переводим к каноническому виду, добавляя переменную 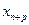 :
: 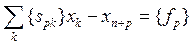 \\\\\ Соответственно добавляем новый базисный вектор по новой переменной
\\\\\ Соответственно добавляем новый базисный вектор по новой переменной 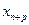 .\\\\Если полученная задача имеет целое решение, то заканчиваем. В противном случае переходим к первому пункту.\\\\Основные недостатки методов отсечений.\\\ 1). Ни один тип отсечений не обеспечивает высокой эффективности соответствующих вычислительных процедур.\\\\ 2) Методы отсечений не подходят для решения целочисленных задач больших размерностей. \\\\Метод ветвей и границ. \\\\В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений. Наиболее известным из них является метод ветвей и границ, который также опирается на процедуру решения задачи с ослабленными ограничениями. При таком подходе из рассматриваемой задачи получаются две подзадачи путем специального разбиения пространства решений и отбрасывания областей, не содержащих допустимых целочисленных решений. В случае, когда целочисленные переменные являются булевыми, применяются комбинаторные методы. \\\Общая идея метода может быть описана на примере поиска минимума и максимума функции f(x) на множестве допустимых значений x. Функция f и x могут быть произвольной природы. Для метода ветвей и границ необходимы две процедуры: ветвление и нахождение оценок (границ).\\\ 1) Процедура ветвления состоит в разбиении области допустимых решений на подобласти меньших размеров. Процедуру можно рекурсивно применять к подобластям. Полученные подобласти образуют дерево, называемое деревом поиска или деревом ветвей и границ. Узлами этого дерева являются построенные подобласти.\\\ 2) Процедура нахождения оценок заключается в поиске верхних и нижних границ для оптимального значения на подобласти допустимых решений.\\\В основе метода ветвей и границ лежит следующая идея: если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения (правило отсева). Обычно, минимальную из полученных верхних оценок записывают в глобальную переменную m; любой узел дерева поиска, нижняя граница которого больше значения m, может быть исключен из дальнейшего рассмотрения.\\\Если нижняя граница для узла дерева совпадает с верхней границей, то это значение является минимумом функции и достигается на соответствующей подобласти.\\\ Описание метода. \\\Рассматривается целочисленная задача максимизации функции при условиях. Многогранное множество, которое образуют условия, предполагается ограниченным. Как и в методах отсечения, процесс начинается с решения задачи линейного программирования. Если полученный при этом оптимальный план не удовлетворяет условиям целочисленности, то значение целевой функции на этом плане задает нижнюю границу для исходного оптимума. Пусть
.\\\\Если полученная задача имеет целое решение, то заканчиваем. В противном случае переходим к первому пункту.\\\\Основные недостатки методов отсечений.\\\ 1). Ни один тип отсечений не обеспечивает высокой эффективности соответствующих вычислительных процедур.\\\\ 2) Методы отсечений не подходят для решения целочисленных задач больших размерностей. \\\\Метод ветвей и границ. \\\\В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений. Наиболее известным из них является метод ветвей и границ, который также опирается на процедуру решения задачи с ослабленными ограничениями. При таком подходе из рассматриваемой задачи получаются две подзадачи путем специального разбиения пространства решений и отбрасывания областей, не содержащих допустимых целочисленных решений. В случае, когда целочисленные переменные являются булевыми, применяются комбинаторные методы. \\\Общая идея метода может быть описана на примере поиска минимума и максимума функции f(x) на множестве допустимых значений x. Функция f и x могут быть произвольной природы. Для метода ветвей и границ необходимы две процедуры: ветвление и нахождение оценок (границ).\\\ 1) Процедура ветвления состоит в разбиении области допустимых решений на подобласти меньших размеров. Процедуру можно рекурсивно применять к подобластям. Полученные подобласти образуют дерево, называемое деревом поиска или деревом ветвей и границ. Узлами этого дерева являются построенные подобласти.\\\ 2) Процедура нахождения оценок заключается в поиске верхних и нижних границ для оптимального значения на подобласти допустимых решений.\\\В основе метода ветвей и границ лежит следующая идея: если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения (правило отсева). Обычно, минимальную из полученных верхних оценок записывают в глобальную переменную m; любой узел дерева поиска, нижняя граница которого больше значения m, может быть исключен из дальнейшего рассмотрения.\\\Если нижняя граница для узла дерева совпадает с верхней границей, то это значение является минимумом функции и достигается на соответствующей подобласти.\\\ Описание метода. \\\Рассматривается целочисленная задача максимизации функции при условиях. Многогранное множество, которое образуют условия, предполагается ограниченным. Как и в методах отсечения, процесс начинается с решения задачи линейного программирования. Если полученный при этом оптимальный план не удовлетворяет условиям целочисленности, то значение целевой функции на этом плане задает нижнюю границу для исходного оптимума. Пусть 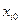 -целочисленная переменная, значение
-целочисленная переменная, значение 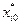 которой в оптимальном плане
которой в оптимальном плане 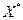 является дробным. Интервал
является дробным. Интервал 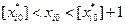 не содержит допустимых целочисленных компонентов решения. Поэтому в оптимальном плане значение
не содержит допустимых целочисленных компонентов решения. Поэтому в оптимальном плане значение 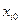 должно удовлетворять одному из неравенств
должно удовлетворять одному из неравенств 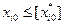 или
или 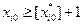 . Если границы изменения
. Если границы изменения 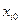 заранее не заданы, то их можно вычислить, решив для этого две вспомогательные задачи линейного программирования, заключающиеся в максимизации и минимизации
заранее не заданы, то их можно вычислить, решив для этого две вспомогательные задачи линейного программирования, заключающиеся в максимизации и минимизации 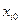 при первоначальных условиях (за исключением условия целочисленности). Введение их в задачу без учета условия целочисленности порождает две не связанные между собой задачи. В этом случае говорят, что задача разветвляется (или разбивается) на две подзадачи. Осуществляемый в процессе ветвления учет ограничения целочисленности позволяет исключить части многогранника допустимых решений, не содержащие точки с целыми координатами. \\\Если полученный оптимум оказывается допустимым для целочисленной задачи, такое решение следует зафиксировать как наилучшее. При этом нет необходимости продолжать ветвление подзадачи, поскольку улучшить найденное решение, очевидно, не удастся. В противном случае подзадача вновь разбивается на две подзадачи при условии целочисленности переменных, значение которых в оптимальном решении не являются целыми. Как только полученное допустимое целочисленное решение одной из подзадач оказывается лучше имеющегося, оно фиксируется вместо зарегистрированного ранее. Процесс ветвления продолжается до тех пор, пока каждая подзадача не приведет к целочисленному решению или пока не будет установлена возможность улучшения имеющегося решения. Зафиксированное допустимое решение и будет оптимальным.\\\Главный недостаток алгоритма метода ветвей и границ заключается в необходимости полностью решать задачи линейного программирования, ассоциированные с каждой из вершин многогранника допустимых решений. Для задач большой размерности это требует значительных и, неоправданных с затрат времени. 8 Транспортные задачи – специальный класс задач линейного программирования, которые описывают перемещение какого-либо товара из пункта отправления в пункт назначения. Назначение транспортной задачи – определить объем перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, налагаемые на объемы грузов, имеющихся в пунктах отправления (предложения), и ограничения, учитывающие потребность грузов пунктах назначения (спрос). \\\Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными.\\\\Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку).\\\\Описание\\\\
при первоначальных условиях (за исключением условия целочисленности). Введение их в задачу без учета условия целочисленности порождает две не связанные между собой задачи. В этом случае говорят, что задача разветвляется (или разбивается) на две подзадачи. Осуществляемый в процессе ветвления учет ограничения целочисленности позволяет исключить части многогранника допустимых решений, не содержащие точки с целыми координатами. \\\Если полученный оптимум оказывается допустимым для целочисленной задачи, такое решение следует зафиксировать как наилучшее. При этом нет необходимости продолжать ветвление подзадачи, поскольку улучшить найденное решение, очевидно, не удастся. В противном случае подзадача вновь разбивается на две подзадачи при условии целочисленности переменных, значение которых в оптимальном решении не являются целыми. Как только полученное допустимое целочисленное решение одной из подзадач оказывается лучше имеющегося, оно фиксируется вместо зарегистрированного ранее. Процесс ветвления продолжается до тех пор, пока каждая подзадача не приведет к целочисленному решению или пока не будет установлена возможность улучшения имеющегося решения. Зафиксированное допустимое решение и будет оптимальным.\\\Главный недостаток алгоритма метода ветвей и границ заключается в необходимости полностью решать задачи линейного программирования, ассоциированные с каждой из вершин многогранника допустимых решений. Для задач большой размерности это требует значительных и, неоправданных с затрат времени. 8 Транспортные задачи – специальный класс задач линейного программирования, которые описывают перемещение какого-либо товара из пункта отправления в пункт назначения. Назначение транспортной задачи – определить объем перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, налагаемые на объемы грузов, имеющихся в пунктах отправления (предложения), и ограничения, учитывающие потребность грузов пунктах назначения (спрос). \\\Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными.\\\\Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку).\\\\Описание\\\\ 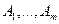 - поставщики\\\\
- поставщики\\\\ 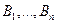 - потребители\\\
- потребители\\\ 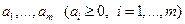 - запасы\\\
- запасы\\\ 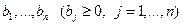 - потребности\\\\
- потребности\\\\ 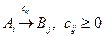 -цена перевозки единицы продукта\\\
-цена перевозки единицы продукта\\\ 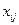 - количество продукта
- количество продукта 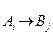 \\\(*)
\\\(*) 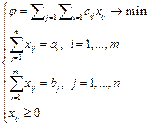 \\\(*) разрешима
\\\(*) разрешима 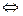
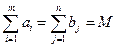
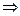 если
если 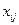 - решение, то
- решение, то 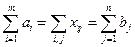 \\\В сбалансированной задаче есть m+n-1 линейно независимых переменных. Если все они больше нуля, то задача невырожденная (иначе - вырожденная).\\\\Требуется определить опорный план и путем последовательных операций найти оптимальное решение. (Сначала находится опорный план - базисное решение, затем он улучшается итерационно до нахождения оптимального плана). Пример 1. (
\\\В сбалансированной задаче есть m+n-1 линейно независимых переменных. Если все они больше нуля, то задача невырожденная (иначе - вырожденная).\\\\Требуется определить опорный план и путем последовательных операций найти оптимальное решение. (Сначала находится опорный план - базисное решение, затем он улучшается итерационно до нахождения оптимального плана). Пример 1. (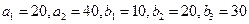 - задача сбалансирована(20+40=10+20+30)\\\
- задача сбалансирована(20+40=10+20+30)\\\ 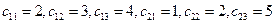
| B1=10 | B2=20 | B3=30 | |
| A1=20 | 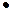 | ||
| A2=40 | 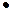 |
| В1=40 | В2=30 | В3=10 | В4=10 | В5=60 | |
| А1=40 | 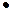 | 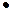 | 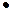 | ||
| А2=50 |  | ||||
| А3=50 |  |  |  |
 Сейчас читают про:
|
 2015-07-21
2015-07-21 3306
3306






