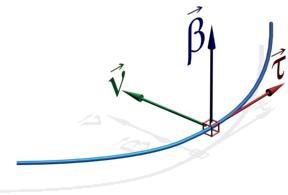
Определение 6.3. Прямую, проходящую через точку 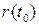 и имеющую направляющий вектор
и имеющую направляющий вектор 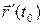 , будем называть касательной прямой в точке
, будем называть касательной прямой в точке 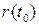 кривой
кривой 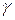 . Вектор
. Вектор 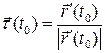 будем называть единичным вектором касательной.
будем называть единичным вектором касательной.
Определение 6.4. Плоскость, проходящая через точку 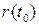 и имеющая направляющие векторы
и имеющая направляющие векторы 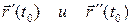 , называется соприкасающейся плоскостью кривой
, называется соприкасающейся плоскостью кривой 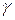 в точке
в точке 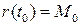 .
.
Упражнение 6.2. Определения 6.3 и 6.4 корректны, то есть не зависят от выбора параметризации.
Следствие 6.1. Какую бы параметризацию окрестности  точки
точки 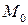 мы не взяли, ее вторая производная (это вектор-функция) лежит в соприкасающейся плоскости (точнее принадлежит ее направляющему пространству).
мы не взяли, ее вторая производная (это вектор-функция) лежит в соприкасающейся плоскости (точнее принадлежит ее направляющему пространству).
Более того, можно доказать, что, откладывая вторые производные различных параметризаций от точки 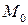 , мы будем получать точки одной и той же (относительно касательной прямой) полуплоскости соприкасающейся плоскости. Таким образом, направление вектора
, мы будем получать точки одной и той же (относительно касательной прямой) полуплоскости соприкасающейся плоскости. Таким образом, направление вектора 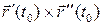 , идущего перпендикулярно соприкасающейся плоскости, не зависит от выбора параметризации. Вектор
, идущего перпендикулярно соприкасающейся плоскости, не зависит от выбора параметризации. Вектор 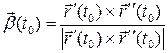 будем называть единичным вектором бинормали. Прямую, проходящую через точку
будем называть единичным вектором бинормали. Прямую, проходящую через точку 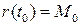 в направлении вектора
в направлении вектора 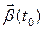 , будем называть бинормалью кривой
, будем называть бинормалью кривой 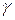 в точке
в точке 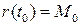 . Вектор же
. Вектор же 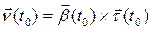 будем называть единичным вектором главной нормали, а прямую, проходящую через точку
будем называть единичным вектором главной нормали, а прямую, проходящую через точку 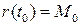 в направлении вектора
в направлении вектора 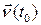 , будем называть главной нормалью кривой
, будем называть главной нормалью кривой 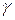 в точке
в точке 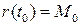 .
.
|
|
|
Таким образом, четверка 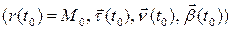 является правым ортонормированным репером. Этот репер называется репером Френе. Касательная прямая, главная нормаль и бинормаль являются координатными осями соответствующей координатной системы. Для координатных плоскостей этой координатной системы также есть названия. Как уже было сказано, плоскость, содержащая касательную и нормаль, называется соприкасающейся плоскость. Плоскость, содержащая главную нормаль и бинормаль, называется нормальной плоскостью. Плоскость же, содержащая касательную и бинормаль, называется спрямляющей плоскостью.
является правым ортонормированным репером. Этот репер называется репером Френе. Касательная прямая, главная нормаль и бинормаль являются координатными осями соответствующей координатной системы. Для координатных плоскостей этой координатной системы также есть названия. Как уже было сказано, плоскость, содержащая касательную и нормаль, называется соприкасающейся плоскость. Плоскость, содержащая главную нормаль и бинормаль, называется нормальной плоскостью. Плоскость же, содержащая касательную и бинормаль, называется спрямляющей плоскостью.
Пусть 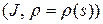 ‑ натуральная параметризация окрестности
‑ натуральная параметризация окрестности  точки
точки 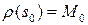 . Тогда, в силу леммы о вектор-функции постоянной длины, вектор
. Тогда, в силу леммы о вектор-функции постоянной длины, вектор 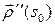 перпендикулярен
перпендикулярен 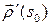 и, следовательно,
и, следовательно, 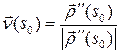 ‑ единичный вектор главной нормали. Осталось лишь заметить, что
‑ единичный вектор главной нормали. Осталось лишь заметить, что 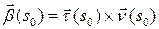 – единичный вектор бинормали.
– единичный вектор бинормали.
§7. Кривизна кривой
Пусть 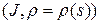 натуральная параметризация окрестности
натуральная параметризация окрестности  точки
точки 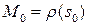 кривой
кривой 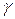 . Рассмотрим векторы
. Рассмотрим векторы 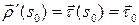 ;
; 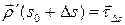 , обозначим
, обозначим 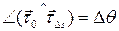 .
.
Определение 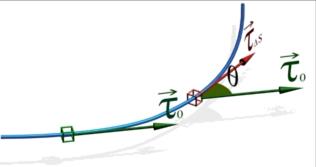 7.1. Величина
7.1. Величина 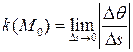 (скорость изменения угла) называется кривизной кривой в точке
(скорость изменения угла) называется кривизной кривой в точке 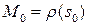 .
.
Так как 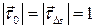 , то
, то
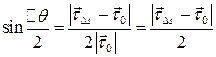
Значит 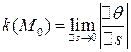
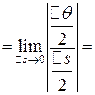
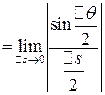
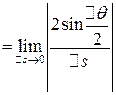 =
= 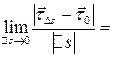
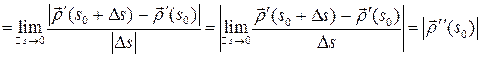 .
.
Таким образом
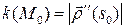
где 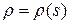 ‑ натуральная параметризация.
‑ натуральная параметризация.
Определение 7.2. Вектор 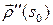 называют вектором кривизны кривой в точке
называют вектором кривизны кривой в точке 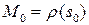 . Величина, обратная кривизне, называется радиусом кривизны кривой в соответствующей точке.
. Величина, обратная кривизне, называется радиусом кривизны кривой в соответствующей точке.
|
|
|
Пусть 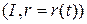 еще одна, теперь уже произвольная, параметризация окрестности
еще одна, теперь уже произвольная, параметризация окрестности  . Нетрудно заметить, что
. Нетрудно заметить, что
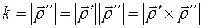
Здесь мы опустили аргументы и также учли, что 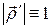 и что
и что 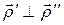 . Если
. Если 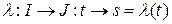 ‑ замена параметра, то,
‑ замена параметра, то, 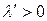 (так как мы рассматриваем ориентированные кривые, что, впрочем, для данного рассмотрения не ограничивает общность) и
(так как мы рассматриваем ориентированные кривые, что, впрочем, для данного рассмотрения не ограничивает общность) и 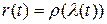 . Дважды дифференцируя последнее равенство, получаем:
. Дважды дифференцируя последнее равенство, получаем: 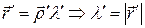 и
и 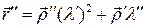 . Тогда
. Тогда 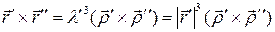 , откуда
, откуда 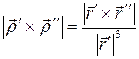 или, учитывая
или, учитывая
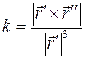
§8. Кручение кривой
 Пусть
Пусть 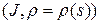 натуральная параметризация окрестности
натуральная параметризация окрестности  точки
точки 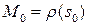 ориентированной кривой
ориентированной кривой 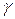 . Обозначим
. Обозначим 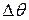 угол между векторами
угол между векторами 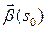 и
и 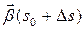 или, что то же самое, угол между соприкасающимися плоскостями в соответствующих точках (предполагается, что
или, что то же самое, угол между соприкасающимися плоскостями в соответствующих точках (предполагается, что 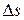 достаточно мало). При этом, если вектор бинормали повернулся в направлении к
достаточно мало). При этом, если вектор бинормали повернулся в направлении к 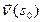 ‑ поворот, глядя с конца вектора
‑ поворот, глядя с конца вектора 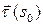 , произошел по часовой стрелке, будем считать угол отрицательным и говорить, что вращение произошло в отрицательном направлении. Если поворот произошел от
, произошел по часовой стрелке, будем считать угол отрицательным и говорить, что вращение произошло в отрицательном направлении. Если поворот произошел от 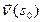 ‑ поворот, глядя с конца вектора
‑ поворот, глядя с конца вектора 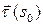 , произошел против часовой стрелки, то угол будем считать положительным и говорить, что вращение произошло в положительном направлении.
, произошел против часовой стрелки, то угол будем считать положительным и говорить, что вращение произошло в положительном направлении.
Наблюдение: Если при изменении аргумента от 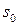 до
до 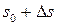 вектор бинормали поворачивается в отрицательном направлении, то векторы
вектор бинормали поворачивается в отрицательном направлении, то векторы 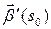 и
и 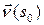 направлены в одно и то же полупространство относительно спрямляющей плоскости. Если вращение положительно – эти векторы направлены в разные полупространства.
направлены в одно и то же полупространство относительно спрямляющей плоскости. Если вращение положительно – эти векторы направлены в разные полупространства.
Определение 8.2. Величину 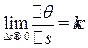 (каппа) (скорость поворота вектора бинормали) будем называть кручением.
(каппа) (скорость поворота вектора бинормали) будем называть кручением.
Вычислительные формулы для кручения.
Как и при подсчете кривизны в натуральном параметре, получаем
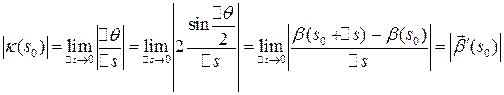
Продифференцируем равенство 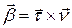 (для удобства аргументы опускаем, хотя в качестве упражнения рекомендуем их восстановить):
(для удобства аргументы опускаем, хотя в качестве упражнения рекомендуем их восстановить):
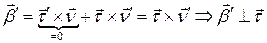
Кроме того 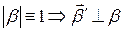 . Значит
. Значит 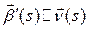 или
или 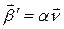 .
.
Переходя к модулям, получаем 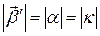 , значит
, значит 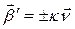 откуда с учетом наблюдения (кручение, как скорость поворота бинормали, будет положительным (отрицательным), если скалярное произведение
откуда с учетом наблюдения (кручение, как скорость поворота бинормали, будет положительным (отрицательным), если скалярное произведение 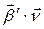 отрицательно (положительно)), получаем
отрицательно (положительно)), получаем
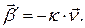
Учитывая, а также то, что 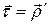 и
и 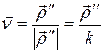 , получаем
, получаем
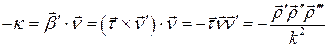 .
.
Таким образом, верна
Теорема 8.1. Пусть 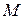 ‑ произвольная точка (ориентированной) кривой
‑ произвольная точка (ориентированной) кривой 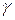 . Тогда кручение
. Тогда кручение 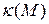 кривой
кривой 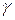 в точке
в точке 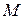 вычисляется по формуле
вычисляется по формуле
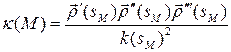 ,
,
где 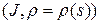 ‑ некоторая (какая-нибудь) н-параметризация некоторой окрестности
‑ некоторая (какая-нибудь) н-параметризация некоторой окрестности  точки
точки 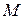 на кривой
на кривой 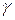 .
.
Упражнение 8.1. Пусть 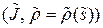 ‑ еще одна н-параметризация окрестности
‑ еще одна н-параметризация окрестности  ,
, 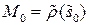 и
и 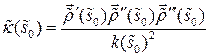 . Тогда
. Тогда 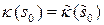 .
.
Вычислительные формулы для кручения в произвольной параметризации.
Пусть 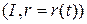 произвольная параметризация окрестности
произвольная параметризация окрестности  и
и 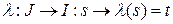 ‑ замена параметра. Тогда из равенства
‑ замена параметра. Тогда из равенства 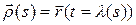 дифференцированием получаем:
дифференцированием получаем:
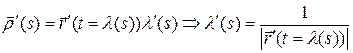
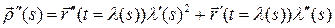
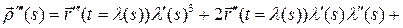
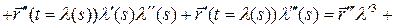 (линейная комбинация векторов
(линейная комбинация векторов 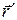
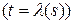 и
и 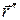
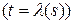 ).
).
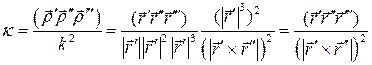 .
.
В итоге получаем:
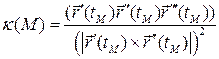
§9. Формулы Френе
Теорема 9.1. Пусть 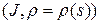 натуральная параметризация окрестности
натуральная параметризация окрестности  на ориентированной кривой
на ориентированной кривой 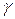 ,
, 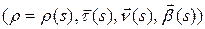 ‑ репер Френе, а
‑ репер Френе, а 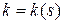 и
и 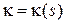 ‑ кривизна и кручение кривой в точке
‑ кривизна и кручение кривой в точке 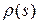 . Тогда имеют место формулы:
. Тогда имеют место формулы:
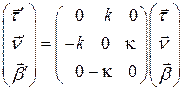
 Заметим сразу, что
Заметим сразу, что 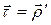 . Кроме того, из леммы о вектор-функции постоянной длины и следует, что
. Кроме того, из леммы о вектор-функции постоянной длины и следует, что 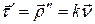 . Дифференцируя равенство
. Дифференцируя равенство 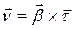 и используя, получаем
и используя, получаем
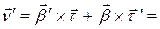
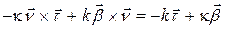 .
. 
Критерии плоской кривой.
Теорема 9.2. Кривая является плоской тогда и только тогда, когда все ее соприкасающиеся плоскости совпадают.
 Пусть
Пусть 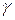 лежит в плоскости
лежит в плоскости 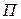 ,
, 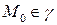 и
и 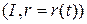 ‑ произвольная параметризация окрестности
‑ произвольная параметризация окрестности  , содержащей точку
, содержащей точку 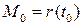 . Так как
. Так как 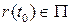 ,
, 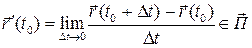 (‑ направляющее пространство плоскости
(‑ направляющее пространство плоскости 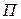 ) и
) и 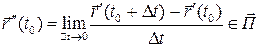 , то соприкасающаяся плоскость кривой в точке
, то соприкасающаяся плоскость кривой в точке 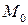 совпадает с плоскостью
совпадает с плоскостью 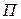 .
.
Наоборот, пусть все соприкасающиеся плоскости совпадают и совпадают с плоскостью 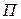 . Для
. Для 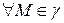 лежит в некоторой соприкасающейся плоскости, которая в свою очередь совпадает с
лежит в некоторой соприкасающейся плоскости, которая в свою очередь совпадает с 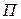 , следовательно
, следовательно 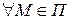 .
. 
Теорема 9.3. Кривая является плоскойтогда и только тогда, когда 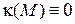 .
.
Пусть 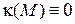 . Сначала докажем, что у каждой точки кривой существует окрестность на кривой, целиком принадлежащая некоторой плоскости. В самом деле, для произвольной точки
. Сначала докажем, что у каждой точки кривой существует окрестность на кривой, целиком принадлежащая некоторой плоскости. В самом деле, для произвольной точки 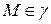 существует окрестность
существует окрестность  , которая может быть параметризована. Предположим, что
, которая может быть параметризована. Предположим, что 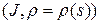 ‑ натуральная параметризация
‑ натуральная параметризация  . По формулам Френе
. По формулам Френе 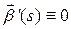 , то есть
, то есть 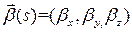 ‑ постоянный вектор. Но тогда
‑ постоянный вектор. Но тогда 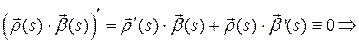
|
|
|
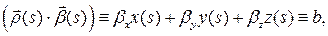
где 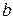 ‑ некоторое постоянное число. Формула говорит о том, что при любом
‑ некоторое постоянное число. Формула говорит о том, что при любом 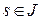 точка
точка 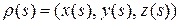 лежит в плоскости
лежит в плоскости
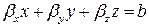
Теперь заметим, что какую бы дугу кривой мы не взяли, ее можно, в силу компактности, покрыть конечным числом параметризованных окрестностей, каждая из которых лежит в плоскости (6), откуда следует, что кривая целиком лежит в этой плоскости.
Наоборот: пусть кривая плоская. Тогда все ее соприкасающиеся плоскости совпадают. Следовательно, выбрав н-параметризацию окрестности произвольной точки 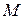 кривой, получим
кривой, получим 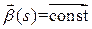 и
и 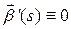 . В силу формул Френе получаем
. В силу формул Френе получаем 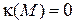

§10. Локальное строение кривой
Пусть 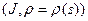 натуральная параметризация окрестности
натуральная параметризация окрестности 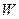 точки
точки 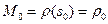 кривой
кривой 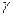 , а
, а 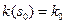 и
и 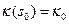 кривизна и кручение в точке
кривизна и кручение в точке 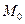 соответственно. Обозначим
соответственно. Обозначим 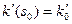 ,
, 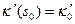 и
и 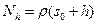 . Если
. Если 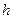 принимает произвольное значение из промежутка
принимает произвольное значение из промежутка 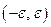 , то
, то 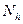 ‑ произвольная точка из некоторой окрестности
‑ произвольная точка из некоторой окрестности 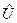 точки
точки 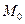 кривой. Считая, что
кривой. Считая, что 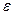 достаточно мало, разложим
достаточно мало, разложим 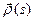 в ряд Тейлора:
в ряд Тейлора:
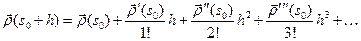
Тогда для радиус-вектора 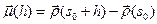 точки
точки 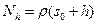 в репере Френе
в репере Френе 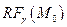 =
= 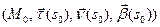 с учетом формул Френе имеем
с учетом формул Френе имеем
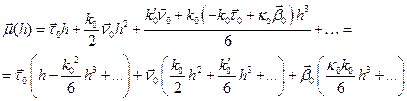
Обозначив 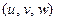 ‑ координаты точки в репере
‑ координаты точки в репере 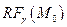 , получим параметрическое уравнение окрестности
, получим параметрическое уравнение окрестности 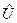 точки
точки 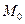 на кривой
на кривой 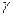 :
:
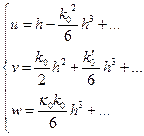
Уравнение позволяет восстановить проекции окрестности 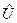 на координатные плоскости репера
на координатные плоскости репера 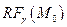 .
.
§11. Существование и единственность кривой
с заданными кривизной и кручением.
Рассмотрим 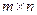 -матрицу
-матрицу 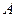 , компонентами которой являются гладкие функции, заданные на интервале
, компонентами которой являются гладкие функции, заданные на интервале 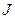 .
.  Пусть
Пусть 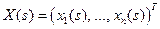 ‑ столбец, компонентами которого являются гладкие функции, определенные на интервале
‑ столбец, компонентами которого являются гладкие функции, определенные на интервале 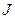 . Тогда, как известно из теории дифференциальных уравнений, система дифференциальных уравнений
. Тогда, как известно из теории дифференциальных уравнений, система дифференциальных уравнений 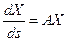 имеет единственное максимальное решение удовлетворяющее заданным начальным условиям
имеет единственное максимальное решение удовлетворяющее заданным начальным условиям 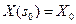 .
.
Теорема 11.1 (об инвариантности репера Френе). Пусть 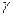 ‑ кривая в
‑ кривая в 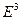 ,
, 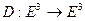 ‑ движение. Тогда
‑ движение. Тогда
i) 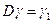 ‑ кривая;
‑ кривая;
ii) если 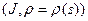 ‑ натуральная параметризация окрестности
‑ натуральная параметризация окрестности 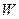 на кривой
на кривой 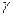 , то
, то 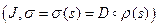 ‑ натуральная параметризация окрестности
‑ натуральная параметризация окрестности 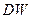 на кривой
на кривой 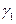 .
.
|
|
|
iii) 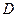 (
(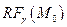 )
) 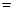
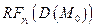 .
.
 Доказательство проведем для случая, когда кривая параметризована глобально, и
Доказательство проведем для случая, когда кривая параметризована глобально, и 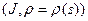 ‑ параметризация
‑ параметризация 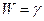 . Рассмотрим пару
. Рассмотрим пару 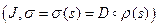 :
:
i)
а). В ортонормированной системе координат движение имеет координатное выражение вида: 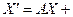
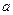 , где
, где 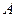 ‑ ортогональная матрица (
‑ ортогональная матрица (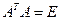 ) и
) и 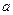 ‑
‑ 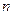 -столбец. Являясь полиномами 1-ой степени, координатные функции координатного выражения движения гладки. Следовательно, движение – гладкое отображение. Теперь ясно, что
-столбец. Являясь полиномами 1-ой степени, координатные функции координатного выражения движения гладки. Следовательно, движение – гладкое отображение. Теперь ясно, что 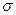 ‑ гладко, так как является композицией гладких отображений.
‑ гладко, так как является композицией гладких отображений.
б). Обозначив 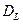 линейную часть движения
линейную часть движения 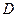 , с учетом, для базиса
, с учетом, для базиса 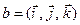 имеем
имеем
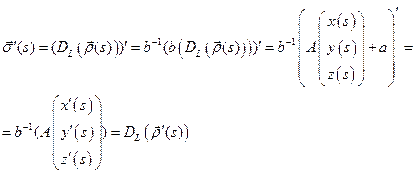
Так как 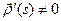 , а
, а 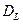 сохраняет длины векторов, то и
сохраняет длины векторов, то и 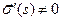 , то есть
, то есть 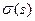 ‑ регулярное отображение.
‑ регулярное отображение.
в). 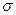 инъективно, как композиция инъективных отображений.
инъективно, как композиция инъективных отображений.
г). Взаимная непрерывность следует из взаимной непрерывности 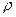 и непрерывности
и непрерывности 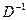 . Таким образом,
. Таким образом, 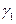 ‑ кривая.
‑ кривая.
ii) Так как линейная часть движения сохраняет длины векторов, то из следует, что 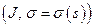 ‑ натуральная параметризация, если только
‑ натуральная параметризация, если только 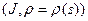 ‑ натуральная.
‑ натуральная.
iii) Пусть 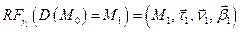 ‑ репер Френе кривой
‑ репер Френе кривой 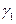 в точке
в точке 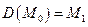 .
.
а). 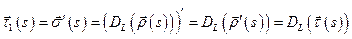 .
.
б).
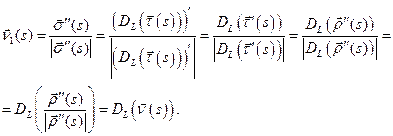
в).
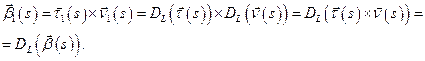
Теорема 11.2 (теорема о единственности кривой).
Пусть 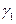 и
и 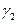 две кривые, а
две кривые, а 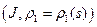 и
и 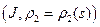 ‑ их глобальные натуральные параметризации. Пусть также в соответствующих точках (в точках, полученных при одном и том же значении параметра) их кривизны и кручения совпадают:
‑ их глобальные натуральные параметризации. Пусть также в соответствующих точках (в точках, полученных при одном и том же значении параметра) их кривизны и кручения совпадают: 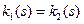 и
и 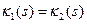 . Тогда существует движение
. Тогда существует движение 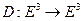 , такое что
, такое что 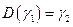 .
.
 Для
Для 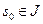 положим
положим 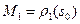
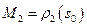 . Существует единственное движение
. Существует единственное движение 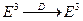 , такое что
, такое что 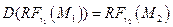 (на векторы репера движение действует своей линейной частью).
(на векторы репера движение действует своей линейной частью).
Пусть 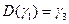 . Кривая
. Кривая 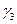 проходит через точку
проходит через точку 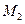 и
и 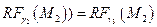 .
.
Обозначив 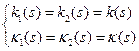 ,
, 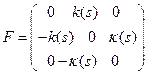 ,
, 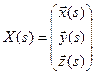 .
.
Система дифференциальных уравнений
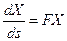
имеет единственное максимальное решение 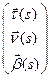 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 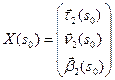 . Но тогда в силу единственности
. Но тогда в силу единственности 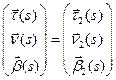 и
и 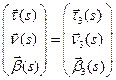 . Таким образом
. Таким образом 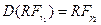 . В частности,
. В частности, 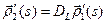 , следовательно
, следовательно 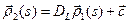 . Так как при
. Так как при 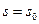
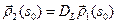 , то
, то 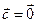 и, значит
и, значит 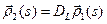 .
. 
Теорема 11.3 (о существовании кривой). Пусть 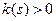 и
и 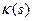 две гладкие функции, заданные на интервале
две гладкие функции, заданные на интервале 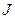 . Тогда существует кривая
. Тогда существует кривая 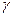 с глобальной натуральной параметризацией
с глобальной натуральной параметризацией 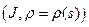 , для которой
, для которой 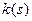 – кривизна, а
– кривизна, а 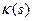 – кручение в точке
– кручение в точке 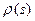 .
.
 Зафиксируем в
Зафиксируем в 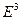 правый ортонормированный репер
правый ортонормированный репер 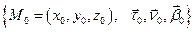 . Для
. Для 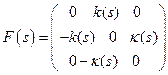 и
и 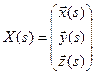 рассмотрим систему дифференциальных уравнений
рассмотрим систему дифференциальных уравнений
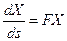
с начальными условиями 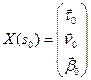 . Эта система имеет единственное максимальное решение
. Эта система имеет единственное максимальное решение 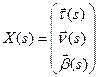 , удовлетворяющее начальным условиям. Покажем, что при любом
, удовлетворяющее начальным условиям. Покажем, что при любом 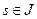 упорядоченная тройка векторов
упорядоченная тройка векторов 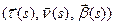 является правым ортонормированным базисом, то есть матрица
является правым ортонормированным базисом, то есть матрица 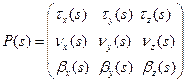 , строки которой состоят из координат соответствующих векторов, ортогональна и
, строки которой состоят из координат соответствующих векторов, ортогональна и 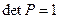 . Сразу заметим, что система эквивалентна системе
. Сразу заметим, что система эквивалентна системе 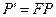 с начальным условием
с начальным условием 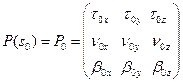 . Так как
. Так как
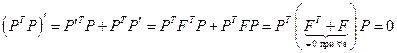 и
и 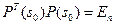 ‑ единичная матрица, то
‑ единичная матрица, то 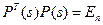 и, в частности,
и, в частности, 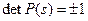 . Из того, что
. Из того, что 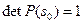 , и непрерывности функции
, и непрерывности функции 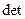 следует
следует 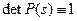 .
.
Осталось лишь показать (это рекомендуется сделать в качестве упражнения), что пара 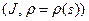 , где
, где 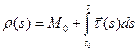 есть н-параметризация кривой
есть н-параметризация кривой 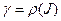 , при этом
, при этом 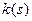 – кривизна, а
– кривизна, а 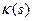 – кручение этой кривой в точке
– кручение этой кривой в точке 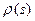 .
. 
 2015-07-14
2015-07-14 1314
1314