Вопросы и задания для самостоятельной работы 11 страница

В начальной школе учащиеся должны получить первые представления об этих зависимостях. И вовсе не потому, что эти зависимости сравнительно просты, а потому что они имеют важное общеобразовательное значение. В самом деле, пропорциональные величины широко представлены в окружающей детей действительности. Это цена, стоимость, количество товара; скорость, расстояние, время движения; выработка в единицу времени (норма выработки), общая выработка, время работы; урожайность, урожай, площадь, с которой он собран; общая масса одинаковых предметов, масса одного из них, количество этих предметов и т. д. Естественно, что с этими величинами учащиеся знакомятся через задачи.

К обучению решению простых задач, раскрывающих связи между пропорциональными величинами, приступают после того, как ученики усвоили смысл операций умножения и деления. Знакомство с названными тройками величин не совпадает по времени. Например, представления о цене и стоимости учащиеся получают гораздо раньше, чем о скорости, урожайности, урожае. действительно, чтобы перейти к рассмотрению понятия «урожайность», необходимо сначала сформировать у учащихся понятие площади, познакомить с мерами массы и площади; чтобы раскрыть смысл понятия скорости, нужно, чтобы ученики знали единицы времени.

Простые задачи с пропорциональными величинами решаются умножением и делением и принадлежат к хорошо известным учащимся типам. Однако, встречаясь с новыми величинами, дети могут испытывать определенные трудности.

Рассмотрим несколько задач на пропорциональность, относящихся к одному типу (задачи, раскрывающие смысл умножения).

З а д а ч а 30. За каждую тетрадь заплатили З к. Купили б таких тетрадей. Сколько стоила покупка?

З а д а ч а 31. Одна табуретка стоит 8 р. Купили 4 такие табуретки. Сколько денег за них уплатили?

З а д а ч а 32. Пионерский отряд находился в пути 3 ч. За каждый час отряд проходил 4 км. Какое расстояние прошли пионеры?

З а д а ч а 33. С каждого гектара колхозного поля собрали по 21 ц пшеницы. Площадь этого поля 5 га. Сколько всего пшеницы собрали?

Учащиеся уже знакомы с краткой записью условий задач данного типа. Поэтому условия задач 30—33 можно записать сначала «традиционно». Например:

Одновременно учитель объясняет, например, что в задаче 30 сказано, что «за каждую тетрадь заплатили З к.», а в задаче 31— что «одна табуретка стоит 8 р.» И в том и в другом случае речь идет о стоимости одного предмета. (<Гораздо короче и грамотнее,— говорит учитель—в таких случаях пользоваться словом «цена»:

цена тетради З к., цена табуретки 8 р.»

Возможно, что, решая задачи, ученики будут испытывать затруднения в выборе необходимого действия. В этих случаях задачи иллюстрируются чертежами (на рис. 62 представлены чертежи к задачам 30, 32, 33). Использование для иллюстраций наборного полотна и предметных множеств нецелесообразно и неэффективно.

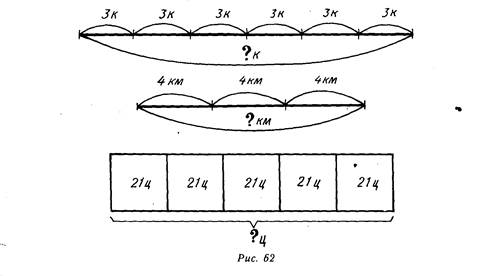
Аналогично организуется работа над задачами с пропорциональными величинами, решаемыми делением. (.— далее у учащихся отрабатывается умение определять цену по

данной стоимости и количеству, стоимость по данной цене и количеству и т. д.; скорость по данному расстоянию и времени, время по данному расстоянию и скорости и т. д. С этой целью полезно использовать, например, такие упражнения:

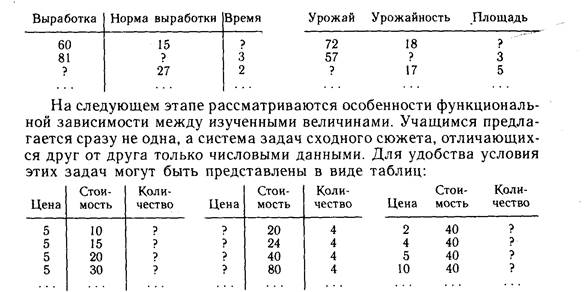
Каждая строка таблицы соответствует отдельной задаче.
Рассмотрим методику работы над такими упражнениями на примере первой таблицы. Сначала выясняются общие особенности задач, представленных в таблице: цена постоянная, стоимость увеличивается, неизвестно количество купленного товара Задачи решаются, и таблица соответствующим образом заполняется.
Анализируются результаты проделанной работы. Числовые значения в третьей колонке возрастают. На вопрос учителя: «Почему?» ученики могут ответить, например, так: «Потому, что стоимость увеличивается». Такой ответ учителя удовлетворить не должен. Поэтому учащимся предлагается еще одна «задача»: Цена 10, стоимость 40; определить количество. Стоимость увеличилась с 30 до 40, а количество тем не менее уменьшилось. Причина этого в изменении цены. Итак, констатируется: если цена постоянна, а стоимость увеличивается, то количество увеличивается тоже.
Наконец, на основании наблюдений, над изменениями значений величин, представленных в таблице, делается более глубокий вывод. Пусть, например, рассматриваются первая, третья и четвертая строки таблицы. Несложно заметить, что стоимость увеличивается соответственно в 2 и З раза. Соответствующие значения количества также увеличиваются, причем в такое же число раз. Такой уровень представлений о пропорциональности для начальной школы вполне достаточен.
По такой же методике и на таком же уровне раскрываются прямая и обратная пропорциональная зависимости и между другими величинами. Эти представления не могут быть, конечно, сформированы в результате однократного выполнения рассмотренных упражнений. Они должны использоваться учителем систематически, допустим, в рамках устного счета. Опыт показывает, что работа над ними не занимает много времени и хорошо сочетается с отработкой вычислительных навыков. -

2. ОБУЧЕНИЕ УЧАЩИХСЯ РЕШЕНИЮ СОСТАВНЫХ ЗАДАЧ
Прежде всего остановимся на проблеме: что значит у м е т ь р е ш а т ь составные задачи. История методики обучения математике свидетельствует, что данная проблема на разных этапах развития науки решалась по-разному.
На рубеже ХIХ и ХХ вв. под умёнием решать задачи понимали способность ученика решать составные задачи вполне определенных типов, так называемые типовые задачи, регламентированные программой. Для этого ученика вооружали четко ограниченным множеством специальных методов (правил) Каждый из них соответствовал задачам определенного типа. Как. свидетельствует 2, И. Шохор-Троцкий, весьма известный в те времена методист, <На гимназических испытаниях зрелости предлагались по предмету арифметики задачи, из которых каждая требовала непременного знания по возможности большего количества приемов решения задач
разного рода* А перечень таких методов был весьма велик:
простое тройное правило и сложное, правила процентов, учета векселей, нахождения средних процентных такс, вычисления сроков платежей, цепное правило, правила пропорционального деления, нахождения неизвестного по двум разностям, вычисления пробы, смещения первого и второго рода, сплавов, замены данных, уравнивания данных и т. д.
Корни такого понимания умения решать составные задачи уходят в далекое прошлое. В учебниках Х1I1-ХiУ вв. число правил, которыми должны были владеть умеющие решать задачи. было огромным что ни задача, то специальное правило. (Заметим, что среди них были правила с довольно экзотическими названиями:
«правило нашедшего кошелька, «правило девиц», правило слепого.)
Такая концепция имела серьезных противников в лице С. И. Шхор-Троцкого, Ф. А. Эрна и др. Однако она продолжала господствовать в методике начального обучения вплоть до середины ХХ в. В советской начальной школе до реформы 1968 г. умение решать задачи отождествлялось с умением решать типовые задачи. Число правил, подлежащих усвоению, было достаточно велико. В их числе уже упоминавшиеся правила смешения и сплавов, тройные правила, правила исключения неизвестного, пропорционального деления и т. д.
В программе 1968 г. количество типовых задач было резко сокращено. Выделялись только два типа задач: решаемых приведением к единице и на пропорциональное деление. Программой 1986 г. обучение школьников решению типовых задач не предусмотрено. Учащиеся «должны постепенно овладевать простейшими общими подходами к решению задач». Такая концепция является весьма серьезным достижением отечественной методики.
Об общих приемах работы над задачей, которыми могут овладеть младшие школьники, подробно говорилось в § 19. Там же были рассмотрены общие вопросы методики формирования этих приемов. Поэтому остановимся на важном следствии из современной концепции обучения решению составных задач: учитель должен проявлять творческую инициативу в разработке системы составных задач; целесообразность этой системы определяется следующим условие обеспечивает ли она усвоение учащимися общих приемов работ над задачей? Творческая активность учителя в этой области имеет большое значение для развития умственных способностей учащихся и подготовки младших школьников к изучению математики в средних и старших классах.
Активная позиция учителя в совершенствовании процесса обучения решению задач должна сообразовываться со следующим требованием.
Учитель может предложить учащимся решить задачу, если видит, что ее содержание допускает интерпретации на всех возможных уровнях: с помощью краткой записи, чертежа, предметной иллюстрации и практической работы (подробно об этом сказано в § 19). Причем каждый уровень интерпретации должен быть доступен пониманию учащихся, согласовываться с их знаниями, умениями и навыками.

Рассмотрим задачу: «Определить наименьшее количество носильщиков, с которыми геолог может совершить шестидневный переход через пустыню, если он сам и каждый из носильщиков могут нести лишь четырехдневный запас еды». Очевидно, что кратко записать условие этой задачи школьники не смогут. Очень сложно проиллюстрировать ее содержание графически, следовательно, эта задача не для начальной школы.

Рассмотрим следующую задачу: «Купили два отреза ткани

один по цене б р., а другой 8 р. за метр. Стоимость обоих отрезов одинакова, но в первом было на 2 м ткани больше, чем во втором. Сколько ткани в одном отрезе и сколько в другом?» (отметим, что эта задача сложнее, чем допускалось программой 1968 г.). В данной задаче рассматриваются пропорциональные величины. Поэтому кратко ее условие, как известно учащимся, записывается в виде таблицы:

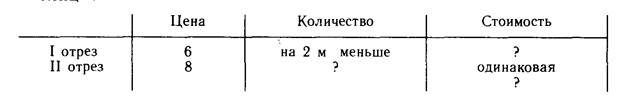
Можно предвидеть, что этого будет недостаточно, чтобы дети самостоятельно решили задачу, поэтому учитель должен иметь альтернативный вариант интерпретации с помощью чертежа. Если не удаётся придумать чертеж, доступный пониманию детей, предлагать эту задачу учащимся нет смысла. В данном случае чертеж достаточно прост (рис. 63). Из рисунка видно, что несложно опреде

лить, какое число соответствует отрезку СВ: 6- 2= 12 на столько меньше заплатили бы за первый отрез, если бы по длине он был равен второму.

Возможно, что, опираясь на чертеж, учащиеся не смогут самостоятельно решить задачу. Теперь все зависит от способности учителя придумать доступную предметную иллюстрацию. В качестве предметов» могут быть использованы модели отрезков, соответствующие цене одного и другого материала. Отрезки укладываются парами (рис. 64). Ученики могут заметить, что всякий раз, когда от А укладывается «шестирублевый» отрезок, а справа — «восьми- рубленый», разница в стоимости покупок увеличивается на 2 р. Если бы длина первого отреза равнялась длине второго, то разница

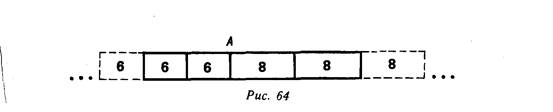
в стоимости отрезов, как уже известно, составила бы 12 р.Чтобы это условие выполнялось, нужно уложить б пар отрезков. Итак, идея решения найдена уже на основе предметной иллюстрации. Однако на всякий случай учителем должен быть продуман вариант еще более наглядного представления содержания задачи.

Из рассмотренного примера видно, что доступность решения задачи во многом зависит от профессиональной подготовки учителя. Учитель, умеющий хорошо решать задачи и изобретательно их иллюстрировать, может на каждом уроке использовать более сложные и интересные задачи, чем предлагаемые в учебнике. А это обеспечит более высокий уровень преподавания математики в целом.

Остановимся на еще одном вопросе, связанным с составными задачами,— методике обучения учащихся решению задач в два действия. Особенности этой методики обусловлены причинами психологического характера. Как известно, учащиеся в течение долгого времени решают простые задачи. При этом поиск решения сводится, фактически, к выбору арифметического действия, которое нужно выполнить над двумя числовыми данными, содержащимися в условии задачи. Предположим, учащимся предложена следующая задача:

(1) «У Сережи З тетради, а у Наташи на 2 тетради больше. Сколько тетрадей у Сережи и Наташи вместе? Впервые сталкиваясь с составной задачей, учащиеся могут решить ее неверно. Причем ошибки в решении будут достаточно характерными: 3+2=5 или

3+5=8.

Причина первой. ошибки состоит в том, что ученик попытался решить задачу нового типа так же, как хорошо ему известные задачи, в которых слова «больше на» и «вместе» обусловливали выбор операции сложения. Ученик может рассуждать так: в условии даны два числа З и 2, сказано, что «больше на», значит, задача решается выражением 3+2 (или сказано «вместе», значит, 3+2).

другая ошибка свидетельствует о том, что ученик понимает идею решения задачи, но у него не хватает знаний для правильной реализации этой идеи: он никогда не записывал решение задачи выражением, содержащим два действия.

Чтобы предупредить эти ошибки, можно воспользоваться разными методическими приемами. Например, учащимся одновременно предлагаются две задачи, связанные общим сюжетом: (2) «У Сережи З тетради, а у Наташи на 2 тетради больше. Сколько тетрадей у Наташи?»; (3) «У Сережи З тетради, а у Наташи 2. Сколько тетрадей у Сережи и Наташи вместе?» Задачи таких типов школьникам знакомы, и, решая их, они не будут испытывать трудностей. Затем из задач (2) и (3) конструируется задача (1). Обсуждаются особенности задач (2) и (3), с одной стороны, и задачи (1) — с другой.

Вопросы и задания для самостоятельной работы
К. 18
1. Каковы функции текстовых задач в начальном обучении математике? Приведите соответствующие примеры.
2. В чем заключается особенность обучения решению задач в начальных классах?

3. Известно, что текстовые задачи учащиеся начальных классов решают по вполне определенному плану. В чем состоит методика отработки у них соответствующих
умений?
К § 20
4. Приведите классификацию простых задач, решаемых в ‘—‚У классах. Обоснуйте ее.
5. Опишите методику обучения учащихся решению простых задач, раскрывающих смысл: а) операций сложения и вычитания; б) умножения и деления; в) отношений «больше», «меньше», «равно».
б. Назовите особенности формирования у учащихся начальных классов понятий доли и дроби.
7. Раскройте методику обучения школьников решению простых задач, связанных с понятиями доли и дроби.
8. Первоначальные представления о функциональной зависимости формируются у учеников через простые задачи. Каким образом это делается?
К § 21
9. Что такое типовые задачи? Какие возможности для обучения учащихся решению составных задач раскрывает современная программа для начальных классов?
10. Объясните, почему для обучения школьников решению задач в два действия требуется специальная методика? В чем состоит ее суть?

23. МЕТОДИКА ИЗУЧЕНИЯ ЧИСЛОВЫХ ВЫРАЖЕНИЙ
Понятие математического выражения (или просто выражения),
изучаемое в начальных классах, имеет важное значение. Так, это
понятие помогает учащимся овладеть вычислительными навыками.

Выясняется, что, решив задачи (2) и (3), фактически решили и задачу (1). Поэтому ее решение записывается так: 3+(3+2).
Возможен и другой подход при введении задач в два действия. Рассматривается задача с недостающим данным: У Сережи З тетради, а у Наташи... тетрадей. Сколько тетрадей у Сережи и Наташи вместе?» Ученики согласятся, конечно, что такую задачу решить нельзя — не сказано, сколько тетрадей у Наташи. Учитель, например, говорит, что он не знает, сколько тетрадей у Наташи, но ему известно, что у нее на 2 тетради больше, чем у Сережи. Поэтому сначала вычисляется, сколько тетрадей у Наташи (3+2), а затем — сколько всего тетрадей у детей: 3+2+3. В заключение формулируется полный текст решенной задачи.

УI. ЭЛЕМЕНТЫ АЛГЕБРЫ В НАЧАЛЬНОИ ШКОЛЕ
22. ОБЩАЯ ХАРАКТЕРИСТИКА АЛГЕБРАИЧЕСКОГО МАТЕРИАЛА В КУРСЕ МАТЕМАТИКИ НАЧАЛЬНОЙ ШКОЛЫ
достаточно долгое время в психологии господствовало мнение (например, П. П. Блонского), что элементы алгебры следует изучать не в начальных, а в старших классах в силу особенностей мышления младшего школьника, неспособности его к образованию абстракций более высокого уровня. В последние годы исследованиями советских психологов (П. Я. Гальперин, В. В. Давыдов, д. Б. Эльконин и др.) и педагогов (А. И. Маркушевич, А. М. Пышкало и др.) было установлено, что познавательные возможности младших школьников при традиционной системе обучения значительно занижались. дети 6—1О лет при определенной организации обучения могут полноценно усвоить содержание некоторых алгебраических понятий. При этом у них раньше, чем обычно, возникают предпосылки к теоретическому
рассуждению (особенно в связи с введением буквенной символики). На основании этого алгебраический материал был включен в программу по математике для начальных классов в 1969 г.
Включение в содержание обучения элементов алгебры, особенно упражнений с функциональным содержанием, позволяет увидеть
динамичность явлений реального мира, взаимную обусловленность и связь величин, а это оказывает большое влияние на формирование мировоззрения учащихся. Изучение алгебраического материала способствует развитию у учащихся таких логических приемов, как анализ и синтез, обобщение и конкретизация, индукция и дедукция.
Введение элементов алгебры.имеет большое значение для совершенствования системы начального математического образования, расширения арсенала математических средств, используемых школьниками при решении задач. Буквенная символика, вводимая в начальных классах, и связанное с ней понятие переменной способствуют обобщению знаний о числах, свойствах арифметических действий. Таким образом проводится работа по функциональной пропедевтике одного из важнейших понятий современной математики понятия соответствия. Использование уравнений для решения задач позволяет существенно изменить всю систему обучения решению задач.
В целом же алгебраический материал в курсе математики начальной школы выполняет вспомогательную функцию при изучении основного (арифметического) содержания программы.

действительно, часто вычислительные ошибки связаны с непониманием структуры выражений, нетвердым знанием порядка выполнения действий в выражениях. Усвоение понятия выражения обусловливает формирование таких важных математических понятий, как равенство, неравенство, уравнение. Умение составлять выражение по задаче необходимо для овладения умением решать задачи алгебраическим способом, т. е. с помощью составления уравнений.
‚С первыми выражениями — суммой и разностью — дети знакомятся при I4зучении сложения и вычитания в концентре «десяток». Не используя специальных терминов, первоклассники производят вычисления, записывают выражения, читают их, заменяют число суммой, основываясь на наглядных представлениях. При этом выражение 4+3 они читают следующим образом: «к четырем прибавить три» или «4 увеличить на 3», а выражение 4 — З - «из четырех вычесть три» или «4 уменьшить на 3». Находя значения выражений, состоящих из трех чисел, которые соединены знаками сложения и вычитания, учащиеся фактически пользуются правилом порядка выполнения действий в неявном виде и выполняют первые тождественные преобразования выражений.
Познакомившись с выражениями вида а+Ь, первоклассники сначала употребляют термин «сумма» для обозначения числа, получающегося в результате сложения, т. е. сумма трактуется как значение выражения. Затем с появлением более сложных выражений, например вида (а + Ь) с, появляется необходимость иного понимания термина «сумма». Выражение а+Ь называется суммой, а его компоненты — слагаемыми. При введении выражений вида а — Ь, а• Ь, а:Ь поступают аналогично. Сначала разностью произведением, частным) называют значение выражения, а затем само выражение. Одновременно учащимся сообщают названия его компонентов: уменьшаемое, вычитаемое, множители, делимое и делитель. Например, в равенстве 9 — 4 = 5 9 — уменьшаемое, 4 — вычитаемое, 5 — разность. Запись 9 4 также называется разностью. Можно вводить эти термины в другой последовательности: предложить учащимся записать пример 9 — 4, пояснив, что записана разность, и вычислить, чему равна записанная разность. Учитель вводит название полученного числа: 5 — тоже разность. другие числа при вычитании называются: 9 — уменьшаемое, 4 — вычитаемое.
Запоминанию новых терминов способствуют плакаты вида

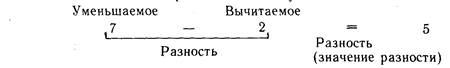
для закрепления этих терминов предлагаются упражнения вида:
Вычислите сумму чисел; запишите сумму чисел; сравните суммы чисел (вставьте знак, или= вместо * в запись 4+3 * 5+ 1 и прочтите полученную запись); замените число суммой одинаковых (разных) чисел; заполните таблицу; составьте по таблице примеры и решите их». Важно, чтобы эти поняли, что при вычислении
суммы производится указанное действие (сложение), а при записи суммы получаем два числа, соединенных знаком плюс.
‘ На следующем этапе усвоения понятия выражения учащиеся знакомятся с выражениями, в которых используются скобки: (10 —
—3)+4, (6—2)+5. Они могут быть введены средством текстов ч. (Соответствующая методика была описаний возможен и другой подход. Учитель предлагает составить на наборном полотне сумму и разность чисел 10 и 3, используя карточки, на которых записаны эти числа и знаки действий. Затем составленную учениками разность 10—3 учитель заменяет подготовленной заранее карточкой с этой разностью. Следующее задание: составить выражение (на этом этапе обучения о нем говорят как о примере), используя разность, число 4 и знак +. При чтении полученного выражения обращается внимание на то, что его компонентами являются разность и число. «Чтобы было заметно,— говорит учитель,— что разность является слагаемым, ее заключают в скобки».
Самостоятельно конструируя выражения, дети осознают их структуру, овладевают умением читать, записывать, вычислять их значения.
Вводятся термины «математическое выражение» (или просто «выражение») и «значение выражения». Определения этих терминов не даются. Записав несколько простейших выражений: сумм, разностей, учитель называет их математическими выражениями. Предложив вычислить эти примеры, он объявляет, что числа, полученные в результате вычисления, называются значением выражения.
дальнейшая работа над числовыми выражениями состоит в том, что дети упражняются в чтении, записи под диктовку, совпадении вычислений, а таблиц, широко используя при этом новые термины.
Затем изучается порядок выполнения действий. Выражения вида:
37—24+3, 63:9. 4 знакомы учащимся: они их читали, записывали под диктовку, вычисляли их значения, еще не зная правил порядка выполнения действий, но уже неявно их используя.
С выражениями вида а + Ь. с, а— Ь. с учащиеся встречаются впервые. В этом случае может быть создана проблемная ситуация. Учащимся предлагается вычислить значение вьг5Т7 Получив различные значения этого выражения, учащиеся сталкиваются с проблемой: какое же из них считать верным. Разрешая ее, учитель формулирует правило порядка выполнения действий в таких выражениях. Важно подчеркнуть, что при выполнении действий в таких выражениях условились выполнять вначале умножение и деление, а затем сложение и вычитание. Это упрощает запись
выражений: произведение и частное записываются без скобок. Чтобы ученики осознанию усвоили правила порядка выполнения действий,
наряду с тренировочными упражнениями на нахождение значения выражения полезны специальные задания: «Вычислите с пояснениями (45—3О):5 и 45—30:5; 15. 3—.28:7; расставьте скобки так, чтобы значение выражения равнялось 105».
Необходимо сформировать у учащихся еще одно практическое умение читать составные выражения. Вначале, выполняя конкретные операции над множествами, ученики осознают смысл сложения и вычитания как «прибавить» и <вычесть», поэтому выражения они читают следующим образом: «к семи прибавить два», «из пяти вычесть один». В дальнейшем понимание действий сложения и вычитания углубляется. Выражения 7+2, 6— 1 читаются следующим образом: «7 увеличить на 2», «уменьшить на 1». С введением названий компонентов действий эти выражения читаются по-другому:
«сумма чисел 7 и 2», «разность чисел б и 1».
Затем учащиеся учатся читать составные выражения, в которых действия выполняются в том порядке, в котором они записаны. Так, выражение 4+2+ 1 учащиеся читают: «к четырем прибавить два и к полученному числу прибавить один», а выражение 24:3• 2 «двадцать четыре разделить на три и полученный результат умножить на два». Для чтения сложных выражений учащиеся используют следующий алгоритм: 1) определяют, какое действие в выражении выполняется последним; 2) вспоминают названия компонентов этого действия; 3) называют, чем выражены его компоненты. Для обучения чтению выражений используется методика работы«по образцу». Например, учитель показывает, как читается выражение 3+7: это сумма, в которой первое слагаемое 3, а второе слагаемое — 7. При чтении сложного выражения 16. 4+10 учитель рассуждает так: «В выражении 16. 4+10 последним выполняется действие сложения, значит, это выражение сумма; компоненты этого действия -слагаемые; первое слагаемое выражено произведением, в котором сомножители — числа 16 и 4, а второе слагаемое
число 10». (Здесь алгоритм использовался два раза.)
Формирование понятия числового выражения тесно связано с обучением учащихся
Поясним это на конкретном. примере. Учащимся предлагается условие задачи: «В магазин привезли З ящика помидоров по 10 кг в каждом и б ящиков огурцов по 15 кг в каждом». Условие задачи содержит 4 числовых данных. Вначале ученики выбирают произвольные пары значений и записывают следующие простые выражения, которые можно объяснить исходя из условия задачи: 3+6 —— общее количество ящиков, привезенных в магазин; 10. 3 масса всех помидоров; 15. 6 — масса всех огурцов; б З — на столько больше привезли ящиков огурцов, чем помидоров; 6:3 — во столько раз больше привезли ящиков огурцов, чем помидоров; 15 10 — на столько больше масса одного ящика огурцов, чем ящика помидоров. Затем учитель предлагает учащимся записать сложные выражения, содержащие два и более действий, опираясь на определенные выражения. Выражение 6. 15 —3. 10 соответствует истинному условию и позволяет ответить на вопрос: «На сколько больше привезли в магазин огурцов, чем помидоров? Выражение 15. 6+10. 3 соответствует вопросу: «Сколько всего овощей привезли в магазин?»
Составление выражений по условию задачи должно вестись цЦьно с составлением задач по выражению.)
С этой целью учащиеся выполняют ряд заданий.

1. у Тани б карандашей, а у Оли 5. Какой вопрос надо поставить к условию задачи, чтобы она решалась так: б -5.
2. В первый день турист прошел 20 км, во второй день — 14 км. Сколько километров он прошел за два дня? Составьте похожую задачу, которая решается так: 18+ [1.
3. Составьте задачу, в которой надо узнать, во сколько раз 15 меньше 45.
4. Составьте задачу по выражению 18:3.
Заметим, что по выражению 18:3 может быть составлена задача на кратное сравнение, на деление по содержанию, на деление на равные части, на нахождение неизвестного множителя.
В такой же последовательности проводится работа и со сложными выражениями (составными задачами): 1) поставьте вопрос к усло- нию задачи, чтобы она решалась данным выражением; 2) составьте задачу по выражению, аналогичную только что решенной; 3) составьте задачу данного вида; 4) составьте задачу по выражению.
24. ФОРМИРОВАНИЕ ПОНЯТИЯ ПЕРЕМЕННОЙ
Введение буквенной символики, осуществляемое в начальном курсе математики, позволяет познакомить учащихся с основными понятиями современной математики: переменной, урав1ением, неравенством и способствует развитию функционального мышления, так как с понятием переменной тесно связана идея функциональной зависимости.
Впервые с упражнениями, раскрывающими понятие переменной, ученики встречаются в первом классе, когда вводятся задания с «окошечками» (пропусками). Окошечко не случайно используется для раскрытия понятия переменной, так как в современной трактовке 1 оно обозначает знак, играющий роль «местодержателя» для имен определенного заданного множества (область значений переменной) -—- множества целых неотрицательных чисел в начальном курсе математики.
В учебнике математики для первого класса встречаются записи вида3+О=5;О+О6;5П0О,заданияпокоторьтм могут быть сформулированы в разной теме, например: «Какое из чисел нужно записать в окошечко, чтобы получилась верная
запись? Восстанови в записи пропущенное число». Вначале при выполнении таких упражнений используются наглядные пособия. Затем, по мере накопления знаний, учащиеся отказываются от них.
Так, при нахождении числа, которое надо вставить в «окошечко» в
‘. записи З + О = 5, предлагается попробовать подставить в «окошечко поочередно числа от О до 4. Вначале такая работа проводится на наборном полотне. Подставляя в «окошечко» карточки с соответствующими числами, ученики выясняют, верна или неверна запись, либо с помощью наглядных пособий, либо опираясь на знание таблиц сложения. Затем примеры такого типа решаются с устным разбором.
Раскрытию понятия переменной способствует и работа по заполнению таблиц:

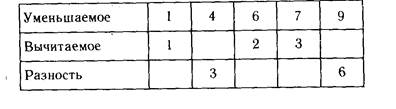
Такие упражнения способствуют не только совершенствованию вычислительных навыков, но и выработке представления о переменной и множестве ее значений. После заполнения таблицы учащимся можно предложить следующие вопросы: какие значения принимает уменьшаемое; вычитаемое; разность? изменяется ли уменьшаемое; вычитаемое; разность? как они изменяются? В некоторых таблицах значения одного из компонентов могут быть постоянными. Таким образом, дети видят, что переменная может принимать не только различные, но и одинаковые значения.
Переменная присутствует и в записях вида О + 1, с которыми первоклассники встречаются при изучении различных случаев сложения и вычитания. Следует обратить внимание детей на эти записи и
объяснить, что в <окошечко> можно подставлять любое из изученных чисел. Так, при изучении прибавления двух может использоваться запись 0+1+1.
Непосредственно перед введением буквенной символики полезно рассмотреть простые арифметические задачи с пропущенными числовыми данными. Подбирая числа, учащиеся получают арифметические задачи, решение которых записывают в виде таблицы (последняя строка таблицы — выражение, являющееся решением задачи).
Второй этап формирования понятия переменной — введение букв как символов для обозначения переменной. На этом этапе широко
используется сочетание индуктивного и дедуктивного методов, осуществляющее переход от числового выражения к буквенному и от буквенного к числовому, учащиеся тем самым обобщают смысл числовых
выражений и конкретизируют его, подставляя вместо букв числовые
значения.
Для раскрытия смысла букв как символов для обозначения
переменной можно использовать однотипные числовые выражения
(суммы) и простые односюжетные арифметические задачи. В последнем случае необходимо акцентировать внимание учащихся не на
ответе, а на выражениях, соответствующих данным задачи: компонент могут быть различными, но их всегда два, и выражение
записывается в виде суммы.
На этом этапе учащиеся выполняют разные по форме и содержанию задания.
1. Найти числовые значения буквенных выражений при заданны значениях букв (задание представлено в виде таблицы).
2. Подобрать числовые значения букв, входящих в выражение,
значение которого задано.
3. Решить простую задачу с буквенными данными. (Работа
над этими задачами осуществляется в такой последовательности:
а) в условие подставляются конкретные числовые значения; б) решение этих задач являются числовые выражения; в) буквенные
выражения выступают как обобщенная запись решения всех задач
с числовыми данными определенного вида.)
Аналогично вводится запись разности двух чисел. Однако в этом
случае дети учатся устанавливать, какие числовые значения могут

принимать буквы, входящие в разность, что фактически является установлением области допустимых значений переменных.
На последнем этапе буквенная символика выступает как средство обобщения знаний учащихся о свойствах действий, взаимосвязям компонентов действий. Обобщение происходит на основе неполной индукции. Учащиеся знакомятся с некоторым множеством однородных выражений. С помощью анализа, сравнения, синтеза они устанавливают общие и существенные свойства этих выражений, т. е. приходят к обобщенным теоретическим знаниям. Поэтому использование буквенной символики как средства обобщения формируемых знаний может осуществляться только тогда, когда учащиеся многократно наблюдали обобщаемые свойства, зависимость, формулировали их и использовали при выполнении различных упражнений. Ученики приходят к пониманию, что использование буквенной символики для записи определенных зависимостей, свойств, отношений означает, что изучаемые зависимости справедливы для любых значений переменных. С этой целью следует предусмотреть’ упражнения, выполняя которые учащиеся овладевают умениями записывать с помощью букв свойства арифметических действий, взаимосвязи компонентов действий, читать свойства и зависимости, записанные с помощью буквенной символики, выполнять тождественные преобразования выражений с переменными на основе знания свойств действий, смысла арифметических действий, доказывать справедливость равенства или неравенства, опираясь на знание элементов теории.
Приведем примеры таких упражнений. Для усвоения переместительного свойства умножения можно предложить следующие задания:
1) сравните выражения: 15. 20 и 20. 15, 40. 11 и 11. 40;
2) замените буквы числами так, чтобы получились верные равенства: 23 а=а• 23. При выполнении этого задания учитывается, что одна и та же буква принимает в равенстве одно и то же значение;
3) чему равно произведение 124. 362, если 362 124=44 888? Найдите значение выражения с• т, если т с = 96 (т и с в обоих равенствах одинаковы);
4) закончите запись т. п = п•
С целью формирования у учащихся умения доказывать справедливость полученных равенств или неравенств выполняются специальные упражнения. Например, требуется проверить равенство(а Ь) Х Х с=а. с— Ь с или сравнить выражения а:(Ь с)=а:Ь:с.
Во всех этих случаях, после того как проведено доказательство, основанное на знании учащимися элементов теории, полезно предложить им убедиться в справедливости равенства или неравенства, придан буквам различные числовые значения. Лучше, если каждый ученик выберет произвольные числовые значения, тогда при проверке можно показать, что вывод, сделанный на основе применения общего правила, верен при любых значениях букв.