Предварительно введем ряд понятий и докажем ряд утверждений.
Определение. Разрезом 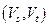 в сети
в сети 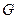 называется пара множеств
называется пара множеств 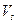 и
и 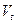 , удовлетворяющих условиям:
, удовлетворяющих условиям:
1. 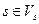 ,
, 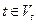 ;
;
2. 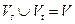 ;
;
3. 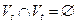 .
.
Через 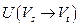 обозначим множество всех дуг, начала которых лежат в
обозначим множество всех дуг, начала которых лежат в 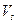 , а концы – в
, а концы – в 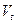 , а через
, а через 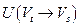 - множество всех дуг, начала которых лежат в
- множество всех дуг, начала которых лежат в 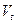 , а концы – в
, а концы – в 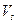 .
.
Определение. Положим 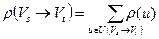 . Число
. Число 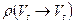 называется пропускной способность разреза
называется пропускной способность разреза 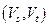 .
.
Также для разреза 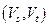 введем числовые характеристики:
введем числовые характеристики:
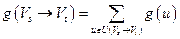 ,
,
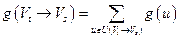 .
.
Пример 4. Для сети и потока 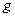 в ней из примера 1, рассмотрим разрез
в ней из примера 1, рассмотрим разрез 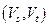 , где
, где 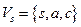 и
и 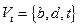 . Имеем:
. Имеем: 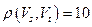 ,
, 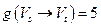 ,
, 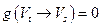 .
.
Лемма 1. Для любого потока 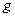 и любого разреза
и любого разреза 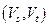 справедливо равенство
справедливо равенство 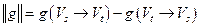 .
.
Доказательство. Согласно условию сохранения потока в вершинах для произвольной вершины 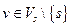 имеем:
имеем: 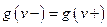 , или
, или 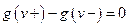 . Следовательно,
. Следовательно,
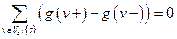 . (1)
. (1)
Кроме того
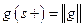 . (2)
. (2)
Сложив почленно равенства (1) и (2), получим
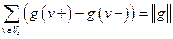 ,
,
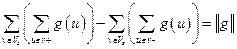 ,
,
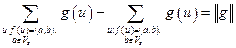 ,
,
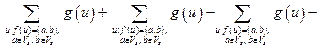
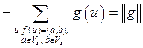 .
.
Первое и третье слагаемые последнего равенства взаимно уничтожаются, следовательно,
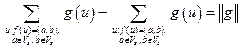 ,
,
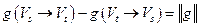 . ■
. ■
Следствие 1. 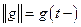 .
.
Доказательство. Пусть 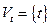 ,
, 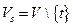 . Тогда
. Тогда 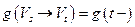 ,
, 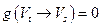 и равенство из леммы 1 запишется следующим образом:
и равенство из леммы 1 запишется следующим образом: 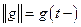 . ■
. ■
Следствие 2. Для любого потока 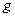 и любого разреза
и любого разреза 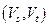 справедливо неравенство
справедливо неравенство 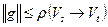 .
.
|
|
|
Доказательство. Из условия ограничения по пропускной способности 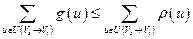 , т.е.
, т.е.
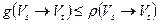 .
.
Тогда с учетом равенства из леммы 1 имеем:
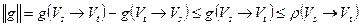 ■
■
Определение. Разрез 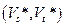 называется минимальным, если для любого разреза
называется минимальным, если для любого разреза 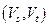 справедливо неравенство
справедливо неравенство
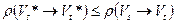 .
.
Лемма 2. Если для некоторого потока 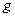 и некоторого разреза
и некоторого разреза 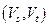 выполняется равенство
выполняется равенство 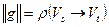 , то поток
, то поток 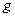 максимален, а разрез
максимален, а разрез 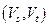 минимален.
минимален.
Доказательство. Пусть 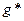 - максимальный поток, а
- максимальный поток, а 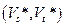 - минимальный разрез. Тогда справедлива следующая цепочка неравенств
- минимальный разрез. Тогда справедлива следующая цепочка неравенств
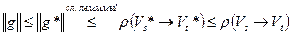 .
.
Поскольку крайние члены в этой цепочке неравенств совпадают, то она превращается в цепочку равенств, что означает, что поток 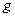 максимален, а разрез
максимален, а разрез 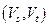 минимален. ■
минимален. ■
Лемма 3. Пусть 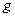 - поток в сети
- поток в сети 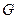 и
и 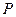 –
– 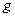 -дополняющая цепь из
-дополняющая цепь из 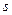 в
в 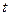 . Тогда в сети
. Тогда в сети 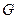 существует поток
существует поток 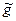 такой, что
такой, что
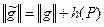 .
.
Доказательство. Определим в сети 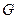 функцию
функцию 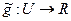 по формуле
по формуле
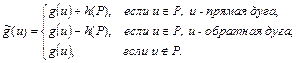
Докажем, что функция 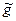 является потоком.
является потоком.
Вначале покажем, что функция 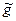 неотрицательна и удовлетворяет условию 1) определения потока.
неотрицательна и удовлетворяет условию 1) определения потока.
Пусть 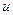 - прямая дуга цепи
- прямая дуга цепи 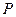 . Тогда
. Тогда
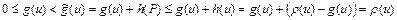 .
.
Пусть 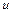 - обратная дуга цепи
- обратная дуга цепи  . Тогда
. Тогда
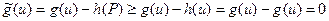
и
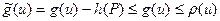 .
.
Таким образом, для любой дуги 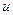 цепи
цепи 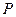 выполнено
выполнено 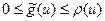 . Если
. Если 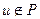 , то
, то 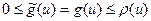 .
.
Теперь убедимся в выполнении для функции 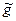 условия 2) определения потока. Понятно, что это условие следует проверить лишь для вершин
условия 2) определения потока. Понятно, что это условие следует проверить лишь для вершин 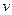 , входящих в цепь
, входящих в цепь 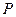 . Пусть
. Пусть 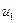 - дуга, по которой «пришли» в вершину
- дуга, по которой «пришли» в вершину 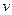 , а
, а 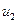 - дуга, по которой «ушли» из
- дуга, по которой «ушли» из 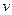 . Каждая из этих дуг может быть как прямой, так и обратной в цепи
. Каждая из этих дуг может быть как прямой, так и обратной в цепи 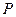 . Следовательно, возможны четыре различных случая.
. Следовательно, возможны четыре различных случая.
1. Пусть обе дуги 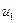 и
и 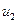 прямые. В этом случае,
прямые. В этом случае,
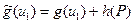 и
и 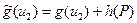 ,
,
так что
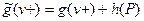 и
и 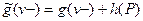 .
.
Но для потока 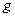 выполнено условие
выполнено условие 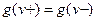 , следовательно, и для потока
, следовательно, и для потока 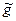 имеем
имеем 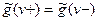 .
.
|
|
|
2. Пусть дуга 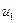 - прямая и
- прямая и 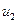 - обратная, т.е. обе дуги входят в вершину
- обратная, т.е. обе дуги входят в вершину 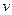 . В этом случае,
. В этом случае,
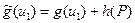 и
и 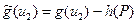 ,
,
так что
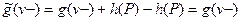 и
и 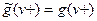 .
.
Так как для потока 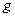 выполнено условие
выполнено условие 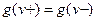 , то и для потока
, то и для потока 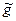 имеем
имеем 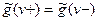 .
.
Аналогично рассматриваются случай 3 (обе дуги 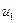 и
и 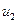 - обратные) и случай 4 (дуга
- обратные) и случай 4 (дуга 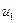 - обратная и
- обратная и 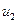 - прямая).
- прямая).
Таким образом, мы показали, что функция 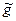 - поток в цепи
- поток в цепи 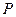 .
.
Определим теперь величину потока 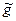 . Напомним, что
. Напомним, что 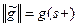 . Из вершины
. Из вершины 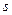 дуги только выходят, поэтому та единственная дуга
дуги только выходят, поэтому та единственная дуга 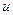 с началом в вершине
с началом в вершине 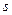 , которая входит в цепь
, которая входит в цепь 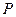 , является прямой дугой цепи
, является прямой дугой цепи 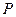 . Следовательно, для нее выполнено равенство
. Следовательно, для нее выполнено равенство 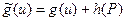 . На остальных дугах, выходящих из
. На остальных дугах, выходящих из  , поток не менялся, так что имеем:
, поток не менялся, так что имеем:
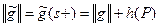 . ■
. ■
Объединяет приведенные выше результаты следующая теорема.
Теорема (Форд, Флакерсон). Для потока 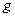 в сети
в сети 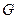 следующие условия эквивалентны:
следующие условия эквивалентны:
1. поток 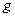 максимален;
максимален;
2. не существует 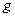 - дополняющей цепи из
- дополняющей цепи из 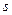 в
в 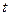 ;
;
3. существует разрез 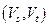 , для которого
, для которого 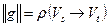 .
.
Доказательство. Доказательство проведем по следующей схеме: 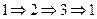 .
.
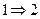 . Будем рассуждать от противного. Предположим, что для максимального потока
. Будем рассуждать от противного. Предположим, что для максимального потока 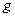 найдется
найдется 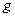 -дополняющая цепь
-дополняющая цепь 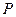 из
из 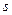 в
в 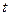 . Тогда по лемме 3 существует поток
. Тогда по лемме 3 существует поток 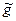 такой, что
такой, что 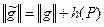 , т.е.
, т.е. 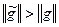 . Полученное неравенство противоречит тому, что поток
. Полученное неравенство противоречит тому, что поток 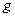 максимален.
максимален.
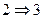 . Определим
. Определим 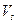 как множество всех вершин
как множество всех вершин 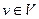 , для каждой из которых существует
, для каждой из которых существует 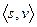 -цепь
-цепь 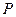 такая, что
такая, что 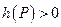 . Добавим в
. Добавим в 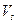 вершину
вершину 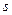 и положим
и положим 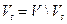 . Докажем, что для полученного разреза
. Докажем, что для полученного разреза 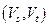 выполняется равенство
выполняется равенство 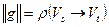 .
.
Покажем, что для любой дуги 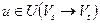 выполнено равенство
выполнено равенство 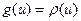 . Будем рассуждать от противного. Предположим, найдется дуга
. Будем рассуждать от противного. Предположим, найдется дуга 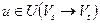 , для которой
, для которой 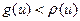 . Пусть
. Пусть 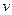 - начало,
- начало, 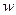 - конец этой дуги,
- конец этой дуги, 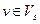 ,
, 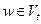 . Множество
. Множество 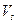 определено нами так, что можно говорить о существовании
определено нами так, что можно говорить о существовании 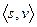 -цепи
-цепи 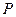 , для которой
, для которой 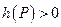 . Дополним эту цепь дугой
. Дополним эту цепь дугой 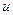 и вершиной
и вершиной 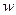 до
до 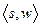 -цепи
-цепи 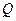 . Будем иметь:
. Будем иметь: 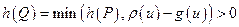 (здесь учтено, что
(здесь учтено, что 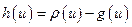 , поскольку
, поскольку 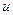 - прямая дуга в цепи
- прямая дуга в цепи 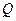 ). Но выполнение неравенства
). Но выполнение неравенства 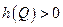 означает, что вершина
означает, что вершина 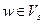 . Пришли к противоречию. Таким образом, предположение было неверным и для любой дуги
. Пришли к противоречию. Таким образом, предположение было неверным и для любой дуги 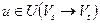 выполнено равенство
выполнено равенство 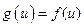 . Следовательно,
. Следовательно, 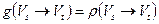 .
.
Аналогично показывается, что для всех дуг 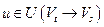 имеет место равенство
имеет место равенство 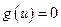 и, следовательно,
и, следовательно, 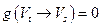 . Поскольку (в силу леммы 1) для любого разреза справедливо равенство
. Поскольку (в силу леммы 1) для любого разреза справедливо равенство 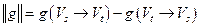 , для построенного разреза получаем равенство
, для построенного разреза получаем равенство 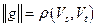 .
.
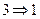 . Это утверждение полностью совпадает с утверждением доказанной ранее леммы 2. ■
. Это утверждение полностью совпадает с утверждением доказанной ранее леммы 2. ■
Следствие. Величина максимального потока в произвольной сети равна пропускной способности минимального разреза.
Замечание. В ходе доказательства теоремы при обосновании справедливости перехода 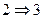 был, по существу, предложен алгоритм нахождения минимального разреза. А именно: пусть найден максимальный поток
был, по существу, предложен алгоритм нахождения минимального разреза. А именно: пусть найден максимальный поток 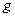 ; находим
; находим 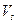 как множество всех вершин
как множество всех вершин 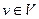 , для каждой из которых существует
, для каждой из которых существует 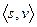 -цепь
-цепь 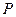 такая, что
такая, что 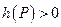 ; добавляем в
; добавляем в 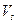 вершину
вершину 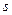 и положим
и положим 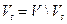 . Полученный
. Полученный 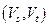 разрез минимален.
разрез минимален.
Пример 5. Для сети из примера 1, разрез 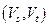 , где
, где 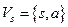 и
и 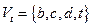 , минимален.
, минимален.
 2015-07-14
2015-07-14 789
789