Федеральное агентство железнодорожного транспорта
Государственное образовательное учреждение
Высшего профессионального образования
Российская открытая академия транспорта
Московского государственного университета путей сообщения
Факультет: «Экономический»
Курсовой проект по дисциплине:
«Финансовая среда предпринимательства и
Студентки 5-6 курса з/о
Бобыр Т.А.
1010-п/ФК-8011
Проверила: ст.преп.Сертакова Е.Н.
Москва 2014г.
Содержание
Задача 1………………………………………………………………………….…3
Задача 2…………………………………………………………...……………......9
Задача 3 …………………………………………….…………………………….16
Задача 4…………………………………………………………………………...33
Список литературы………………………………………………………………21
ЗАДАНИЕ 1. Выбор варианта вложения капитала на основе оценки риска инвестиционных проектов.
Выберите вариант вложения капитала (А или Б). Сравнение вариантов для выбора наиболее выгодного проведите по:
а) получаемой наибольшей сумме средней прибыли с учетом рискованности хозяйственных ситуаций;
б) наименьшей колеблемости прибыли;
в) относительному коэффициенту, учитывающему значения среднего ожидаемого финансового результата и среднего квадратичного отклонения.
Полученные результаты сравните и сделайте вывод о выгодности вложения капитала.
Исходные данные приведены в таблице 1 (для варианта А) и таблице 2 (для варианта Б).
Вариант вложения капитала А тыс. руб. (вариант № 1)
Таблица 1
| Число случаев наблюдения | Полученная прибыль/убыток |
Вариант вложения капитала Б тыс. руб. (вариант № 1)
Таблица 2
| Число случаев наблюдения | Полученная прибыль/убыток |
Решение.
Математический аппарат для количественной оценки риска базируется на методах теории вероятности и математической статистики. В идеальном случае для определения точной вели чины риска необходимо знать все возможные исходы какого-либо события и вероятности этих исходов. Однако на практике, как правило, невозможно получить все значения конечного финансового результата того или иного вида деятельности. Поэтому для количественной оценки риска используют имеющиеся статистические данные, которые позволяют рассчитать уровень риска с достаточно высокой степенью точности.
Величина риска вложения капитала может быть характеризована двумя критериями:
1. Среднее ожидаемое значение прибыли (убытка);
2. Колеблемость (изменчивость) возможного результата.
Среднее ожидаемое значение прибыли (убытка) является средневзвешенным для всевозможных результатов, где в качестве вероятности каждого результата используется его частота, полученная по статистической выборке, и определяется по формуле
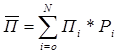 ,
,
где П 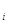 - возможный вариант полученного финансового результата (размер прибыли или убытка);
- возможный вариант полученного финансового результата (размер прибыли или убытка);
Р 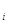 - вероятность (частота) получения одного и того же i – го финансового результата;
- вероятность (частота) получения одного и того же i – го финансового результата;
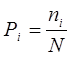 ,
,
где n 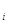 - количество случаев получения одного и того же i – го финансового результата;
- количество случаев получения одного и того же i – го финансового результата;
N – объем выборки, состоящей из всех рассматриваемых случаев.
Таблица 3
| Номер наблюдения | Получ.прибыль, тыс. руб. | Число случаев наблюдения | Расчет | ||||
| Рi | 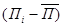 | 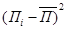 | 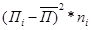 | ||||
| Вариант вложения капитала А | |||||||
| 0,09 | 37,4 | 1398,76 | 39165,28 | ||||
| 0,02 | 166,4 | 27688,96 | 166133,76 | ||||
| 0,04 | -7,6 | 57,76 | 635,36 | ||||
| 0,14 | -17,6 | 309,76 | 13319,68 | ||||
| 0,09 | -20,6 | 424,36 | 11457,72 | ||||
| 0,12 | 12,4 | 153,76 | 5842,88 | ||||
| 0,13 | 23,4 | 547,56 | 21354,84 | ||||
| 0,14 | 6,4 | 40,96 | 1843,20 | ||||
| 0,07 | 63,4 | 4019,56 | 92499,88 | ||||
| 0,01 | -119,6 | 14304,16 | 42912,48 | ||||
| 0,05 | -75,6 | 5715,36 | 97161,12 | ||||
| 0,10 | -69,6 | 4844,16 | 150168,96 | ||||
| Итого | 137,6 | - | - | Σ = 642455,16 | |||
| Вариант вложения капитала Б | |||||||
| 0,10 | -19,89 | 395,61 | 2769,27 | ||||
| 0,16 | -13,89 | 252,49 | 2777,39 | ||||
| 0,21 | -1,89 | 3,57 | 53,55 | ||||
| 0,09 | 10,11 | 102,21 | 613,26 | ||||
| 0,06 | 32,11 | 1031,05 | 4124,20 | ||||
| 0,11 | 0,11 | 0,01 | 0,08 | ||||
| 0,13 | 9,11 | 82,99 | 746,91 | ||||
| 0,14 | 4,11 | 16,89 | 168,90 | ||||
| Итого | 119,89 | - | - | Σ = 11253,56 | |||
1) Находим среднее ожидаемое значение прибыли(убытка):
А=175*0,09+304*0,02+130*0,04+120*0,14+117*0,09+150*0,12+161*0,13+144*0,14+201*0,07+18*0,01+62*0,05+68*0,10=137,6 тыс.руб.
Б=100*0,10+106*0,16+118*0,21+130*0,09+152*0,06+120*0,11+129*0,13+124* *0,14=119,89 тыс.руб.
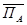 превышает
превышает 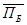 на 17,71 тыс. руб., следовательно вложение капитала А привлекательнее.
на 17,71 тыс. руб., следовательно вложение капитала А привлекательнее.
Для принятия более достоверного решения необходимо определить второй критерий, характеризующий степень риска – колеблемость (изменчивость) возможного результата (прибыли или убытка).
Колеблемость возможного результата представляет собой степень отклонения ожидаемого значения от средней величины. Для этого на практике обычно применяют два тесно связанных критерия: дисперсию и среднеквадратическое отклонение.
Дисперсия 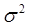 представляет собой среднее взвешенное из квадратов отклонений действительных результатов от среднего ожидаемого и определяется по формуле:
представляет собой среднее взвешенное из квадратов отклонений действительных результатов от среднего ожидаемого и определяется по формуле:
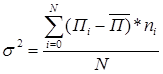 ,
,
где П 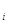 - ожидаемое значение прибыли (убытка) для каждого случая наблюдения;
- ожидаемое значение прибыли (убытка) для каждого случая наблюдения;
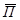 - среднее ожидаемое значение прибыли (убытка).
- среднее ожидаемое значение прибыли (убытка).
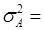 642445,16/310 = 2072,40
642445,16/310 = 2072,40
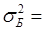 11253,56/69= 163,1
11253,56/69= 163,1
Среднеквадратичное отклонение является мерой абсолютной колеблемости и определяется по формуле:
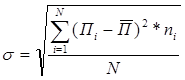
σА = 45,52
σБ = 12,77
Отклонение ожидаемого значения от средней величины у варианта вложения капитала Б привлекательнее.
Относительным критерием, с помощью которого можно сравнить колеблемость возможного результата для разных инвестиционных проектов, является коэффициент вариации V. Он представляет собой отношение среднеквадратического отклонения к среднему ожидаемому значению и определяется по формуле:
V= 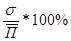 ,
,
где V – коэффициент вариации, выраженный в процентах.
Оценка степени риска на основе коэффициента вариации имеет ряд преимуществ перед другими критериями, поскольку коэффициент вариации – относительная величина и на его размер не оказывают влияние абсолютные значения изучаемого показателя.
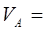 45,52/137,6*100 = 33,08%;
45,52/137,6*100 = 33,08%;
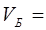 12,77/119,89*100 = 10,65 %.
12,77/119,89*100 = 10,65 %.
Оба варианта и А, и Б находятся в среднем риске вложения капитала и имеют умеренную колеблемость. Однако, у варианта вложения капитала Б коэффициент вариации значительно меньше варианта А.
Вывод.
На основании полученных результатов - среднеквадратичного отклонения и коэффициента вариации, можно сделать вывод, что вариант вложения капитала Б менее рискованный.
ЗАДАНИЕ 5. Расчет страховых платежей по добровольному страхованию риска непогашения кредита
Заемщик взял кредит на определенный срок на условиях погашения. На основе определения кредитоспособности заемщика необходимо рассчитать страховую сумму и страховые платежи поэтапно по добровольному страхованию риска непогашения кредита, выданного хозяйствующему субъекту.
Данные о проценте за кредит, пределе ответственности страховщика, сроках использования кредита заемщиком представлены в таблице 4.
Таблица 4
| Показатель | Вариант № 1 |
| Срок использования кредита заемщиком, мес. | |
| Размер кредита, тыс. руб. | |
| Годовой банковский процент за пользование кредитом, % | |
| Предел ответственности страховщика, % |
Установленные тарифные ставки страховых платежей в зависимости от срока кредита приведены в таблице 5.
Таблица 5
| Срок, в течение которого заемщик пользуется кредитом, месяцы | Установленная тарифная ставка в % от страховой суммы |
| До 6 месяцев | 2,3 |
| До 7 месяцев | 2,4 |
| До 8 месяцев | 2,5 |
| До 9 месяцев | 2,6 |
| До 10 месяцев | 2,8 |
| До 11 месяцев | |
| До 12 месяцев и более | 3,5 |
Исходные данные для оценки риска неплатежеспособности заемщика представлены в таблице 6.
Таблица 6
| Показатель | Вариант № 1 |
| Денежные средства (в кассе, на расчетном счету) тыс. руб. | |
| Ценные бумаги и краткосрочные вложения, тыс. руб. | |
| Краткосрочные кредиты и заемные средства, тыс. руб. | |
| Кредиторская задолженность и прочие пассивы, тыс. руб. |
Решение.
Под кредитоспособностью хозяйствующего субъекта понимается наличие у него предпосылок для получения кредита и способность возвратить предоставленный кредит в срок.
При анализе кредитоспособности заемщика используют ликвидность, которая характеризует способность быстро погашать задолженность. Она определяется соотношением величины задолженности и ликвидных средств, которые могут быть использованы для погашения долгов (наличные деньги, депозиты, ценные бумаги и др.)
Определим коэффициент ликвидности, используя данные таблицы 6, по формуле:
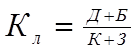 ,
,
где Д – денежные средства;
Б – ценные бумаги и краткосрочные вложения;
К – краткосрочные кредиты и заемные средства;
З – кредиторская задолженность и прочие пассивы.
К = (9400+105448)/(94622+28226) = 114848/122848=0,93.
Коэффициент абсолютной ликвидности находится в промежутке до 1, значит, хозяйствующий субъект является некредитоспособным, т.е. риск неплатежеспособности высокий.
Исходя уровня риска неплатежеспособности хозяйствующего субъекта, для данного заемщика при установлении тарифной ставки для определения страховых платежей, необходимо использовать понижающие и повышающие коэффициенты: 0,7 – 1,0.
Определение страховых платежей произведем в таблице 7.
Таблица 7
| Общая сумма кредита по договору | Выдача кредита | Погашение кредита | Задолженность | Срок пользования кредитом, мес. | Предел ответственности страховщика, % | Страховая сумма, тыс.руб. | Тарифная ставка, % | Сумма страховых платежей, тыс.руб. | |||||
| Дата | Сумма, тыс.руб. | Дата | Сумма, тыс.руб. | Сумма непогашенного кредита, тыс.руб. | Сумма процентов за пользование кредитным товаром,тыс.руб. | Итого | Установленная | Расчетная | |||||
| 15.10.2011 | 2160,00 | 3,5 | 0,29 | ||||||||||
| 15.11.2011 | 16.11.2012 | 276,92 | 3323,08 | 46,52 | 3369,60 | 2021,7 | 3,5 | 0,29 | 5,86 | ||||
| 15.12.2011 | 16.12.2012 | 276,92 | 3046,16 | 42,65 | 3088,81 | 1853,29 | 3,5 | 0,29 | 5,37 | ||||
| 15.01.2012 | 16.01.2013 | 276,92 | 2769,24 | 38,77 | 2808,01 | 1684,81 | 3,5 | 0,29 | 4,89 | ||||
| 15.02.2012 | 16.02.2013 | 276,92 | 2492,32 | 34,89 | 2527,21 | 1516,33 | 3,5 | 0,29 | 4,40 | ||||
| 15.03.2012 | 16.03.2013 | 276,92 | 2215,40 | 31,02 | 2246,42 | 1347,85 | 3,5 | 0,29 | 3,91 | ||||
| 15.04.2012 | 16.04.2013 | 276,92 | 1938,48 | 27,14 | 1965,62 | 1179,37 | 3,5 | 0,29 | 3,42 | ||||
| 15.05.2012 | 16.05.2013 | 276,92 | 1661,56 | 23,26 | 1684,82 | 1010,89 | 3,5 | 0,29 | 2,93 | ||||
| 15.06.2012 | 16.06.2013 | 276,92 | 1384,64 | 19,38 | 1404,02 | 842,41 | 3,5 | 0,29 | 2,44 | ||||
| 15.07.2012 | 16.07.2013 | 276,92 | 1107,72 | 15,51 | 1123,23 | 673,94 | 3,5 | 0,29 | 1,95 | ||||
| 15.08.2012 | 16.08.2013 | 276,92 | 830,80 | 11,63 | 842,43 | 505,46 | 3,5 | 0,29 | 1,47 | ||||
| 15.09.2012 | 16.09.2013 | 276,92 | 553,88 | 7,75 | 561,63 | 336,98 | 3,5 | 0,29 | 0,98 | ||||
| 15.10.2012 | 16.10.2013 | 276,92 | 276,92 | 3,88 | 280,80 | 168,48 | 3,5 | 0,29 | 0,49 | ||||
| 15.11.2012 | 16.11.2013 | 276,92 | 0,00 | 3,5 | 0,29 | 0,00 | |||||||
| Итого | 302,4 | 3,5 | 0,29 | 38,11 |
Сумму непогашенного кредита определяем поэтапно по формуле:
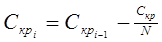 ,
,
где 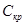 - сумма непогашенного кредита на i – й период;
- сумма непогашенного кредита на i – й период;
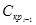 - сумма непогашенного кредита на предшествующий i-тому период;
- сумма непогашенного кредита на предшествующий i-тому период;
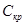 - общая сумма кредита;
- общая сумма кредита;
Скр1 = 3600– 3600/13 = 3323,08. руб.
Скр2 = 3323,08 – 276,92 =3046,16 тыс. руб.
Скр3 = 3046,16 – 276,92 = 2769,24. руб.
Скр4 = 2769,24 – 276,92 = 2492,32 тыс. руб.
Скр5 = 2492,32 – 276,92 =2215,40 тыс. руб.
Скр6 = 2215,40 – 276,92 = 1938,48 тыс. руб.
Скр7 = 1938,48 – 276,92 = 1661,56 тыс. руб.
Скр8 = 1661,56 – 276,92=1384,64 тыс. руб.
Скр9= 1384,64 – 276,92 = 1107,72 тыс. руб.
Скр10 = 1107,72 – 276,92 = 830,80 тыс. руб.
Скр11 = 830,80– 276,92 =553,88 тыс. руб.
Скр12 = 553,88 – 276,92 = 276,92 тыс. руб.
Скр13 = 267,92 – 276,92 = 0,00 тыс. руб.
N- число периодов погашения кредита.
Сумма процентов за пользование кредитом составит:
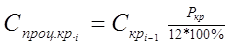 ,
,
где P – годовой банковский процент за пользование кредитом.
Спроц.кр1=3323,08*(17/(12*100%))=46,52
Спроц.кр2=3046,16*(17/(12*100%))=42,65
Спроц.кр3=2769,24*(17/(12*100%))=38,77
Спроц.кр4=2492,32*(17/(12*100%))=34,89
Спроц.кр5=2215,40*(17/(12*100%))=31,02
Спроц.кр6=1938,48*(17/(12*100%))=27,14
Спроц.кр7=1661,56*(17/(12*100%))=23,26
Спроц.кр8=1384,64*(17/(12*100%))=19,38
Спроц.кр9=1107,72*(17/(12*100%))=15,51
Спроц.кр10=830,80*(17/(12*100%))=11,63
Спроц.кр11=553,88*(17/(12*100%))=7,75
Спроц.кр12=276,92*(17/(12*100%))=3,88
Страховая сумма устанавливается пропорционально указанному в договоре страхования проценту ответственности страховщика исходя из всей суммы задолженности по кредиту (включая проценты за пользование кредитом), подлежащей возврату по условиям кредитного соглашения.
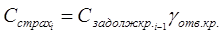 ,
,
где 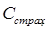 - страховая сумма в i-м периоде, руб.;
- страховая сумма в i-м периоде, руб.;
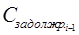 - задолженность по кредиту в i-м периоде, руб.;
- задолженность по кредиту в i-м периоде, руб.;
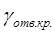 - предел ответственности страховщика.
- предел ответственности страховщика.
С страх .=3600*0,6=2160
С страх .1=3369,60*,06=2021,76
С страх .2=3088,81*0,6=1853,29
С страх .3=2808,01*0,6=1684,81
С страх .4=2527,21*0,6=1516,33
С страх .5=2246,42*0,6=1347,85
С страх .6=1965,62*0,6=1179,37
С страх .7=1684,82*0,6=1010,89
С страх .8=1404,02*0,6=842,41
С страх .9=1123,23*0,6=673,94
С страх .10=842,43*0,6=505,46
С страх .11=561,63*0,6=336,98
С страх .12=280,80*0,6=168,48
Сумму страхового платежа определяют по формуле:
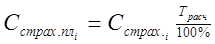 ,
,
где 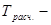 расчетная тарифная ставка на один период в зависимости от графика выплат, оговоренного в кредитном соглашении,
расчетная тарифная ставка на один период в зависимости от графика выплат, оговоренного в кредитном соглашении,
Сстрах.пл.1 = 2021,76*0,29/100 = 5,86 тыс. руб.
Сстрах.пл.2 = 1853,29*0,29/100 = 5,37 тыс. руб.
Сстрах.пл.3 = 1684,81*0,29/100 = 4,89 тыс. руб.
Сстрах.пл.4 = 1516,33*0,29/100 = 4,40 тыс. руб.
Сстрах.пл.5 = 1347,85*0,29/100 = 3,91 тыс. руб.
Сстрах.пл.6 = 1179,37*0,29/100 = 3,42 тыс. руб.
Сстрах.пл.7 = 1010,89*0,29/100 = 2,93 тыс. руб
Сстрах.пл.8 = 842,41*0,29/100 = 2,44 тыс. руб.
Сстрах.пл.9 = 673,94*0,29/100 = 1,95тыс. руб.
Сстрах.пл.10 = 505,46*0,29/100 = 1,47 тыс. руб.
Сстрах.пл.11 = 336,98*0,29/100 = 0,98 тыс. руб.
Сстрах.пл.12 = 168,48*0,29/100 = 0,49 тыс. руб.
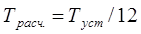
где 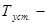 установленная тарифная ставка в зависимости от риска неплатежеспособности заемщика.
установленная тарифная ставка в зависимости от риска неплатежеспособности заемщика.
Туст =3,5 %
Трасч = 3,5/12 = 0,29%
Общая сумма страховых платежей, при добровольном страховании риска от непогашения кредита при высокой степени риска равна: 38,11 тыс.руб.
ЗАДАНИЕ 3. Оценка риска несвоевременной оплаты услуг клиентами при взаимодействии с предприятием.
При взаимодействии с постоянными клиентами, учитывая их финансовые сложности, предприятие не вводит 100% предоплату договоров по оказанию услуг. Однако за последние три года у предприятия при взаимодействии с постоянными клиентами начала расти дебиторская задолженность. В целях сохранения клиентов необходимо определить, при взаимодействии с какими клиентами риск неплатежа со стороны пользователя услуг выше и по отношению к каким клиентам необходимо приостановить оказание услуг до 100% оплаты договоров.
Исходные данные для расчета представлены в таблицах 8 и 9.
Таблица 8
| Вариант № 7 | |
| Порядковые номера клиентов в таблице по выборке №… | 1,2,4 |
| Вариант № 1 | |
| Порядковые номера клиентов в таблице по выборке №… | 6,7,9 |
| Максимально-возможная граница срока неплатежа |
Таблица 9
| Клиент | Данные | ||||||||||||
| Срок задержки, дни | |||||||||||||
| Частота | |||||||||||||
| Срок задержки, дни | |||||||||||||
| Частота | |||||||||||||
| Срок задержки, дни | |||||||||||||
| Частота | |||||||||||||
| Срок задержки, дни | |||||||||||||
| Частота | |||||||||||||
| Срок задержки, дни | |||||||||||||
| Частота | |||||||||||||
| Срок задержки, дни | |||||||||||||
| Частота |
Решение.
Использование договорной системы при взаимодействии клиентов и
предприятия позволяет собрать некоторую информацию о порядочности клиента по отношению к предприятию. В состав такой информации, например, входят графики оплаты договоров, реальные сроки оплаты уже оказанных услуг предприятием или предоплаты (если это оговорено в договоре).
На основании анализа собранных данных о конкретных сроках оплаты оказанных услуг конкретными клиентами можно оценить степень риска несвоевременной оплаты услуг в будущем и принять меры для минимизации потерь, связанных с этим риском.
Параметром вероятностей модели поведения клиента может служить случайная величина, представляющая собой срок задержки клиентом оплаты перевозки. Задержку оплаты будем измерять в днях, прошедших с числа, оговоренного в договоре как крайний срок оплаты. Для получения количественных оценок модели нам необходимо определить функцию распределения вероятностей этой случайной величины, вычислить ее параметры и получить в результате формулу для вычисления вероятности попадания случайной величины (задержка оплаты) в определенный интервал (срок задержки).
Согласно центральной предельной теореме Ляпунова примем, что случайная величина (задержка оплаты) распределена нормально. Тогда на основании данной выборки можно оценить значения дисперсии и математического ожидания анализируемой случайной величины – времени задержки оплаты перевозок, а на основе этих параметров рассчитать степень риска несвоевременной оплаты услуг.
Выборочное среднее рассчитывают по формуле:
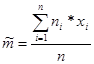 |
,
где 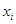 - значения случайной величины (задержка оплаты) Х;
- значения случайной величины (задержка оплаты) Х;
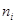 - частоты появления значений
- частоты появления значений 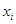 соответственно.
соответственно.
m᷉1=(0*2+4*4+8*3+9*6+12*8+18*2+20*2+24*2+24*2+30*1)/30=11.37
m᷉2=(1*3+2*4+4*3+8*3+10*5+14*6+15*4+20*2)/30=9.27
m᷉4=(12*1+13*1+15*1+17*2+24*6+31*9+46*4+48*4+61*2)/30=33.17
m᷉6=(2*5+10*5+11*4+13*6+14*4+15*5+20*1)/30=11.1
m᷉7=(1*2+3*2+7*4+9*3+10*4+12*5+13*2+14*2+15*1+16*5)/30=10.4
m᷉9=(11*1+18*3+20*2+22*5+24*4+26*6+40*2+41*4+55*2+56*1)/30=29.23
 Исправленную выборочную дисперсию определяют по формуле:
Исправленную выборочную дисперсию определяют по формуле:
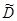 1=[2*(0-11.37)2+4*(4-11.37)2+3*(8-11.37)2+6*(9-11.37)2+8*(12-11.37)2+2*(18-11.37)2+2(20-11.37)2+2*(24-11.37)2+1*(30-11.37)2]/30-1=49.99;
1=[2*(0-11.37)2+4*(4-11.37)2+3*(8-11.37)2+6*(9-11.37)2+8*(12-11.37)2+2*(18-11.37)2+2(20-11.37)2+2*(24-11.37)2+1*(30-11.37)2]/30-1=49.99;
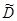 2=[3*(1-9.27)2+4*(2-9.27)2+3*(4-9.27)2+3*(8-9.27)2+5*(10-9.27)2+6*(14-9.27)2+4*(15-9.27)2+2*(20-9.27)2] /30-1= 34.13
2=[3*(1-9.27)2+4*(2-9.27)2+3*(4-9.27)2+3*(8-9.27)2+5*(10-9.27)2+6*(14-9.27)2+4*(15-9.27)2+2*(20-9.27)2] /30-1= 34.13
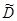 4=[1*12-33.17)2+1*(13-33.17)2+1*(15-33.17)2+2*(17-33.17)2+6*(24-33.17)2+9*(31-33.17)2+ 4*(46-33.17)2+4*(48-33.17)2+2*(61-33.17) 2] /30-1
4=[1*12-33.17)2+1*(13-33.17)2+1*(15-33.17)2+2*(17-33.17)2+6*(24-33.17)2+9*(31-33.17)2+ 4*(46-33.17)2+4*(48-33.17)2+2*(61-33.17) 2] /30-1
=184.21
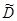 6=[5*(2-11.1)2+5*(10-11.1)2+4*(11-11.1)2+6*(13-11.1)2+4*(14-11.1)2+5*(15-11.1)2 +1*(20-11.1)2] /30-1=21.75
6=[5*(2-11.1)2+5*(10-11.1)2+4*(11-11.1)2+6*(13-11.1)2+4*(14-11.1)2+5*(15-11.1)2 +1*(20-11.1)2] /30-1=21.75
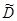 7=[2*(1-10.4)2+2*(3-10.4)2+4*(7-10.4)2+3*(9-10.4)2+4*(10-10.4)2+5*(12-10.4)2+ 2*(13-10.4)2 +2*(14-10.4)2+1*(15-10.4) 2 +5*(16-10.4)2] /30-1=19.63
7=[2*(1-10.4)2+2*(3-10.4)2+4*(7-10.4)2+3*(9-10.4)2+4*(10-10.4)2+5*(12-10.4)2+ 2*(13-10.4)2 +2*(14-10.4)2+1*(15-10.4) 2 +5*(16-10.4)2] /30-1=19.63
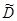 9=[1*(11-29.23)2+3*(18-29.23)2+2*(20-29.23)2+5*(22-29.23)2+4*(24-29.23)2+ 6*(26-29.23)2 +2*(40-29.23)2 +4*(41-29.23)2+2*(55-29.23) 2 +1*(56-29.23)2] /30-1= 142.94
9=[1*(11-29.23)2+3*(18-29.23)2+2*(20-29.23)2+5*(22-29.23)2+4*(24-29.23)2+ 6*(26-29.23)2 +2*(40-29.23)2 +4*(41-29.23)2+2*(55-29.23) 2 +1*(56-29.23)2] /30-1= 142.94
При этом, исправленное среднеквадратическое отклонение имеет вид
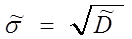
Отсюда:
σ᷉1=7.07
σ᷉2=5.84
σ᷉4=13.57
σ᷉6=4.66
σ᷉7=4.43
σ᷉9=11.96
В задаче необходимо рассчитать доверительные интервалы для количественных параметров распределения 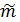 и
и 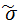 , так как выборочные оценки являются случайными величинами и выборка (n
, так как выборочные оценки являются случайными величинами и выборка (n 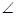 20-30) – небольшая, что увеличивает погрешность в определении значений параметров распределения случайной величины (задержки оплаты).
20-30) – небольшая, что увеличивает погрешность в определении значений параметров распределения случайной величины (задержки оплаты).
Оценка доверительного интервала для параметра нормального распределения характеризуется надежностью 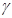 , пределы которой составляют 0,95
, пределы которой составляют 0,95 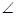
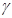
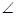 0,999.
0,999.
Для оценки доверительных интервалов математического ожидания нормально распределенной последовательности введем новую случайную величину, построенную по результатам выборки:
1. Результирующий доверительный интервал, покрывающий неизвестный параметр а с надежностью g будет определяться как
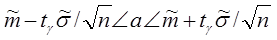
Значения 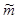 и
и 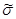 у нас найдены по выборке, а t
у нас найдены по выборке, а t 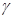 - выбираем из прил.1 по заданным
- выбираем из прил.1 по заданным 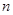 и
и 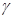 , t
, t 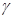 = 2,064
= 2,064

Клиент
(11.37-2.064*7.07) /5.48˂m˂(11.37+2.064*7.07) /5.48
-0.59˂m˂4.74
Клиент
(9.27-2.064*5.84) /5.48˂m˂(9.27+2.064*5.84) /5.48
-0.51˂m˂3.89
Клиент
(33.16-2.064*13.57) /5.48˂m˂(33.16+2.064*13.57) /5.48
0.94˂m˂11.62
Клиент
(11.1-2.064*4.66) /5.48˂m˂(11.1+2.064*4.66) /5.48
0.27˂m˂3.78
Клиент
(10.4-2.064*4.43) /5.48˂m˂(10.4+2.064*4.43) /5.48
0.23˂m˂3.57
Клиент
(29.23-2.064*11.96) /5.48˂m˂(29.23+2.064*11.96) /5.48
0.83˂m˂9.84
2. Искомый доверительный интервал для среднеквадратичного отклонения вычисляется на основе выборки 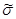 и значения q, который можно найти по таблице прил.2 по заданным n и
и значения q, который можно найти по таблице прил.2 по заданным n и 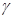 , q = 0,320
, q = 0,320
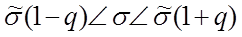
Клиент 1: 7.07(1-0.32) ˂ σ᷉1˂ 7.07(1+0.32)
4.81˂ σ᷉1˂7.71
Клиент 2: 5.84(1-0.32) ˂ σ᷉1˂ 5.84(1+0.32)
3.97˂ σ᷉1˂7.71
Клиент 4: 13.57(1-0.32) ˂ σ᷉1˂ 13.57(1+0.32)
9.23˂ σ᷉1˂17.91
Клиент 6: 4.66(1-0.32) ˂ σ᷉1˂ 4.66(1+0.32)
3.17˂ σ᷉1˂6.15
Клиент 7: 4.43(1-0.32) ˂ σ᷉1˂ 4.43(1+0.32)
3.01˂ σ᷉1˂5.85
Клиент 9: 11.96(1-0.32) ˂ σ᷉1˂ 11.96(1+0.32)
8.13˂ σ᷉1˂15.79
Найдя интервалы, в которых может находиться значение математического ожидания и среднеквадратичного отклонения, мы можем уточнить искомое значение вероятности задержки клиентом оплаты перевозок. Для этого необходимо, исходя из полученных диапазонов колебания значений параметров выборки, используя выражение:
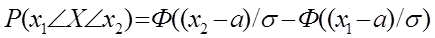
вычислить минимальную и максимальную вероятности. При вычислении максимальной и минимальной вероятностей необходимо учитывать четность функции Ф и тот факт, что под максимальным и минимальным аргументом функции понимается максимальное и минимальное
абсолютные значения аргумента. В качестве окончательного результата взять среднее значение максимальной и минимальной вероятностей:
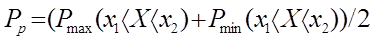
 2015-07-14
2015-07-14 1167
1167








