Источник: http://vtit.kuzstu.ru/books/shelf/15/doc/p1.html
Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.
Необходимость рассмотрения подобных задач обусловлена различными причинами. Одной из основных является та, что исходные данные для численного решения любой реальной задачи оптимизации в большинстве случаев определяются приближенно или могут изменяться под влиянием каких-то факторов, что может существенно сказаться на оптимальности выбираемой программы (плана) действий. Соответственно, разумно указывать не конкретные данные, а диапазон возможного изменения данных, чтобы в результате решения иметь наилучшие планы для любого варианта исходных данных.
С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.
Заметим, что существуют различные подходы к подобному анализу (например, на основе постановки двойственной задачи). Здесь мы, не ссылаясь на двойственные оценки, рассмотрим самые простейшие варианты решения для самых простейших параметрических программ.
1) Рассмотрим задачу параметрического линейного программирования, в которой только коэффициенты целевой функции линейно зависят от некоторого единственного параметра λ (времени, температуры и т. п.):
Отыскать максимум (или минимум) функции:
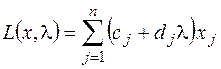 (12.1)
(12.1)
при условиях:
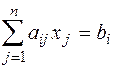 ,
, 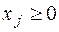 ,
, 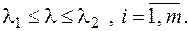 (12.2)
(12.2)
Если обратиться к геометрической интерпретации задачи, то можно заметить, что вектор-градиент линейной формы определяется её параметром. Например, для целевой функции
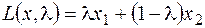
при различных значениях параметра λ градиент определяет различные направления роста функции.
На рисунке нетрудно видеть, что, если при некотором значении параметра максимум достигается в вершине A, то небольшая вариация этого значения несколько изменит направление градиента, но не изменит положение точки максимума. Отсюда напрашивается вывод, что некоторый план, оптимальный при при 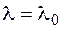 оптимален и в окрестности
оптимален и в окрестности 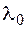 , т. е. при
, т. е. при 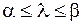 , где
, где 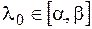 .
.
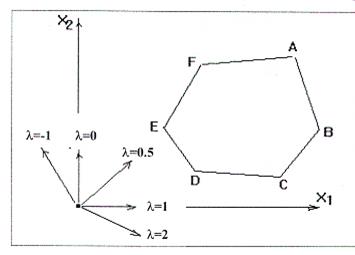
Рис. 12.1
Можно заметить, что при градиенте, ставшем перпендикулярным некоторой стороне многоугольника планов, имеем два разных оптимальных опорных плана с одним и тем же значением линейной формы, откуда можно утверждать непрерывность экстремума линейной формы по λ.
В случае неограниченности множества планов можно утверждать, что если линейная форма не ограничена при 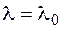 , то она не ограничена при всех λ, больших или меньших
, то она не ограничена при всех λ, больших или меньших 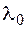 .
.
Алгоритм для решения задач параметрического линейного программирования в случае зависимости от параметра коэффициентов целевой функции (примеры решения подобных задач приведены ниже):
1. Вначале решается задача (12.1)-(12.2) прямым симплекс методом, и вместо 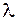 подставляем удобное нам число из заданного промежутка
подставляем удобное нам число из заданного промежутка 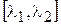 , но не заменяем
, но не заменяем 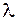 конкретным числом.
конкретным числом.
2. Получив оптимальный план 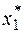 (все
(все 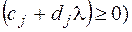 ), отбрасываем промежуток, для которого этот план оптимален. И продолжаем решение полученной симплекс таблицы для тех
), отбрасываем промежуток, для которого этот план оптимален. И продолжаем решение полученной симплекс таблицы для тех 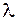 , для которых план
, для которых план 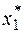 не является оптимальным. Получив оптимальный план
не является оптимальным. Получив оптимальный план 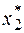 , отбрасываем промежуток, для которого этот план оптимален. Решение продолжается до тех пор, пока для всех
, отбрасываем промежуток, для которого этот план оптимален. Решение продолжается до тех пор, пока для всех 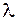 не будет найден оптимальный план или установлено, что задача не разрешима.
не будет найден оптимальный план или установлено, что задача не разрешима.
2) В случае зависимости от параметра компонент вектора правых частей ограничений, т. е. решения задачи поиска экстремума функции
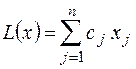 (12.3)
(12.3)
при условиях:
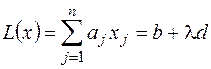 ,
, 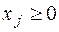 ,
, 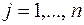 ;
; 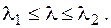 (12.4)
(12.4)
Алгоритм решения задачи в случае зависимости от параметра компонент вектора правых частей ограничений:
1. Вначале решается задача (12.3)-(12.4) двойственным симплекс методом, и вместо 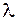 подставляем удобное нам число из заданного промежутка
подставляем удобное нам число из заданного промежутка 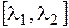 , но не заменяем
, но не заменяем 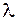 конкретным числом.
конкретным числом.
2. Получив оптимальный план 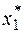 (все
(все 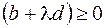 ), отбрасываем промежуток, для которого этот план оптимален. И продолжаем решение полученной симплекс таблицы для тех
), отбрасываем промежуток, для которого этот план оптимален. И продолжаем решение полученной симплекс таблицы для тех 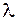 , для которых план
, для которых план 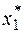 не является оптимальным. Получив оптимальный план
не является оптимальным. Получив оптимальный план 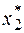 , отбрасываем промежуток, для которого этот план оптимален. Решение продолжается до тех пор, пока для всех
, отбрасываем промежуток, для которого этот план оптимален. Решение продолжается до тех пор, пока для всех 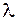 не будет найден оптимальный план или установлено, что задача не разрешима.
не будет найден оптимальный план или установлено, что задача не разрешима.
Во избежание сложностей, связанных с требованием сохранения неотрицательности компонент плана при любых λ (сохранения неотрицательности правой части системы уравнений при всех ее тождественных преобразованиях), достаточно постановить двойственную задачу, воспользоваться вышеупомянутым алгоритмом решения задач параметрического линейного программирования при зависимости от параметра коэффициентов целевой функции и с помощью известных двойственных соотношений находить решение исходной задачи.
Пример 12.1. Рассмотрим задачу минимизации
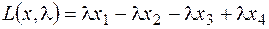
при условиях
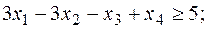
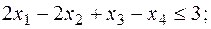
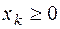 ,
, 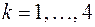 ;
; 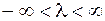 .
.
Решение. Как обычно, приводим задачу к канонической форме и с использованием метода искусственного базиса отыскиваем начальный опорный план 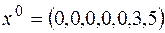 c
c 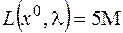 .
.
| С баз | Базис 1 | План Хбаз | λ | -λ | -1 | М | |||
| А1 | А2 | А3 | А4 | А5 | А6 | А7 | |||
| М | А7 | -3 | -1 | -1 | |||||
| А6 | -2 | -1 | |||||||
| Δk | 5М | 3М- λ | -3М+ λ | -М+1 | М-1 | -М |
Так как определяющую роль на этом шаге решения играет величина M, превышающая все величины задачи, то не обращаем внимания на 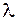 и, обнаружив невыполнение критерия оптимальности для
и, обнаружив невыполнение критерия оптимальности для 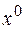 , вводим в базис
, вводим в базис 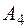 вместо
вместо 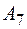 (переходим к следующему опорному плану):
(переходим к следующему опорному плану):
| С баз | Базис 2 | План Хбаз | λ | -λ | -1 | |||
| А1 | А2 | А3 | А4 | А5 | А6 | |||
| А4 | -3 | -1 | -1 | |||||
| А6 | -5 | -1 | ||||||
| Δk | 3 - λ | -3 + λ | -1 |
Полученный опорный план 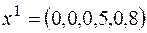 c
c 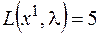 будет оптимальным, если все значения
будет оптимальным, если все значения 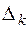 неположительны, т. е.
неположительны, т. е.
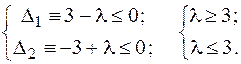
Решаем систему двух линейных неравенств и обнаруживаем, что найденный план 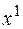 оптимален при
оптимален при 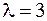 .
.
Исследуем оставшиеся из заданного диапазона значения λ.
Пусть 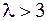 . Тогда
. Тогда 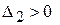 и вектор
и вектор 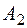 подлежит вводу в базис, но в силу неположительности его компонент приходим к выводу, что при
подлежит вводу в базис, но в силу неположительности его компонент приходим к выводу, что при 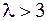 линейная форма задачи не ограничена снизу.
линейная форма задачи не ограничена снизу.
Пусть 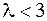 . Тогда
. Тогда 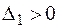 и в базис вводится вектор
и в базис вводится вектор 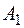 :
:
| С баз | Базис 3 | План Хбаз | λ | -λ | -1 | |||
| А1 | А2 | А3 | А4 | А5 | А6 | |||
| А4 | 1/5 | -1 | -2/5 | -3/5 | ||||
| λ | А1 | 8/5 | -1 | -1/5 | 1/5 | |||
| Δk | (8λ+1)/5 | -(λ+2)/5 | (λ-3)/5 |
Полученный опорный план является оптимальным, если все значения 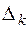 неположительны, т. е.
неположительны, т. е.
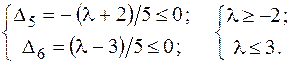
Решая эту систему линейных неравенств, обнаруживаем, что найденный план 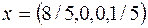 c
c 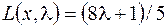 оптимален при
оптимален при 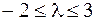 .
.
Пусть 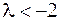 . Тогда
. Тогда 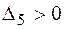 и вектор
и вектор 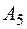 подлежит вводу в базис; в силу неположительности его компонент приходим к выводу, что при
подлежит вводу в базис; в силу неположительности его компонент приходим к выводу, что при 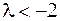 линейная форма задачи не ограничена снизу.
линейная форма задачи не ограничена снизу.
Таким образом, мы получили решение задачи:
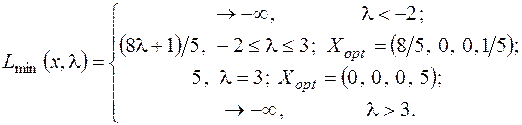
Пример 12.2. Рассмотрим задачу максимизации
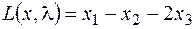
при условиях
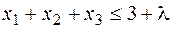 ;
;
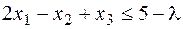 ;
;
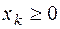 ,
, 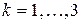 ;
; 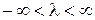 .
.
Решение. Чтобы решить эту задачу, достаточно решить двойственную к ней задачу, имеющую вид:
минимизировать
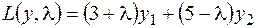
при условиях
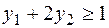 ;
;
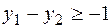 ;
;
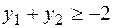 ;
;
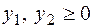 ;
;
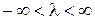 .
.
Данная задача будет решаться с помощью прямого симплекс метода. Приводим двойственную задачу к канонической форме (умножив предварительно второе и третье неравенства на (-1)) и начинаем обычное решение обычным симплексным методом. Заметьте, что указанное умножение тождественно смене знака у переменных 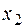 и
и 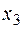 исходной задачи.
исходной задачи.
| С баз | Базис 1 | План Yбаз | 3+ λ | 5-λ | M | |||
| А1 | А2 | А3 | А4 | А5 | А6 | |||
| M | А6 | -1 | ||||||
| А4 | -1 | |||||||
| А5 | -1 | -1 | ||||||
| Δ k | M | M-3-λ | 2M-5+λ | -M |
| С баз | Базис 2 | План Yбаз | 3+λ | 5-λ | M | ||||
| А1 | А2 | А3 | А4 | А5 | А6 | ||||
| 3+λ | А1 | -1 | |||||||
| А4 | -1 | ||||||||
| А5 | -1 | ||||||||
| zk | 3+λ | 3+λ | 6+2λ | -(3+λ) | 3+λ | ||||
| Δ k | 1+3λ | -(3+λ) | 3+λ-M | ||||||
Найденный план 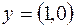 оптимален, если
оптимален, если 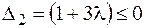 и
и 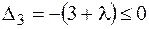 , т. е. при
, т. е. при 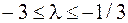 ,
, 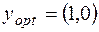 .В строке
.В строке 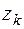 (в позициях 6, 4, и 5 в соответствии с начальным базисом) находим решение прямой задачи:
(в позициях 6, 4, и 5 в соответствии с начальным базисом) находим решение прямой задачи: 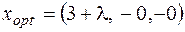 ,
, 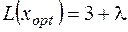 .
.
Пусть 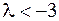 . Попытка ввода в базис вектора
. Попытка ввода в базис вектора 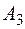 обнаруживает, что в этом случае линейная форма решаемой (двойственной) задачи не ограничена снизу и, следовательно, ограничения исходной задачи противоречивы.
обнаруживает, что в этом случае линейная форма решаемой (двойственной) задачи не ограничена снизу и, следовательно, ограничения исходной задачи противоречивы.
В случае 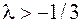 имеем:
имеем:
| С баз | Базис 3 | План Yбаз | 3+λ | 5-λ | M | ||||
| А1 | А2 | А3 | А4 | А5 | А6 | ||||
| 5-λ | А2 | 1/2 | 1/2 | -1/2 | 1/2 | ||||
| А4 | 1/2 | -3/2 | 1/2 | -1/2 | |||||
| А5 | 5/2 | -1/2 | -1/2 | 1/2 | |||||
| zk | (5-λ)/2 | (5-λ)/2 | 5-λ | -(5-λ)/2 | (5-λ)/2 | ||||
| Δ k | -(3λ+1)/2 | -(5-λ)/2 | -M+… | ||||||
Решаем систему неравенств 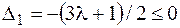 ,
, 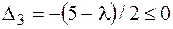 . Обнаруживаем, что при
. Обнаруживаем, что при 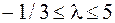 ,
, 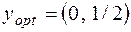 ,
, 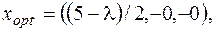
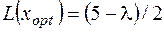 .
.
Продолжаем решение задачи при 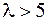 . Получаем:
. Получаем:
| С баз | Базис 4 | План Yбаз | 3+λ | 5-λ | M | ||||
| А1 | А2 | А3 | А4 | А5 | А6 | ||||
| 5-λ | А2 | -1 | |||||||
| А4 | -3 | -1 | |||||||
| А5 | -2 | ||||||||
| zk | 5-λ | -(5-λ) | 5-λ | 5-λ | |||||
| Δ k | -8 | 5-λ | -M | ||||||
Видим, что при 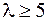 ,
, 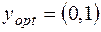 ,
, 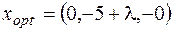 ,
, 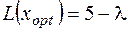 . Задача решена:
. Задача решена:
| Диапазон λ | Сопряженная задача | Исходная задача |
| λ <-3 | L(y, λ)→ - ∞ | Ограничения противоречивы |
| -3≤λ≤-1/3 | yopt = (1,0) | xopt = (3+ λ,0,0), L(xopt) =3+ λ |
| -1/3≤λ≤5 | yopt = (0,1/2) | xopt =((5- λ)/2,0,0), L(xopt)=(5- λ)/2 |
| λ≥5 | yopt = (0,1) | xopt = (0,-5+ λ,0), L(xopt)=5- λ |
Увы, в случае зависимости от параметра компонент матрицы ограничений столь простого универсального подхода к решению не существует. Нет простых решений и в случае зависимости характеристик задачи от нескольких параметров.
Варианты заданий для самостоятельной работы
Решить задачу параметрического линейного программирования. Объяснить полученные результаты.
1.
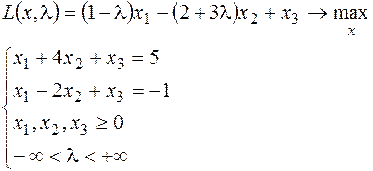
2.
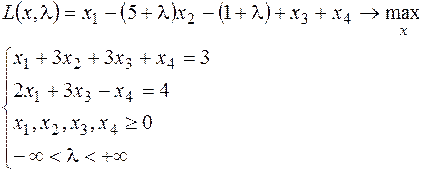
3.
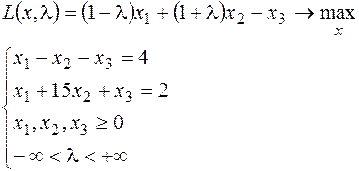
4.
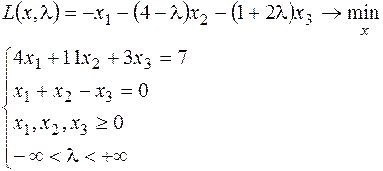
5.
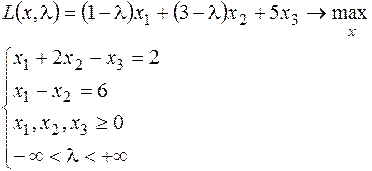
6.
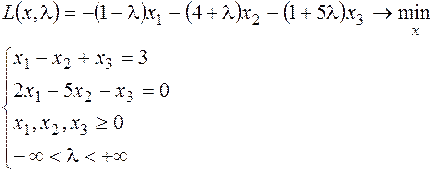
7.
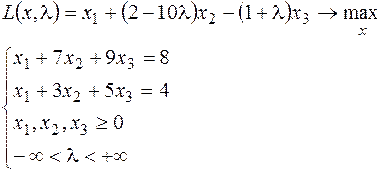
8.
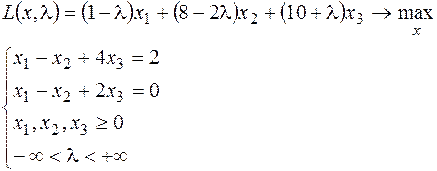
9.
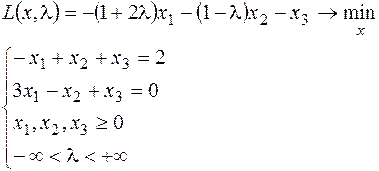
10.
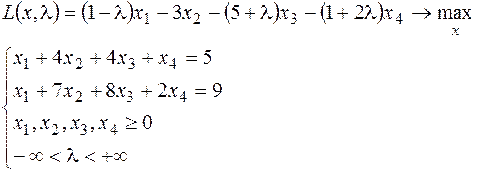
11.
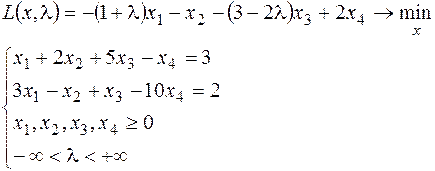
12.
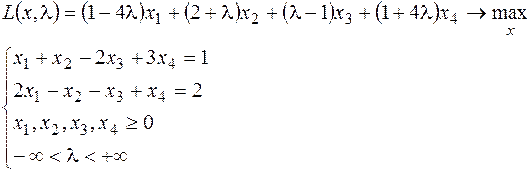
13.
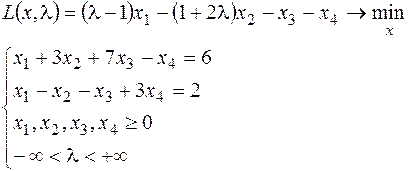
14. Максимизировать
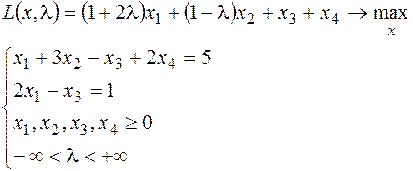
15. Максимизировать
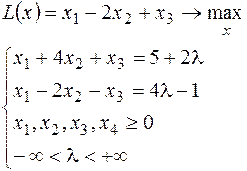
16.
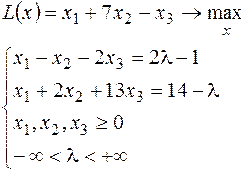
17.
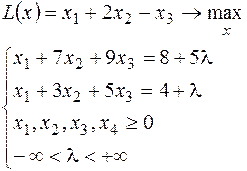
18.
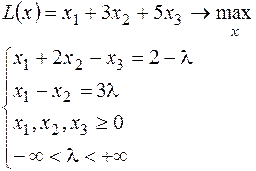
19.
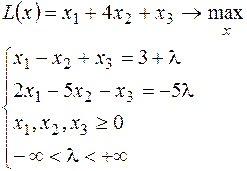
20.
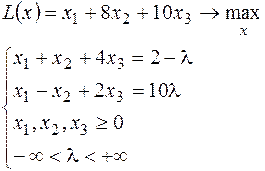
21.
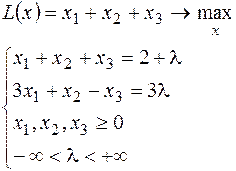
22.
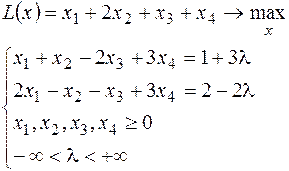
23.
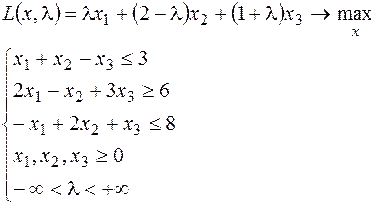
24.
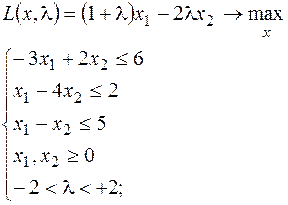
25.
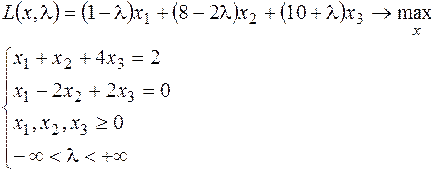
26. Минимизировать
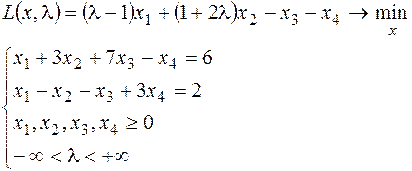
27.
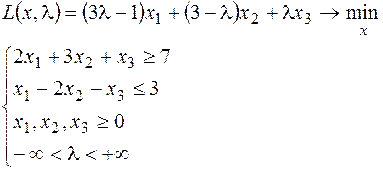
28.
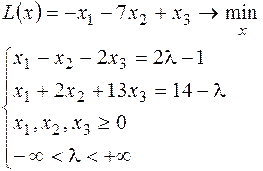
29.
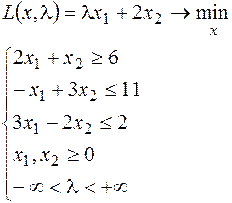
30.
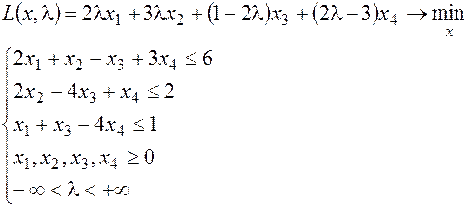
31.
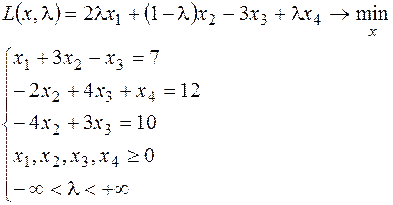
32.
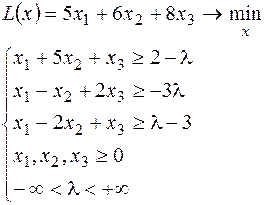
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Акулич И.Л. Математическое программирование в примерах и задачах.
1. Тынкевич М.А. Экономико-математические методы (исследование операций). - Кемерово: КузГТУ, 2000.
2. Гольштейн Е.Г. Линейное программирование / Е. Г. Гольштейн, Д.Б.Юдин.. -М.:Наука, 1969.
 2015-08-13
2015-08-13 3749
3749






