Цепь переменного тока с параллельным соединением RLC — элементов: резонанс токов и способы его достижения

I(a1) Ua1 I1

I2 I(a2)

Ua2

φ φ

Iр(L) Iр(С)

X_L = Xc

Имеем:

b_L = bc (проводимость)

I_L= Ic= I1p = I2p — max

Признак:

(W I²) / 2 = (W U²) / 2

Колеблется внутри контура (в идеале) не выходя за пределы, а так как r = 0 никуда не расходуется. Ток в общей цепи равен нулю (0), а в реальном контуре расходуется энергия на активном сопротивлении и расходуемая часть пополняется источником I стремится к нулю — min.

Свойство: имеем резонанс токов.

Имеем резонанс токов с переводом цепи в индуктивный или емкостной режимы.

В цепи, схема которой содержит параллельно соединенные индуктивный, емкостный и резистивный элементы, т. е. параллельный контур может возникнуть резонанс токов.

При заданном напряжении питания общий ток

i=Y = — комплексная проводимость параллельного контура; где Y - полная проводимость контура.

При угловой частоте ω_рез = l/ индуктивная b_L == 1/ωL и емкостная Ь_c = С проводимости параллельных ветвей одинаковые, аргумент комплексной проводимости цепи — φ равен нулю, полная проводимость контура минимальна: у = g и общий ток минимальный: I_рез = gU.

Режим параллельного контура, при котором сдвиг фаз между напряжением и общим током равен нулю, называется резонансом токов.

При резонансе действующие значения токов в индуктивном и емкостном эле­ментах одинаковые, а сдвиг фаз между токами равен π, так как ток в индуктивном элементе отстает от напряжения по фазе на угол л/2, а ток в емкостном элементе опережает напряжение на такой же угол π/2 ).

На рис. 2.49 показаны резонансные кривые параллельного контура. В емкост­ном элементе ток I_с возрастает пропорционально угловой частоте, в индук­тивном элементе ток l_L обратно пропорционален угловой частоте, в резистивном элементе ток l_r — U/r от угловой частоты не зависит. Точка пересечения кривых /_с(ω) и J_L (ω) соответствует резонансу токов, при котором I=I_r.

Если проводимость g резистивного элемента равна нулю, то и полная проводимость у цепи при резонансе равна нулю и общий ток иде­ального параллельного контура (ток источника) равен нулю, что эквивалентно размыканию цепи.

Последовательно с индуктивным элементом L может быть включен резистивный элемент r_L, а последовательно с емкостным элементом С — резистивный элемент г_с учитывающие, например, потери энергии в проводах. Условием резонанса токов в такой цепи будет равенство индуктивной и емкостной проводимостей этих ветвей.

И в этом случае при резонансе общий ток совпадает по фазе с напряжением. Отметим, что резонанс токов в отличие от резонанса напряжений — явление безопасное для электроэнергетических установок. Большие токи в ветвях при ре­зонансе токов возникают лишь в случае больших реактивных проводимостях ветвей, т. е. больших емкостей конденсаторов и малых индуктивностей катушек. Ничего неожиданного здесь нет, так как токи в обеих ветвях взаимно независимы и их зна­чения определяются (на основании закона Ома) приложенным напряжением.

18 резонанс токов в однофазных цепях синусоидального тока.

19 представление активных, реактивных и полных сопротивлений действительными числами, треугольниками, комплексными числами.

20 комплексный метод расчета синусоидальных цепей со сложным соединением элементов.

КОМПЛЕКСНЫЙ МЕТОД РАСЧЕТА ЦЕПЕЙ
СИНУСОИДАЛЬНОГО ТОКА

Понятия комплексных токов и напряжений 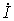, , 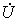комплексных сопротивлений и проводимостей Z и Y лежат в основе комплексного метода расчета цепей синусоидального тока.

Для расчета цепи необходимо перейти от заданных характеристик действующих в цепи источников ЭДС и тока, используя формулы прямого преобразования (7.1), к их комплексным изображениям: 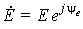; 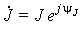(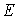, 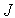— действующие ЭДС и токи, y _e, y _J — их начальные фазы). При наличии единственного источника его начальную фазу можно принять равной нулю, тогда его комплексное изображение будет вещественным. Далее вводятся комплексные сопротивления (или проводимости) элементов цепи: Z_R = R; Z_L = j w L; Z_C = 1/ j w C или Y_R = 1/ R; Y_L = 1/ j w L; Y_C = j w C. Эти величины выражают связи комплексных токов 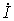и напряжений 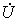на элементах цепи: 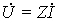(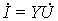). Сами комплексные токи и напряжения подчиняются законам Кирхгофа: 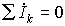; 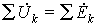. Поэтому далее комплексные величины рассчитываются на основе уравнений Кирхгофа либо вытекающих из них узловых или контурных уравнений. При этом матрицы узловых проводимостей Y _у или контурных сопротивлений Z _к, формируемые из комплексных проводимостей или сопротивлений элементов цепи, имеют комплексные элементы.

К комплексным величинам 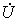и 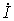можно применять принципы наложения и взаимности. Комплексные сопротивления Z и проводимости Y подчиняются правилам суммирования и преобразования при последовательном и параллельном соединениях, тождественным правилам преобразованиям сопротивлений R и проводимостей G резистивных элементов.

Таким образом, комплексный метод позволяет распространить на расчет цепей синусоидального тока все известные способы и методы расчета резистивных цепей. Их соответствие расчетным величинам и формулам комплексного метода показано в Tабл. 7.2.

Значения комплексных токов 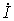и напряжений 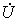определяют действующие значения как модуль соответствующей комплексной величины (или его амплитуду, если при анализе используются комплексные амплитуды). Начальная фаза равна аргументу соответствующей комплексной величины. Таким образом, для перехода от комплексных изображени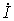й и 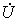к представлению искомых величин во временной области i (t) и u (t) используются формулы обратного преобразования (7.2).

Обозначения величин и соотношений

Величины, законы и методы	При анализе резистивных цепей во временной области	При комплексном анализе на синусоидальном токе
ЭДС	e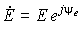
Ток источника	J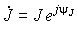
Напряжение	u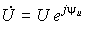
Ток	i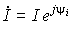
Сопротивление	R	Z = R + jX
Проводимость	G	Y = G – jB
Закон Ома	u = Ri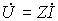
“ “	i = Gu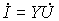
1-й закон Кирхгофа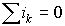
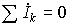
2-й закон Кирхгофа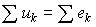
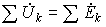
Узловые уравнения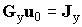
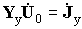
Контурные уравнения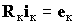

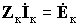
21 основные определения переменного тока: частота, амплитуда, начальная фаза, сдвиг фаз.