1. Обчислити інтеграли методом безпосереднього інтегрування
а) 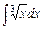 , б)
, б) 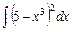 , в)
, в) 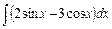 , г).
, г). 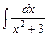
Розв'язання. а. За формулою 2 з таблиці невизначених інтегралів для 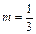 дістаємо
дістаємо
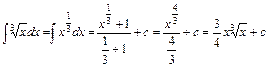 ;
;
б. Розкриємо дужки під знаком інтеграла і за формулою для 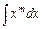 визначаємо
визначаємо
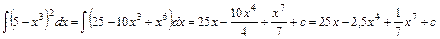 ;
;
в. Згідно з властивостями 3 і 4 невизначеного інтеграла і табличними інтегралами маємо
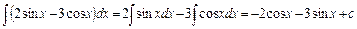 .
.
г. За формулою 9 із таблиці невизначених інтегралів для 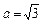 дістаємо
дістаємо
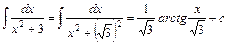 .
.
2. Обчислити інтеграл методом заміни змінної під знаком інтеграла (підстановки) та здійснити перевірку правильності знаходження інтеграла.
а) 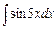 , б)
, б) 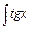 , в)
, в) 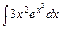 ,
,
г) 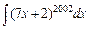 , д)
, д) 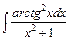 , е)
, е) 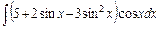 .
.
Розв'язання. а. Здійснимо заміну змінної 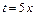 . Тоді
. Тоді 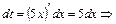
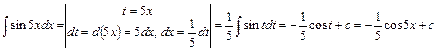 .
.
Щоб перевірити, чи правильно знайдено інтеграл знайдемо похідну від результату інтегрування:
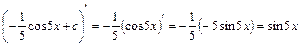 .
.
Отже, інтеграл знайдено правильно.
б. У цьому прикладі застосуємо перетворення над підінтегральною функцією 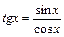 , а потім здійснимо заміну змінної
, а потім здійснимо заміну змінної 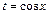 :
:
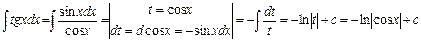 .
.
Перевірка: 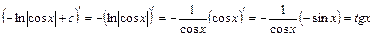 . Інтеграл знайдено правильно.
. Інтеграл знайдено правильно.
в. 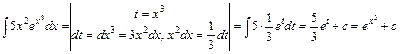 .
.
Перевірка: 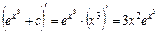 .
.
г. 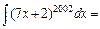
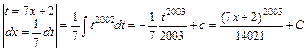 .
.
Перевірка: 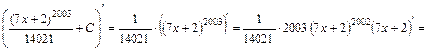
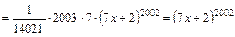 .
.
д. Врахувавши, що 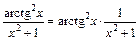 та
та 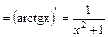 , здійснимо заміну змінної під знаком інтеграла t= arctg x:
, здійснимо заміну змінної під знаком інтеграла t= arctg x:
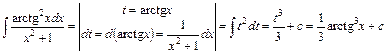 .
.
Перевірка: 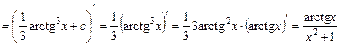 .
.
е. Для цього інтеграла слід врахувати, що 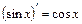 та здійснити заміну t= sin x:
та здійснити заміну t= sin x:
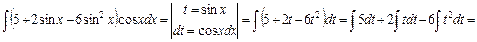
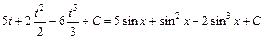 .
.
Перевірка: 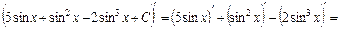
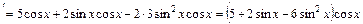 .
.
3. Обчислити інтеграл методом інтегрування за частинами:
а) 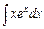 , б)
, б) 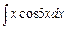 , в)
, в) 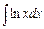 , г)
, г) 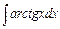 ,
,
д) 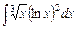 , е)
, е) 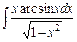 .
.
Розв'язання. а. Щоб скористатись базовою формулою (5.3) позначимо: 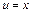 ,
, 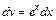 . Тоді
. Тоді 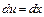 ,
, 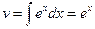 . Підставивши
. Підставивши 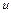 ,
, 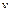 і
і 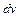 у праву частину базової формули дістанемо
у праву частину базової формули дістанемо
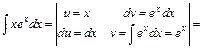
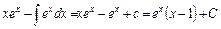 .
.
Якщо ж позначити: 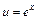 ,
, 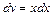 , то дістанемо
, то дістанемо 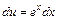 ,
, 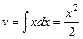 , та
, та
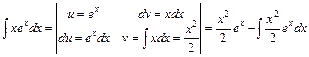 .
.
Інтеграл справа 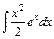 став складнішим ніж інтеграл зліва
став складнішим ніж інтеграл зліва 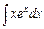 . Тому в методі інтегрування частинами підінтегральний вираз
. Тому в методі інтегрування частинами підінтегральний вираз 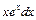 недоцільно представляти у вигляді добутку udv, якщо
недоцільно представляти у вигляді добутку udv, якщо 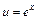 та
та 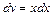 .
.
б. Позначимо: 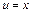 ,
, 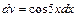 . Тоді
. Тоді 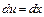 ,
, 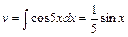 . Підставивши
. Підставивши 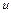 ,
, 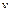 і
і 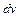 у праву частину базової формули (5.3) дістанемо
у праву частину базової формули (5.3) дістанемо
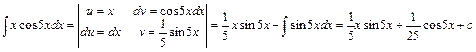 ;
;
в) 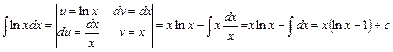 ;
;
г) У цьому прикладі застосовується спочатку метод інтегрування частинами, а потім метод підстановки:
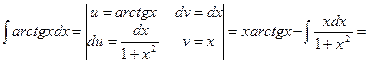
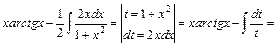
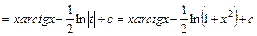 .
.
д) У розглядуваному випадку інтегрування за частинами потрібно застосувати кілька разів:
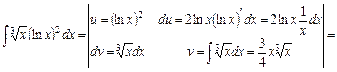
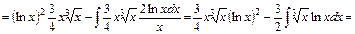
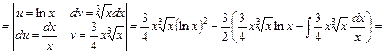
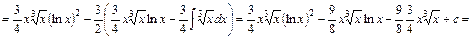
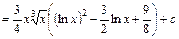 .
.
е) 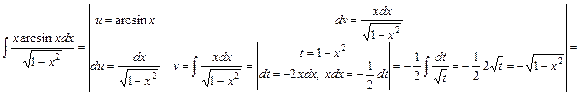
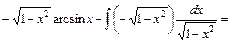
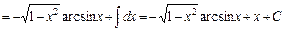 .
.
 2015-08-13
2015-08-13 305
305







