Определение 9.1. Линейное пространство V называется евклидовым, если каждой паре векторов x, y из V поставлено в соответствие действительное число (x, y), называемое скалярным произведением, удовлетворяющее следующим аксиомам:
1°. (x, y) = (y, x), 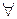 x, y
x, y 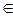 V.
V.
2°. (x + y, z) = (x, z) + (y, z), 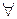 x, y, z
x, y, z 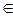 V.
V.
3°. ( x, y) =
x, y) =  (x, y),
(x, y), 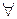 x, y
x, y 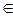 V,
V, 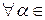 R.
R.
4°. (x, x) 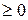 ,
, 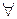 x
x 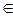 V; (x, x) = 0
V; (x, x) = 0 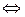 x = 0.
x = 0.
В дальнейшем, если не оговорено особо, будут рассматриваться евклидовы пространства конечной размерности n.
Приведем примеры конкретных евклидовых пространств.
Пример 1. Рассмотрим пространство R 3 свободных векторов, в котором скалярное произведение двух векторов x и y определяется, как в §2.4. Оно удовлетворяет аксиомам 1°–4°. Поэтому R 3 – евклидово пространство.·
Пример 2. Пусть е l, е 2,..., е n – базис линейного пространства V. Для любых векторов x и y этого пространства, заданных разложениями вида (8.7)
x = x 1 е l + x 2 е 2 +... + x n е n = (x 1, x 2,…, xn),
y = y 1 е l + y 2 е 2 +... + y n е n = (y 1, y 2,…, yn),
введем скалярное произведение по формуле
(x, y) = 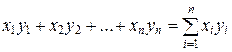 . (9.1)
. (9.1)
В частности, в линейном пространстве R n формула (9.1) также определяет скалярное произведение, превращая его тем самым в евклидово пространство R n.
|
|
|
Проверка справедливости аксиом 1°–4° не представляет труда. Следовательно, линейное пространство V, а значит, и R n со скалярным произведением, заданным формулой (9.1), является евклидовым.·
Из аксиом 2° и 3° скалярного произведения следует, что если y =  y 1 + +
y 1 + +  y 2 +... +
y 2 +... + 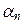 y n, где
y n, где  ,
,  ,...,
,..., 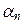 – числа из R, а y 1, y 2,…, y n – векторы из V, то
– числа из R, а y 1, y 2,…, y n – векторы из V, то
(x, y) = (x,  y 1 +
y 1 +  y 2 +... +
y 2 +... + 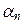 y n) =
y n) =  (x, y 1) +
(x, y 1) +  (x, y 2) +… +
(x, y 2) +… + 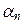 (x, y n) =
(x, y n) = 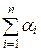 (x, y i).
(x, y i).
 2015-08-21
2015-08-21 1033
1033








