Золотое сечение в математике

В математике пропорцией (лат. proportio) называют равенство двух отношений: а: b = с: d.

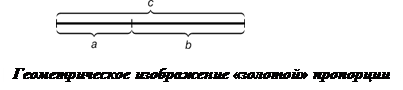Любой отрезок прямой можно разделить на две части в любом отношении. Существует разбиение отрезка на две неравные части, при котором меньший отрезок так относится к большему, как больший относится ко всему отрезку или весь отрезок так относится к большей части, как сама большая часть относится к меньшей. Такое разбиение называют золотым сечением или золотой пропорцией. a: b = b: c или с: b = b: а

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

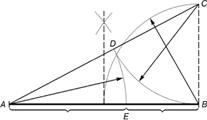
Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок СD, равный отрезку ВС. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью. Если АВ принять за единицу, то AE = 0,618..., ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Замечательный пример «Золотого сечения» представляет собой правильный пятиугольник – выпуклый и звёздчатый (пентаграмма).

Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471 - 1528). Пусть О – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC.

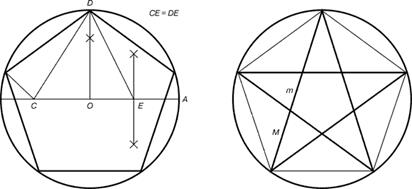
Откладываем на окружности отрезки DC и получим пять точек для построения правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией. Внутри вновь получающихся пятиугольников можно продолжать строить новые пятиугольники, при этом отношение длин отрезков будет сохраняться.

Каждый конец пятиугольной звезды представляет собой «золотой» треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

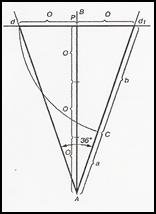Построение золотого треугольника начинается с проведения прямой АВ. От точки А откладываем на ней три раза отрезок О

произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезок О. Полученные точки d и d ₁ соединяем прямыми с точкой А. Отрезок dd ₁ откладываем на линию Ad ₁, получая точку С. Она разделила линию Ad ₁ в пропорции золотого сечения. Линиями Ad ₁ и dd ₁ пользуются для построения «золотого» прямоугольника.

«Золотой» прямоугольник

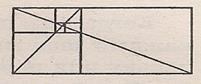Древние греки считали, что прямоугольники, стороны которых образуютзолотое сечение, имеют наиболее приятную для глаз форму. У таких золотых прямоугольников длина больше ширины в 0,618 раз.

Если от золотого прямоугольника отрезать квадрат,

«Золотой» кубоид

то снова получится золотой прямоугольник. Этот процесс можно продолжать до бесконечности. А если провести диагональ первого и второго прямоугольника, то точка их пересечения будетпринадлежать всем получаемым золотым прямоугольникам.

Есть и «золотой» кубоид - это прямоугольный параллелепипед с ребрами, имеющими длины 1,618; 1 и 0,618.