Лабораторная работа № 5
Определение моментов инерции тел произвольной формы
Цель работы
Определение момента инерции математического и физического маятника, а также изучение зависимости момента инерции физического маятника от распределения массы.
Теоретическая часть
Основное уравнение динамики вращательного движения тела вокруг неподвижной оси имеет вид:
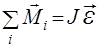 , (1)
, (1)
где 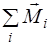 – векторная сумма моментов всех сил относительно оси вращения,
– векторная сумма моментов всех сил относительно оси вращения, 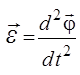 – угловое ускорение тела, т.е. вторая производная по времени от угла поворота φ тела. Соотношение (1) аналогично 2 – му закону Ньютона в динамике поступательного движения и в таком виде записывается в тех случаях, когда момент инерции тела при вращении не изменяется.
– угловое ускорение тела, т.е. вторая производная по времени от угла поворота φ тела. Соотношение (1) аналогично 2 – му закону Ньютона в динамике поступательного движения и в таком виде записывается в тех случаях, когда момент инерции тела при вращении не изменяется.
Моментом инерции материальной точки относительно некоторой оси называется величина, равная произведению массы точки на квадрат ее расстояния от оси вращения
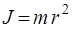 . (2)
. (2)
Для протяженных тел момент инерции определяется как сумма моментов инерции элементарных масс 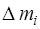 (материальных точек), на которые можно разбить тело:
(материальных точек), на которые можно разбить тело:
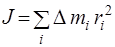 . (3)
. (3)
Имеются различные методы экспериментального определения моментов инерции. В настоящей работе определение моментов инерции тел произвольной формы производится методом колебаний. Для этих целей измеряется период колебаний Т математического и физического маятников.
Математическим маятником называется материальная точка массой m 0, подвешенная на невесомой, нерастяжимой нити и совершающая колебания под действием силы тяжести.
Момент инерции математического маятника
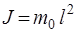 , (4)
, (4)
где l – длина маятника.
Период колебаний математического маятника определяется по формуле
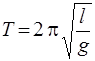 . (5)
. (5)
Физическим маятником называется твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси, не совпадающей с его центром инерции, под действием силы тяжести.
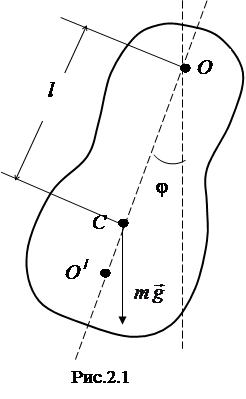 |
Если отклонить маятник от положения равновесия на угол φ (рис. 1), то момент силы, стремящийся вернуть маятник в положение равновесия равен
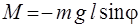 . (6)
. (6)
В (6) l – расстояние между точкой подвеса и центром инерции маятника С, m – масса маятника, 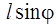 – плечо силы тяжести. Основное уравнение динамики вращательного движения (1) с учетом (6) можно записать в виде
– плечо силы тяжести. Основное уравнение динамики вращательного движения (1) с учетом (6) можно записать в виде
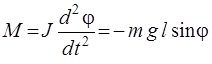 .
.
При малых углах отклонения 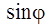 ~ φ, тогда
~ φ, тогда
 . (7)
. (7)
Уравнение (7) можно переписать в виде
 (8)
(8)
или
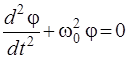 . (9)
. (9)
Решение этого уравнения имеет вид
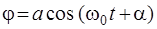 , (10)
, (10)
где а и α – произвольные постоянные. Через ω02 обозначена величина
ω02 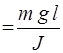 . (11)
. (11)
Из уравнений (9) и (10) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Зная ω0, можно рассчитать период колебания Т физического маятника:
ω0 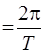 ,
, 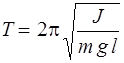 . (12)
. (12)
Из сопоставления формул (5) и (12) следует, что математический маятник длиной
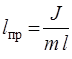 (13)
(13)
будет иметь такой же период колебаний, что и данный физический маятник. Величину 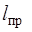 называют приведенной длиной физического маятника.
называют приведенной длиной физического маятника.
Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения О, называется центром качания физического маятника О /.
По теореме Штейнера момент инерции тела относительно любой оси
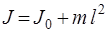 , (14)
, (14)
где 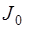 – момент инерции тела относительно оси, проходящей через центр тяжести, l – расстояние между осями.
– момент инерции тела относительно оси, проходящей через центр тяжести, l – расстояние между осями.
Подставим в уравнение (13) момент инерции, определяемый выражением (14):
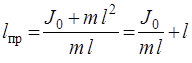 . (15)
. (15)
Из уравнения (15) видно, что приведенная длина всегда больше l, так что точка подвеса О и центр качания О / лежат по разные стороны от центра инерции С. Зная период колебания Т, массу маятника m и приведенную длину, можно рассчитать момент инерции J физического маятника:
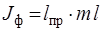 или
или 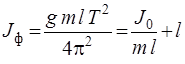 . (16)
. (16)
 2015-10-16
2015-10-16 1971
1971








