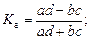Оценка тесноты линейной и нелинейной связи

Величина корреляционного отно- шения h	h = 0	0 < h < < 0,3	0,3 < h < < 0,6	0,6 < h < < 0,8	h > 0,8	h = 1
Теснота связи	Отсутствует	Слабая	Средняя	Выше средней	Сильная	Полная

ние называется корреляционным. Корреляционное отношение характеризует долю вариации результативного признака, вызванную действием факторного признака, положенного в основание группировки.

Для измерения тесноты связи одновременно трех признаков и более вычисляется множественный коэффициент корреляции. Он применяется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков.

Множественный коэффициент корреляции вычисляется по формуле

,

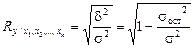где 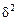– дисперсия теоретических значений результативного при-
знака, определенная по уравнению множественной рег-
рессии;

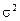– общая дисперсия результативного признака;

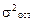– остаточная дисперсия.

Если необходимо оценить тесноту связи между результативным (y) и двумя факторными признаками (x ₁, x ₂), то применяется формула

,

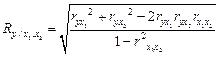где 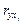– парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции положителен,
изменяется в пределах от 0 до 1. Приближение значения R
к единице свидетельствует о сильной зависимости между признаками.

Частные коэффициенты корреляции позволяют определить степень тесноты связи между результативным признаком y и каждым из факторных признаков при исключении влияния других факторных признаков.

Расчеты ведутся по формулам

; ,

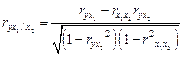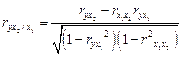где r – парные коэффициенты корреляции между указанными в ин-
дексе переменными.

При этом в первом случае исключено влияние факторного признака x ₂, а во втором – x ₁. Величина частных коэффициентов находится в пределах от 0 до 1.

При небольшом количестве данных может применяться простейший показатель тесноты связи – коэффициент Фехнера K _Ф (коэффициент корреляции знаков):

,

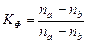где n_a , n_b – соответственно количество совпадений и несовпадений
отклонений величин факторного x и результативного y
признаков от их средних значений.

Таким образом, коэффициент Фехнера предполагает подсчет совпадений и несовпадений знаков отклонений индивидуальных значений каждого признака (x_i и y_i) от своей средней величины, т. е. 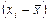и 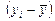. Тогда получают отношение разности числа пар совпадений и несовпадений знаков к их сумме, т. е.
к общему числу наблюдаемых единиц.

Если знаки всех отклонений по каждому признаку совпадут, то n_b = 0. В этом случае K _Ф = 1 (наличие прямой связи). Если знаки не совпадут, то n_a = 0. Тогда K _Ф = –1 (обратная связь). Если n_a = n_b, то K _Ф = 0.

Коэффициент Фехнера показывает наличие и направление связи. Он может принимать значения от –1 до +1. Чем ближе значение коэффициента к единице, тем сильнее связь между признаками.

Наличие корреляционной связи можно определить и для
качественных признаков с помощью специальных коэффи-
циентов.

10.6. Показатели тесноты связи
между качественными признаками

Важной задачей статистики является изучение социально-эко-
номических явлений, не имеющих количественной оценки. Количественная оценка связей таких явлений осуществляется с по-
мощью специальных показателей.

Для оценки тесноты связи между качественными признаками используются следующие показатели:

· коэффициенты ассоциации K _а и контингенции K _к;

· коэффициенты взаимной сопряженности Пирсона K _П и Чупрова K _Ч;

· модификации коэффициентов Пирсона и Чупрова;

· бисериальный коэффициент корреляции r.

Эти коэффициенты применяются для измерения тесноты связи между группировочными признаками в таблицах взаимной сопряженности.

Коэффициенты ассоциации и контингенции применяются для определения тесноты связи двух качественных признаков, каждый из которых является альтернативным (состоит только из двух групп). Для их вычисления строится таблица «четырех полей», содержащая частоты a, b, c и d двух альтернативных признаков A и B (табл. 10.5).

Расчеты ведутся по следующим формулам:

· коэффициент ассоциации:

· коэффициент контингенции:

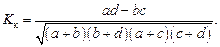
Значение коэффициента контингенции всегда меньше значения коэффициента ассоциации. Связь считается подтвержденной, если | K _а| > 0,5 или | K _к| > 0,3.

Таблица 10.5

Таблица для вычисления
коэффициентов ассоциации и контингенции

Признак	А (да)	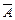(нет)	Итого
В (да)	a	b	a + b
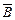(нет)	c	d	c + d
Итого	a + c	b + d	a + b + c + d

Если каждый из качественных признаков состоит более чем из двух групп, то теснота связи измеряется с помощью коэффициентов взаимной сопряженности Пирсона K _П и Чупрова K _Ч. Эти коэффициенты вычисляются по формулам

;

,

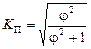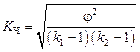где 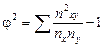– показатель взаимной сопряженности;

k ₁ – число значений (групп) первого признака;

k ₂ – число значений (групп) второго признака.

Коэффициенты изменяются в пределах от 0 до 1, направления связи не показывают. Чем ближе значения K _П и K _Ч к единице, тем теснее связь между качественными признаками. Коэффициент Чупрова более точен и всегда меньше, чем коэффициент Пирсона.

Для расчета коэффициента взаимной сопряженности используется специальная вспомогательная таблица (табл. 10.6).

Величину 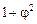преобразовывают следующим образом:

.

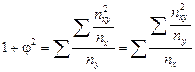Таблица 10.6

Вспомогательная таблица
для расчета коэффициента взаимной сопряженности

y x	I	II	III	Всего
I	…	…	nyx	nx
II	…	…	…	nx
III	…	…	…	nx
Итого	ny	ny	ny	n

Рассмотрим модификацию коэффициента Пирсона на основе расчета c²-критерия. Если ввести обозначение 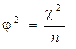, то получим формулу

,

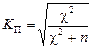где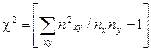

– наиболее распространенный критерий согласия (применяется для проверки статистической гипотезы о виде рас- пределения).

Рассмотрим модификацию коэффициента сопряженности Чупрова. В этом случае применяется формула вида

,

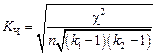где n – число наблюдений;

k ₁ – число строк в таблице;

k ₂ – число граф в таблице.

Для оценки связи между качественным альтернативным
и количественным варьирующим признаками применяется
бисериальный коэффициент корреляции:

,

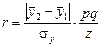где 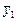и 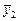– средние величины в группах;

s _y – среднее квадратическое отклонение фактических зна-
чений признака от его среднего уровня;

p – доля первой группы;

q – доля второй группы;

z – табличные значения Z -распределения в зависимости от
значений p.

Таким образом, использование показателей тесноты связи между качественными признаками способствует всестороннему изучению взаимосвязей между явлениями.