В соответствии с теорией естественной структуры ткани [8÷10] в начальный период времени после снятия с ткацкого станка (после снятия внешней нагрузки на ткань) происходит изменение формы нитей (распрямление одних и прогиб других) в результате самопроизвольного процесса минимизации уровня потенциальной энергии деформированных нитей до момента выравнивания сил взаимного давления. Только с этого момента можно считать процесс формирования структуры суровой ткани законченным в значительной степени, только тогда трансформация формы и взаимного расположения нитей, рельефность обеих поверхностей и толщина ткани позволят определить степень соответствия полученной ткани замыслу дизайнера.
На основе теоретических положений сопротивления материалов Писаренко [23], использованных при разработке теории естественной структуры ткани [8÷10], представим нить как статически неопределимую неразрезную балку на шарнирно-подвижных опорах с повторяющейся схемой нагрузки (Фиг.10), в которой величина прогиба hwp (hwft) участка каждой нити в элементе ткани зависит от расстояния между опорами Lwp (Lwft), силы давления Pwft (Pwp) со стороны нити другой системы, модулей упругости Ewft и Ewp, моментов инерции Jwft и Jwp, площадей поперечного сечения нити Fwft и Fwp и др. (здесь и далее обозначения наши).
Фиг.7
В соответствии с [23] балку (нить основы) на опорах на Фиг.10,а следует заменить эквивалентной системой (b) в виде отдельных двухопорных балок с приложением дополнительных изгибающих опорных моментов Хn-1, Xn и Xn+1 для учета влияния нагруженных соседних участков нити на рассматриваемый пролет балки Lwp. Величину и знак неизвестных опорных моментов можно определить с помощью уравнения трех моментов по способу Верещагина. Для этого на Фиг.10,с основная система представлена в виде отдельных, не связанных между собой балочек. На первом этапе необходимо провести построение эпюр Mbp (Фиг.10,d) только от заданной нагрузки Pwft. Затем следует определить площади эпюр Ωn и Ωn+1 и координаты аi и bi их центров тяжести. Упрощенное уравнение трех моментов (применительно к балке постоянного сечения J=Const) имеет вид:
Mn-1ℓn +2Mn(ℓn+ ℓn+1) + Mn+1ℓn+1 = -6(Ωnai / ℓn + Ωn+1bn+1 / ℓn+1) (27)
Это уравнение позволило определить величину и знак опорных моментов Мi:
Mn-1 = Mn = Mn+1 = - (1/8) PwftLwp (28)
Тогда полная реакция опоры n будет равна сумме реакций на действие двух соседних участков ℓn и ℓn+1
Rn = An + Bn = Pwft /2 + Pwft /2 = Pwft (29)
Для реальной балки (участка нити основы Lwp) выражения поперечных сил Q (Фиг.10,e) и изгибающих моментов Мb (Фиг.10,f) на удалении Х от опоры (n-1) будут иметь вид:
на участке Х1 : Q(х1) = Pwft/2; M(x1) = 0,5(PwftX1 – 0,25Pwft Lwp) (30)
на участке Х2: Q(х2) = -Pwft/2; M(x2) = 0,5(-PwftX2 + 0,75Pwft Lwp) (31)
Из равенства М(х1) = 0 определяется координата Хb точки перегиба осевой линии нити основы (Фиг.10,g):
Xb = Lwp/4 (32)
Применительно к текстильным материалам, особенностям их физических свойств наиболее полно можно описать действие внешней нагрузки и последующую разгрузку нитей в ткани законом сохранения энергии [23]. В соответствии с этим законом сначала упругое тело нити аккумулирует механическую энергию от действия рабочих органов ткацкого станка в виде накапливания потенциальной энергии деформации. Величина потенциальной энергии деформации численно равна работе внешних сил. Она не зависит от порядка нагружения, её величина полностью определяется конечными значениями усилий и перемещений.
После снятия с ткацкого станка потенциальная энергия проявляется в виде работы внутренних сил (сил упругости) при разгрузке (равной работе внешних сил) до момента достижения равновесного состояния элемента ткани.
Работа сил упругости нити основы (утка) Аwp (Awft), равная потенциальной энергии Uwp (Uwft) деформации изгиба, может быть определена из выражения [23]:
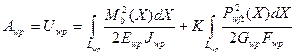 (33)
(33)
где Мb(Х) и Pwft (X) – изгибающий момент и поперечная сила давления нити утка в произвольном сечении нити основы;
Ewp, Gwp - модули упругости первого и второго рода для нити основы;
Jwp - осевой момент инерции;
Fwp - площадь поперечного сечения нити основы;
K - безразмерный коэффициент, зависящий от формы поперечного сечения нити.
Известно, что во всех структурах однослойных тканей 2D в результате взаимной деформации смятия нити приобретают эллипсовидную форму, поэтому численное значение коэффициента К применительно к эллипсу можно определить путем решения интегрального уравнения [23] вида:
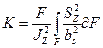 (34)
(34)
где F - площадь эллипса;
Jz - момент инерции всего поперечного сечения нити относительно оси изгиба Z;
Sz - статический момент отсеченной части эллипса относительно оси изгиба Z;
bs - ширина поперечного сечения нити на уровне определения касательных напряжений.
Для подстановки в формулу (34) принимаем: F= παb, bστ=2α, Jz= 0,25παb3.
Статический момент верхней половины поперечного эллипсовидного сечения нити относительно оси Z определим с ориентацией на Фиг. 11.
Фиг.11
Известно, что статический момент сечения равен произведению площади этого сечения на координату его центра тяжести
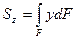 (35)
(35)
Для отсеченной части эллипса статический момент 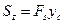
Уравнение линии контура площади эллипса
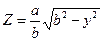 (36)
(36)
Площадь верхней отсеченной части можно выразить интегралом как функцией от нижнего предела
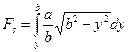 (37)
(37)
На элементарном участке площади эллипса dFi= Zdy приравняем ординаты yci ≈ y, где 0 ≤ y ≤ b.
Тогда ордината центра тяжести отсеченной части
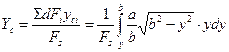 (38)
(38)
Статический момент рассматриваемой площади
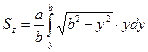 (39)
(39)
После подстановки b2 – y2 = X и замены пределов в результате решения интегрального уравнения получаем
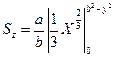 (40)
(40)
 В общем виде статический момент верхней отсеченной части относительно нейтрального слоя при изгибе нити будет иметь вид
В общем виде статический момент верхней отсеченной части относительно нейтрального слоя при изгибе нити будет иметь вид
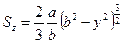 (41)
(41)
При максимальной площади отсекания (половины эллипса) y = 0, bs = 2α, dF = 2αdy
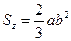 (42)
(42)
Интегральное выражение коэффициента К эллипсовидной формы поперечного сечения нити будет иметь вид
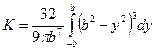 (43)
(43)
В результате после интегрирования получаем числовое значение безразмерного коэффициента для эллипсовидной формы нити
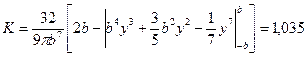 (44)
(44)
Величина прогиба нити в структуре ткани может быть определена общим методом Мора для статически неопределимых систем [23]. Учитывая только перемещения (прогиб), вызываемые изгибом по направлению i-i, интеграл Мора принимает вид:
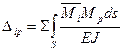
(45)
Где 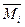 и Mp - изгибающие моменты в произвольном сечении вспомогательной и заданной систем;
и Mp - изгибающие моменты в произвольном сечении вспомогательной и заданной систем;
ds - длина элемента стержня.
Вычисление интеграла Мора можно упростить, если эпюра изгибающих моментов прямолинейна. Верещагин А.Н. предложил графоаналитический способ вычисления интеграла Мора [23] по формуле:
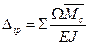 (46)
(46)
где Ω - площадь эпюры изгибающих моментов Mbp;
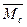 - ордината эпюры от единичной нагрузки под центром тяжести эпюры Mbp.
- ордината эпюры от единичной нагрузки под центром тяжести эпюры Mbp.
Без предварительного вычисления значений Uwp (Uwft) путем использования правила дифференцирования по параметру выражения (33) можно существенно упростить определение величины прогиба нити в ткани с помощью теоремы Кастильяно [23]: «Перемещение точки приложения обобщенной силы по направлению её действия равно частной производной от потенциальной энергии деформации по этой силе».
В итоге прогиб нити основы hwp под давлением уточной нити Pwft (при условии пренебрежения осевыми силами) можно определить по формуле:
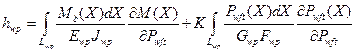 (47)
(47)
Прогиб уточной нити hwft определяется аналогично (47):
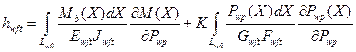 (48)
(48)
Для подстановки в формулы (47), (48) определим сначала частные производные изгибающих моментов Mb(X) и поперечных сил Q(X) в основной нити по силе давления уточины Pwft:
На первом участке
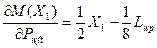 и
и 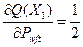 (49)
(49)
На втором участке
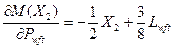 и
и 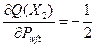 (50)
(50)
Для облегчения понимания определим прогиб нити основы hwp от силы давления уточины Pwft отдельно по слагаемым членам формулы (47) применительно к участкам Х1 и Х2.
На первом участке
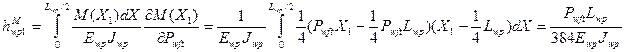 (51)
(51)
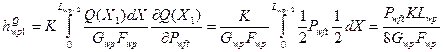 (52)
(52)
На втором участке
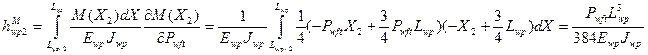 (53)
(53)
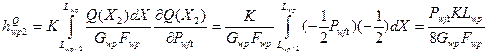 (54)
(54)
Суммарная величина слагаемых от действия изгибающих моментов будет равна
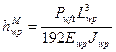 (55)
(55)
Суммарная величина слагаемых от действия поперечных сил будет равна
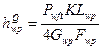 (56)
(56)
Полная величина прогиба нити основы в месте давления уточины может быть определена по выражению
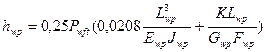 (57)
(57)
При полотняном переплетении полная величина прогиба уточной нити в месте давления нити основы определяется аналогичным выражением
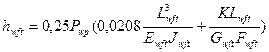 (58)
(58)
 2015-10-13
2015-10-13 392
392








