В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами (предикатами).
Пусть на множестве Х заданы две высказывательные формы А(х) и В(х).
Конъюнкцией высказывательных форм А(х) и В(х), заданных на множестве Х, называется высказывательная форма А(х)  В(х), заданная на том же множестве Х, истинная при тех значениях х
В(х), заданная на том же множестве Х, истинная при тех значениях х  Х, при которых обе формы А(х) и В(х) истинны одновременно.
Х, при которых обе формы А(х) и В(х) истинны одновременно.
Обозначение А(х)  В(х), читаем: «Конъюнкция А(х) и В(х)» или «А(х) и В(х)», т.е. так же, как и конъюнкция высказываний, конъюнкция высказывательных форм образуется с помощью союза «и».
В(х), читаем: «Конъюнкция А(х) и В(х)» или «А(х) и В(х)», т.е. так же, как и конъюнкция высказываний, конъюнкция высказывательных форм образуется с помощью союза «и».
Например, конъюнкцией высказывательных форм А(х): «х >2 и В(х): «х <5», х ÎN, является высказывательная форма А(х)  В(х): «х >2 и х <5», х ÎN, которую можно записать иначе: «2< x <5», х ÎN.
В(х): «х >2 и х <5», х ÎN, которую можно записать иначе: «2< x <5», х ÎN.
Таким образом, двойное неравенство а<x<в является конъюнкцией двух неравенств х>а и х<в.
Установим правило, которое позволит найти множество истинности конъюнкции высказывательных форм (предикатов), если известны множества истинности составляющих форм.
|
|
|
Рассмотрим пример.

 Пусть на множестве Х={1;2;3;4;5;6;7;8} даны высказывательные формы А(х): «х M2» и В(х): «х M3». Обозначим ТА и ТВ соответственно множества истинности высказывательных форм А(х) и В(х). Найдем ТА и ТВ: ТА = {2;4;6;8}, ТВ={3;6}. Теперь сформулируем конъюнкцию данных высказывательных форм: А(х)
Пусть на множестве Х={1;2;3;4;5;6;7;8} даны высказывательные формы А(х): «х M2» и В(х): «х M3». Обозначим ТА и ТВ соответственно множества истинности высказывательных форм А(х) и В(х). Найдем ТА и ТВ: ТА = {2;4;6;8}, ТВ={3;6}. Теперь сформулируем конъюнкцию данных высказывательных форм: А(х)  В(х): «х M2 и х M3», ее множеством истинности будет множество Т={6}. Очевидно, что множество Т является пересечением множеств ТА и ТВ: Т = ТА
В(х): «х M2 и х M3», ее множеством истинности будет множество Т={6}. Очевидно, что множество Т является пересечением множеств ТА и ТВ: Т = ТА  ТВ или Т АÙВ = ТА
ТВ или Т АÙВ = ТА  ТВ, где Т АÙВ – множество истинности А(х)
ТВ, где Т АÙВ – множество истинности А(х)  В(х). Множества истинности данных высказывательных форм и их конъюнкцию можно изобразить на диаграмме Эйлера-Венна (рис. 20).
В(х). Множества истинности данных высказывательных форм и их конъюнкцию можно изобразить на диаграмме Эйлера-Венна (рис. 20).
Х
TA TAÙB TB
Рис. 20
Таким образом, теперь можно сформулировать правило нахождения множества истинности конъюнкции высказывательных форм А(х)  В(х), х ÎХ, если известны множества истинности составляющих высказывательных форм А(х) и В(х), заданных на множестве Х.
В(х), х ÎХ, если известны множества истинности составляющих высказывательных форм А(х) и В(х), заданных на множестве Х.
Если ТА – множество истинности высказывательной формы (предиката) А(х), хÎХ, а ТВ – множество истинности высказывательной формы В(х), хÎХ, то множеством истинности Т А ÙВ высказывательной формы А(х)  В(х), хÎХ, является пересечение множеств истинности данных высказывательных форм А(х) и В(х), т.е. ТАÙВ = ТА
В(х), хÎХ, является пересечение множеств истинности данных высказывательных форм А(х) и В(х), т.е. ТАÙВ = ТА  ТВ.
ТВ.
Теперь рассмотрим понятие дизъюнкции высказывательных форм (предикатов).
Пусть на множестве Х заданы высказывательные формы А(х) и В(х).
Дизъюнкцией высказывательных форм А(х) и В(х), заданных на множестве Х, называется высказывательная форма А(х)  В(х), заданная на том же множестве, истинная при тех значениях х ÎХ, при которых истинна хотя бы одна из высказывательных форм А(х) и В(х).
В(х), заданная на том же множестве, истинная при тех значениях х ÎХ, при которых истинна хотя бы одна из высказывательных форм А(х) и В(х).
|
|
|
Обозначение А(х)  В(х), читаем: «Дизъюнкция А(х) и В(х)» или «А(х) или В(х)», т.е. по аналогии с дизъюнкцией высказываний дизъюнкция высказывательных форм образуется с помощью союза «или».
В(х), читаем: «Дизъюнкция А(х) и В(х)» или «А(х) или В(х)», т.е. по аналогии с дизъюнкцией высказываний дизъюнкция высказывательных форм образуется с помощью союза «или».
Например, дизъюнкцией высказывательных форм А(х): «х >5» и В(х): «х =5», х ÎN, является высказывательная форма А(х) 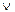 В(х): «х >5 или х =5», х ÎN, которую можно записать короче: «х ≥5», х ÎN.
В(х): «х >5 или х =5», х ÎN, которую можно записать короче: «х ≥5», х ÎN.
Таким образом, нестрогое неравенство вида х≥а (х≤а) является дизъюнкцией неравенства х>а (х<а) и равенства х=а.
Выведем правило, позволяющее найти множество истинности дизъюнкции высказывательных форм, если известны множества истинности составляющих форм.
Рассмотрим пример.
Пусть на множестве Х={1;2;3;4;5;6;7;8} даны высказывательные формы А(х): «х M2» и В(х): «х M3». Их множества истинности обозначим соответственно через ТА и ТВ; тогда ТА ={2;4;6;8}, ТВ={3;6}. Сформулируем дизъюнкцию данных высказывательных форм: А(х) 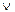 В(х): «х M2 или х M3», ее множество истинности обозначим ТА
В(х): «х M2 или х M3», ее множество истинности обозначим ТА  В, тогда ТА
В, тогда ТА  В = {2;3;4;6;8}. Нетрудно увидеть, что множество ТА
В = {2;3;4;6;8}. Нетрудно увидеть, что множество ТА  В является объединением множеств ТА и ТВ: Т А
В является объединением множеств ТА и ТВ: Т А  В =ТА
В =ТА  ТВ. Изобразим для наглядности множества истинности данных высказывательных форм и множество истинности дизъюнкции этих форм на диаграмме Эйлера-Венна (рис. 21), где ТА
ТВ. Изобразим для наглядности множества истинности данных высказывательных форм и множество истинности дизъюнкции этих форм на диаграмме Эйлера-Венна (рис. 21), где ТА  В - вся заштрихованная область.
В - вся заштрихованная область.


 Х
Х
TA TB
Рис. 21
Теперь сформулируем правило нахождения множества истинности дизъюнкции высказывательных форм А(х) 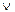 В(х), х Î Х, если известны множества истинности составляющих высказывательных форм А(х) и В(х), заданных на множестве Х.
В(х), х Î Х, если известны множества истинности составляющих высказывательных форм А(х) и В(х), заданных на множестве Х.
Если ТА - множество истинности высказывательной формы А(х), хÎХ, а ТВ - множество истинности высказывательной формы В(х), хÎХ, то множеством истинности ТА 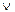 В высказывательной формы А(х)
В высказывательной формы А(х)  В(х), хÎХ, является объединение множеств истинности данных высказывательных форм А(х) и В(х), т.е. ТА
В(х), хÎХ, является объединение множеств истинности данных высказывательных форм А(х) и В(х), т.е. ТА 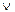 В = ТА
В = ТА  ТВ.
ТВ.
Выясним, как строить отрицание конъюнкции и дизъюнкции высказывательных форм А(х) и В(х), заданных на множестве Х. Используя законы де Моргана, рассмотренные и доказанные в пункте 2.3 настоящего пособия, а именно:  =`А
=`А  `B,
`B, 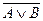 =`А
=`А  `B,сформулируем правило построения отрицания конъюнкции А(х) ÙВ(х) и дизъюнкции А(х)
`B,сформулируем правило построения отрицания конъюнкции А(х) ÙВ(х) и дизъюнкции А(х)  В(х) высказывательных форм, заданных на множестве Х.
В(х) высказывательных форм, заданных на множестве Х.
Чтобы построить отрицание конъюнкции А(х) Ù В(х) (дизъюнкции А(х)  В(х)) высказывательных форм А(х) и В(х), заданных на множестве Х, нужно заменить отрицаниями составляющие ее высказывательные формы, а союз «и» («или»)заменить союзом «или»(«и»), т.е. операцию конъюнкции (дизъюнкции) заменить операцией дизъюнкции (конъюнкции).
В(х)) высказывательных форм А(х) и В(х), заданных на множестве Х, нужно заменить отрицаниями составляющие ее высказывательные формы, а союз «и» («или»)заменить союзом «или»(«и»), т.е. операцию конъюнкции (дизъюнкции) заменить операцией дизъюнкции (конъюнкции).
Рассмотрим примеры образования отрицаний конъюнкции и дизъюнкции высказывательных форм.
1. Дана конъюнкция А(х) ÙB(х): «х M3 и х >5», х ÎN. Образуем ее отрицание: «Неверно, что х M3 и х >5» или, используя сформулированное выше правило, получим: «х не делится на 3 или х ≤5». Для множеств истинности ТА и ТВ высказывательных форм А(х) и В(х), заданных на множестве Х, при этом будет выполняться равенство:
Т¢АÙВ =Т¢А  Т¢В ,
Т¢В ,
т.е. дополнение множества истинности конъюнкции высказывательных форм А(х) и В(х) равно объединению дополнений к множествам истинности каждой высказывательной формы.
2. Для дизъюнкции А(х)  B(х): «х <2 или х – простое число», х ÎN, образуем отрицание: «Неверно, что х <2 или х – простое число» или, иначе, «х ≥2 и х – не простое число». Для множеств истинности ТА и ТВ высказывательных форм А(х) и В(х), заданных на множестве Х, будет выполняться равенство:
B(х): «х <2 или х – простое число», х ÎN, образуем отрицание: «Неверно, что х <2 или х – простое число» или, иначе, «х ≥2 и х – не простое число». Для множеств истинности ТА и ТВ высказывательных форм А(х) и В(х), заданных на множестве Х, будет выполняться равенство:
Т¢А 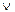 В=Т¢А
В=Т¢А  Т¢В,
Т¢В,
т.е. дополнение множества истинности дизъюнкции высказывательных форм А(х) и В(х) равно пересечению дополнений к множествам истинности каждой высказывательной формы.
|
|
|
 2015-10-22
2015-10-22 5891
5891








