Кривые второго порядка на плоскости

Определение 1. Геометрическое место точек (ГМТ), удовлетворяющих условию () (1) называется кривой второго порядка.

Что мы хотим выяснить по поводу кривых 2го порядка? Мы хотим узнать, какие бывают кривые второго порядка. Как изменить систему координат, чтобы уравнение этой кривой было записано максимально просто. Что означает поменять систему координат. Как меняется при этом уравнение кривой.

Пусть на плоскости задана декартова система координат, порожденная базисом , - взаимно перпендикулярных векторов единичной длины. В этой системе координат записано уравнение (1) кривой второго порядка.

Повернем базисные векторы на угол против часовой стрелки и получим новый базис , . Напишем разложение векторов нового базиса по старому базису: , . Пусть в старом базисе произвольный вектор представляется в виде и одновременно в новом базисе он равен . Выразив новые базисные векторы через старые, получим: . Т. к. разложение вектора по базису единственное, то Подставив эти выражения в уравнение (1), мы получим уравнение этой кривой 2-го порядка в новой системе координат . Если это уравнение записать в виде и несложно найти коэффициент .

Поставим перед собой такой вопрос. Можно ли повернуть систему координат таким образом, чтобы в новом уравнении кривой выполнялось условие , если первоначально ? Рассмотрим уравнение . Оно однородное и сводится к квадратному уравнению относительно тангенса после деления на квадрат косинуса: . Так как , то дискриминант этого квадратного относительно уравнения положителен и искомый поворот системы координат существует.

Итак, не теряя общности, можно считать, что наше уравнение кривой второго порядка записано в виде , при этом один из коэффициентов , отличен от 0. Пусть, например, , тогда и после замены «исчезает» соответствующий линейный член.

Перечислим те виды канонических уравнений, к которым после этих преобразований сведется уравнение (1). Уравнение 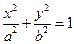(2) называется каноническим уравнением эллипса. Уравнение (3) называется каноническим уравнением гиперболы. Уравнение (4) называется каноническим уравнением параболы.

В остальных случаях говорят о вырожденных кривых второго порядка. Отметим уравнения: - мнимый эллипс, - точка, - пара прямых, - пара прямых, - прямая, - мнимая пара прямых.

С чем связаны названия: эллипс, гипербола, парабола?

Эллипс

Определение 2. Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.

Теорема 1. Пусть заданы числа и , такие что . Точками , сумма расстояний от которых до точек и равна , являются те и только те точки, координаты которых удовлетворяют уравнению (2), где .

Доказательство. Расстояние от точки до точки равно , расстояние от точки до точки равно . Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие . Перенесем второе слагаемое вправо и возведем обе части соотношения в квадрат, получив - равносильное уравнение. Отсюда или . Еще раз возведем обе неотрицательные части в квадрат и получим равносильное уравнение или . После деления на правую часть мы приходим к «нужному» уравнению 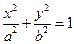, где . Теорема доказана.

В качестве характеристики эллипса (и других конических сечений – эллипса, гиперболы, параболы)) используется степень отклонения кривой от окружности – эксцентриситет, равный . Еще одной классической характеристикой является директриса – прямая, лежащая в плоскости конического сечения и такая, что отношение расстояний от любой точки кривой до соответствующего фокуса и до директрисы равно эксцентриситету. Для эллипса это две прямые .

Эллипс можно представить как единичную окружность, растянутую в раз вдоль оси абсцисс и в раз вдоль оси ординат.

Отметим, что уравнение эллипса может быть записано в параметрическом виде .

Гипербола

Определение 3. Гиперболой называется геометрическое место точек, разность расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.

Теорема 2. Пусть заданы числа и , такие что . Точками , разность расстояний от которых до точек и равна , являются те и только те точки, координаты которых удовлетворяют уравнению (3), где .

Доказательство. Расстояние от точки до точки равно , расстояние от точки до точки равно . Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие . Перенесем второе слагаемое вправо и возведем обе части соотношения в квадрат, получив - равносильное уравнение. Отсюда или . Еще раз возведем обе неотрицательные части в квадрат и получим равносильное уравнение или . После деления на правую часть мы приходим к «нужному» уравнению , где . Теорема доказана.

В качестве характеристики гиперболы рассматривают эксцентриситет, равный и директриса. Для гиперболы это две прямые .

У канонической гиперболы есть две асимптоты , т. е. прямые, к которым график функции неограниченно приближается при удалении от начала координат к бесконечности.

Отметим, что уравнение гиперболы может быть записано в параметрическом виде .

Парабола

Определение 4. Параболой называется геометрическое место точек, расстояние от который до заданной точки, называемой фокусом равно расстоянию до заданной прямой, называемой директрисой.

Теорема 2. Пусть задано число . Точками , расстояние от которых до точки равно расстоянию до прямой являются те и только те точки, координаты которых удовлетворяют уравнению (4).

Доказательство. Расстояние от точки до точки равно , расстояние от точки до прямой равно . Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие . Возведем обе части соотношения в квадрат и получим или . Теорема доказана.

У параболы эксцентриситет равен .