Приклади розв’язання типових задач

Задача 1. Нехай – зв’язний граф і – деяке його ребро. Позначимо через граф, який отримано з вилученням ребра . Довести, що:

a) граф є зв’язним, якщо ребро належить циклу в графі ;

b) граф є незв’язним і має рівно дві компоненти зв’язності, якщо ребро не входить у жодний цикл графа .

Розв’язання.

a) Нехай дві довільні вершини і є зв’язаними у графі . Покажемо, що вони будуть зв’язаними і у . Можливі два випадки. Якщо маршрут 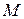, що з’єднує і у зв’язному графі , не містить ребро , то вилучення цього ребра не змінить зв’язності і у графі . Якщо ж ребро належить маршруту 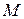і , то маршрут, що веде з у у графі , можна побудувати таким чином:

· беремо маршрут, що веде з в ;

· додаємо до нього ту частину циклу, що містив ребро , яка залишилась у графі та з’єднуємо вершини і ;

· беремо маршрут, що веде з в .

Отже, побудовано “обхідний” маршрут з до . Тому граф є зв’язним.

b) Нехай ребро не належить жодному циклу графа . Тоді у графі вершини та будуть незв’язаними і будуть належати двом різним компонентам зв’язності та графа . Крім того, у графі стануть незв’язаними ті і тільки ті вершини, які були з’єднані у графі маршрутом, що містив ребро . Отже, кожна вершина у буде зв’язаною або з вершиною , або з вершиною , тобто належатиме або , або . Це і означає, що має рівно дві компоненти зв’язності.

Задача 2. Якщо у простому графі тільки дві вершини та мають непарні степені, то вони зв’язані. Довести.

Розв’язання. Якщо граф зв’язний, то твердження очевидне. Нехай граф – незв’язний і вершина належить компоненті зв’язності . За наслідком з леми про рукостискання кожен простий граф має парну кількість вершин непарної степені. Тому і вершина повинна належати цій же компоненті, оскільки за умовою інших вершин непарної степені не існує. Отже, вершини та зв’язані.

Задача 3. Довести, що графи та ізоморфні.

Розв’язання. Побудуємо бієктивне відображення , що зберігає суміжність вершин в графах та :

.

При побудові відображення враховуємо степінь вершин графів: в графі існує одна вершина степені 4: . У графі теж існує лише одна вершина степені 4, отже, . У графі вершина 1 суміжна з вершинами 2 та 5, які мають степінь 2. У графі їм відповідають вершини та , отже, можна покласти та , і т.д.

Потрібно перевірити, що побудоване відображення дійсно зберігає суміжність вершин. Випишемо множину ребер графа :

.

Побудуємо множину :

.

Очевидно, що , тобто, якщо вершини та є суміжними у графі , то їх образи та є суміжними у графі . Отже, графи та ізоморфні.

Зауважимо, що відображення можна побудувати не єдиним чином. Наприклад, . Легко перевірити, що це відображення також зберігає суміжність вершин.

Задача 4. Нехай – ациклічний граф, і . Довести, що граф 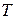є деревом.

Розв’язання. Дерево – це зв’язний ациклічний граф. Отже, потрібно довести, що 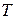– це зв’язний граф. Доведення проведемо від супротивного. Нехай 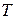– незв’язний граф, який має компонент зв’язності: , причому . Тоді кожен з графів є деревом. Нехай . Тоді . Просумувавши по всіх значеннях , маємо: або . Врахувавши, що за умовою , маємо . Отримали протиріччя припущенню . Отже, граф 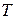має лише одну компоненту зв’язності, тобто є зв’язним. Це і означає, що граф Е є деревом.

A7

1. Побудувати діаграму, матрицю суміжності та інцидентності графа , де , .

2. Нехай задано матрицю суміжності деякого графа . Як за допомогою матриці визначити:

a) кількість вершин графа ;

b) кількість ребер графа ;

c) степінь певної вершини графа ;

d) чи має граф петлі;

e) чи є повним графом.

3. Побудувати діаграму повного графа з вершинами для:

а) ; b) ; c) ; d) ; e) ; f) .

4. Скільки ребер має повний граф з вершинами?

5. Побудувати декілька підграфів графа та декілька його остовних підграфів.

6. Скільки ребер у графі з вершинами, якщо кожна його вершина має степінь 2?

7. Чи існує граф із вершинами, усі вершини якого є кінцевими, якщо:

a) ; b) ?

8. Побудувати доповнення наведених графів:

a)

9. У певному товаристві з осіб кожен знайомий з і тільки іншими особами. Чи можливе таке товариство для:

a) ; b) ; c) ; d) ?

10. Нехай графи і задано за допомогою матриць суміжності і відповідно, . Визначити матрицю суміжності для графа:

a) ; b) ; c) ; d) .

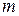11. Чому дорівнює степінь вершини у графі , якщо у графі з вершинами:

a) ; b) ; c) ; d) ?

12. Нехай задано граф :

Чи буде послідовність вершин 1 2 1 5 2 4 маршрутом? Побудувати:

a) маршрут, який з’єднує вершини 1 та 4 і не є ланцюгом;

b) ланцюг, який з’єднує вершини 1 та 4 і не є простим ланцюгом;

c) прості ланцюги, які з’єднують вершини 1 та 4 і мають найбільшу та найменшу довжини;

d) циклічний маршрут, який містить вершину 1 та не є циклом;

e) цикл, який містить вершину 1 та не є простим циклом;

f) прості цикли, які містять вершину 1 та мають найбільшу та найменшу довжини.

13. Нехай задано граф :

Знайти всі ланцюги, які з’єднують вершини 1 та 9. Скільки серед них буде простих?

14. Довести, що граф ізоморфний графу та граф ізоморфний графу . Показати, що граф ізоморфний графу .

15. Граф, ізоморфний своєму доповненню, називається самодоповнювальним графом. Довести, що існує тільки один самодоповнювальний граф із чотирма вершинами. Побудувати його.

16. Довести, що кількість вершин будь-якого самодоповнювального графа дорівнює або , або .

17. Довести, що для будь-якого графа він сам або його доповнення є зв’язним графом.

18. Побудувати всі дерева з п’ятьма вершинами (з точністю до ізоморфізму).

19. Незв’язний граф, кожна компонента зв’язності якого є дерево, називається лісом. Скільки ребер містить такий граф з вершинами і компонентами зв’язності?

20. Довести, що будь-яке дерево з вершинами () має принаймні дві кінцеві вершини.

21. Для графів та побудувати відповідні їм остовні дерева:

a) вилучаючи ребро з кожного циклу;

b) пошуком в ширину;

c) пошуком в глибину.

22. Скільки ребер потрібно вилучити зі зв’язного графа з вершинами та 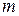ребрами, щоб отримати остовне дерево?

23. Нехай граф задано за допомогою матриці суміжності . Побудувати діаграму графа та його матрицю інцидентності, якщо

.

Знайти напівстепені входу і виходу кожної вершини. Зясувати, чи має цей граф джерело та стік.

24. Побудувати орієнтований граф з сімома вершинами, який має 2 недосяжні і 3 тупикові вершини.

B7

1. Побудувати діаграму, матрицю суміжності та інцидентності графа де , .

2. Нехай граф задано за допомогою матриці суміжності , граф – за допомогою матриці інцидентності . Побудувати діаграми цих графів, якщо

.

3. Побудувати всі графи з чотирма вершинами і 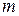ребрами

4. Чи існує повний граф, у якого кількість ребер дорівнює:

a) 15; b) 18; c) ?

5. Чи існує граф із шістьма вершинами, степені яких дорівнюють:

a) 1, 2, 3, 3, 4, 4; b) 2, 3, 3, 4, 4, 4; c) 2, 2, 2, 4, 5, 5.

Відповідь обґрунтувати.

6. Побудувати граф із п’ятьма вершинами, у якому тільки дві вершини мають однакові степені. Чи можуть ці вершини мати степінь 0 або степінь 4?

7. Побудувати об’єднання, перетин, різницю та доповнення графів:

8. Нехай задано два графи та :

Вилучити з графа :

a) вершину ; b) вершину ; c) ребро .

Вилучити з графа вершину .

9. Нехай задано граф :

a) Вказати степінь кожної вершини.

b) Перевірити лему про рукостискання та її наслідок.

c) Не будуючи доповнення , вказати, скільки ребер буде мати граф .

d) Чому дорівнюватимуть степені вершин 3 та 5 у графі ?

10. Нехай у графі з вершинами і 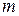ребрами є вершин степеня , а всі інші вершини мають степінь . Довести, що .

11. Кубічний граф – це граф, степінь кожної вершини якого дорівнює 3. Побудувати кубічний граф, що має:

a) 4 вершини; b) 6 вершин; c) 8 вершин.

Чи існує кубічний граф з вершинами, якщо:

а) b) ?

12. Скільки вершин повинен мати кубічний граф? Скільки ребер у такому графі?

13. Довести, що доповнення кубічного графа не є кубічним графом.

14. Чому дорівнює кількість ребер у графі , якщо граф має вершин і ребер?

15. Чи існує самодоповнювальний граф, у якого кількість ребер дорівнює: a) ; b) ?

16. Побудувати всі самодоповнювальні графи із п’ятьма вершинами.

17. Нехай задано граф :

Які з наведених нижче послідовностей вершин є маршрутом:

a) ; b) ; c) ; d) ?

Вказати ланцюги, прості ланцюги та довжину кожного маршруту.

18. Чи має граф

a) маршрут довжиною 5;

b) ланцюг довжиною 5;

c) простий ланцюг довжиною 5.

Навести приклади.

19. Якщо два різні цикли графа містять ребро , то в графі існує цикл, серед ребер якого немає ребра . Довести.

20. Побудувати всі дерева з 6 вершинами (з точністю до ізоморфізму).

21. Довести, що в дереві з вершинами виконується рівність , де степінь вершини .

22. Яку найбільшу і найменшу кількості кінцевих вершин може мати дерево з вершинами? Яку структуру мають такі дерева?

23. Описати всі дерева, доповнення яких також є деревами.

24. Описати всі дерева, які є самодоповнювальними графами.

25. Скільки основних дерев має повний граф ?

26. Побудувати орієнтований граф, який має 8 вершин, 2 стоки та одне джерело.

27. Побудувати повний орієнтований граф з шістьма вершинами.

C7

1. Нехай – матриця суміжності графа з вершинами. Довести, що -й діагональний елемент матриці дорівнює степеню -ї вершини графа .

2. Навести приклад графа, в якому існує простий ланцюг з вершини в вершину та з вершини у вершину , але не існує простого ланцюга з вершини у вершину через вершину .

3. Довести, що якщо зі зв’язного графа видалити довільне ребро, що міститься в деякому простому циклі, то граф залишиться зв’язним.

4. Довести, що в зв’язному графі будь-які два прості ланцюги максимальної довжини мають принаймні одну спільну вершину.

5. Задача Рамсея. Довести, що серед довільних шести осіб знайдуться або троє попарно знайомих, або троє попарно незнайомих.

6. З’ясувати, чи будуть ізоморфними графи:

a)

b)

c)

d)

9. Довести, що в графі з вершинами, який має більше ніж ребро, є принаймні один цикл.

10. Описати у термінах теорії графів наступні бінарні відношення на скінченній множині: a) транзитивні відношення; b) відношення еквівалентності; c) відношення часткового порядку; d) відношення лінійного порядку.

11. Описати відношення, що відповідають: a) орієнтованим графам без петель; b) неорієнтованим графам без петель; c) орієнтованим графам з петлями.