Математическое ожидание

Кроме закона распределения, который дает полное представление о случайной величине, часто используют числа, которые описывают случайную величину суммарно. Такие числа называют числовыми характеристиками случайной величины. Среди числовых характеристик важным является математическое ожидание, которое указывает, какое среднее значение случайной величины следует ожидать в результате испытания или наблюдения.

Определение 4. Математическим ожиданием или средним значением М(Х) дискретной случайной величины Х называется сумма произведения всех её возможных значений х_i на их вероятности р_i,т.е. М(Х) = х₁р₁ + х₂р_{2 + … +}x_np_n = .

Определение 5. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых величин равны их безусловным распределениям.

Свойства: 1. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = СМ(Х)

2. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: М(Х + У) = М(Х) + М(У)

3. Математическое ожидание постоянной величины С равно самой этой величине С, М(С) = С

4. Математическое ожидание линейной комбинации случайной величины равно линейной комбинации их математических ожиданий: М

5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: М(ХУ) = М(Х) · М(У)

Пример 12. Найдите математическое ожидание случайной величины Х по закону ее распределения

Х	- 1
р	0,2	0,1	0,25	0,15	0,3

Решение: По формуле М(Х) = х₁р₁ + х₂р_{2 + … +}x_np_n = . находим М(Х) = - 1 · 0,2 + + 0 · 0,1 + 1 · 0,25 + 2 · 0,15 + 3 · 0,3 = 1,25.

2. Дисперсия. Дисперсия случайной величины характеризует степень разброса, рассеивание случайной величины лтносительноеё математического ожидания (среднего значения). Само слово «дисперсия» означает «рассеивание».

Определение 6. Отклонением называется разность между случайной величиной Х и ее математическим ожиданием М(Х), т. е. Х – М(Х).

Замечание: Отклонение Х – М(Х) и его квадрат (Х – М(Х))² являются случайными величинами.

Определение 7. Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата ее отклонения:

D(X) = M(X – M(X))² = M(X)² – (M(X))²

Свойства: 1. Дисперсия постоянной величины равна 0: D(C) = 0

2. Если Х – случайная величина, а С – постоянная, то

а) D(CX) = C²D(X)

б) D(X + C) = D(X)

3. Дисперсия от суммы случайных независимых величин равна сумме дисперсий случайных независимых величин: D(X + Y) = D(X) + D(Y)

3. Среднее квадратное отклонение случайной величины.

Определение 8. Средним квадратным отклонением случайной величины называется корень квадратный из её дисперсии:

Пример 13. Дискретная случайная величина распределина по закону:

Х	- 1
Р	0,2	0,1	0,3	0,4

Найдите дисперсию случайной величины и среднее квадратное отклонение.

Решение: 1) Находим М(Х) по фрмуле: М(Х) = х₁р₁ + х₂р_{2 + …}₊x_np_n = .

М(Х) = - 1 · 0,2 + 0· 0,1 + 1· 0,3 + 2 · 0,4 = 0,9

2) M(X²) = (- 1)² · 0.2 + 0² · 0.1 + 1² · 0.3 + 2² · 0.4 = 2.1

3) Находим D(X) по формуле: D(X) = M(X)² – (M(X))². D(X) = 2,1 – (0,9)² = 1,29

4) Находим . = 1,136

Элементы математической статистики

Предмет математической статистики. Исходным материалом для любого статистического исследования являются статистические данные. Под статистическими данными понимаются сведения о числе объектов, какой-либо обширной совокупности, обладающих теми или иными признаками (число студентов, родившихся в 1980 г.).

На основании статистических данных можно сделать определенные научно-обоснованные выводы. Для этого статистические данные должны быть предварительно определенным образом систематизированы и обработаны.

Одним из основных методов обработки статистических данных является выборочный метод.

Выборочный метод. При выборочном исследовании из всей совокупности отбирают некоторым образом определенное число объектов и только их подвергают исследованию. Совокупность всех исследуемых объектов называют генеральной совокупностью. Выборкой называют совокупность случайно отобранных объектов из генеральной совокупности. Число объектов выборки или генеральной совокупности называют объемом выборки (из 500 студентов для контрольной флюорографии отобрано 50 студентов, то объем генеральной совокупности равен 500, а объем выборки равен 50). Разность между наибольшим и наименьшим значением числовой выборки называют размахом выборки.

Выборку, представляющую собой неубывающую последовательность чисел, называют вариационным рядом. Любую числовую выборку можно записать в виде вариационного ряда.

Пример 66. Найти вариационный ряд, объем выборки и размах у следующей выборки: 1, 10, -2, 0, -2, 5, 1, 10, 7.

Решение:

Вариационный ряд: -2, -2, 0, 1, 1, 5, 7, 10, 10.

Объем выборки:

Размах:

Пусть из генеральной совокупности получена выборка объема 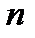, причем появляется в ней раз, значение - раз и т.д. в этом случае числа , , …, называют частотами значения выборки. Отношения , , …, называют относительными частотами значения выборки.

Последовательность пар (, ), (, ), …, (, ) называют статистическим рядом. Обычно статистический ряд записывают в виде таблицы, где - значения выборки, а 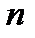- частоты значения выборки.

		…
		…

Выборочное распределение записывается в виде таблицы, где - значения выборки, а - относительные частоты выборки.

		…
		…

Пример 67. Дана выборка 3, 8, -1, 3, 0, 5, 3, -1, 3, 5. Записать статистический ряд и выборочное распределение.

Решение. Запишем данную выборку в виде вариационного ряда: -1, -1, 0, 3, 3, 3, 3, 5, 5, 8.

Статистический ряд будет иметь следующий вид:

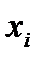
	-1

Выборочное распределение:

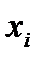
	-1
	0,2	0,1	0,4	0,2	0,1

Графическое изображение выборки. Полигон и гистограмма. Для наглядного представления выборки часто используют различные графические изображения. Простейшим графическим изображением выборки являются полигон частот (выборки). Пусть выборка задана статистическим рядом (, ), (, ), …, (, ). Полигоном частот (выборки) называется ломаная линия. Существует два вида полигонов выборки: полигон частот и полигон относительных частот (рис. 19).

Рисунок 19.

Пример 68. Задано распределение частот выборки объема .

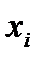
Написать распределение относительных частот; построить полигон относительных частот.

Решение. Найдем относительные частоты

, .

Проверка:

Напишем распределение относительных частот:


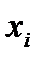
	0,15	0,5	0,35

В системе прямоугольных координат строим полигон относительных частот (рис. 20).

рисунок 20.

Упражнения для самопроверки

1. а) В урне 3 белых шара и 9 черных шаров. Из урны наугад вынимают один шар. Какова вероятность того, что вынутый шар окажется черным?

б) В урне 4 красных шара и 7 синих шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара красные?

в) Первенство по футболу оспаривают 18 команд, среди которых 5 лидирующих. Путем жеребьевки команды распределены на две группы по 9 команд в каждой. Какова вероятность попадания всех лидирующих команд в одну группу?

2. Построить полигон по данному распределению выборки

а)

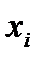
б)

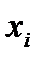
Ответы. 1. а) 3/4; б) 6/55; в) 1/3

задание на Контрольную работу № 1

Контрольная работа составлена в 50 вариантах. Вариант контрольной работы определяется двумя последними цифрами шифра студента по таблице вариантов контрольной работы.

Таблица вариантов контрольной работы № 1