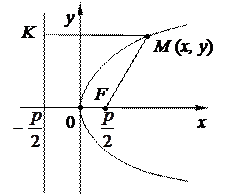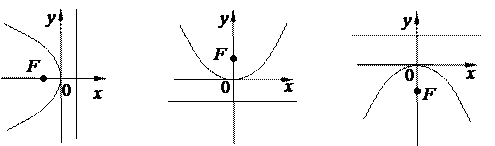Министерство образования и науки Российской Федерации
Волгоградский государственный архитектурно-строительный университет
Кафедра высшей математики
Линейная алгебра и аналитическая геометрия
На плоскости и в пространстве
Методические указания и индивидуальные задания
К контрольной работе №1
Волгоград 2011
УДК 512.64+514.12(076.5)
Линейная алгебра и аналитическая геометрия на плоскости
и в пространстве: Методические указания и индивидуальные задания
к контрольной работе №1 / Сост. Н.А. Болотина, К.В. Катеринин, Р.К. Катеринина, И.П. Руденок; Волгогр. гос. архит. - строит. ун-т. — Волгоград: ВолгГАСУ, 2011. — 22 c.
Содержатся краткие теоретические сведения, решения типовых примеров, индивидуальные задания.
Для студентов сокращенной формы обучения ИДО всех специальностей техники и технологии по дисциплине "Математика".
Библиогр. назв. 3
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
И РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
1. Определители
|
|
|
1.1. Основные определения
Определителем второго порядка называется число, обозначаемое символом  или Δ и определяемое равенством:
или Δ и определяемое равенством:
 . (1)
. (1)
Определителем третьего порядка называется число, обозначаемое символом  или Δ и определяемое равенством:
или Δ и определяемое равенством:
 . (2)
. (2)
Определители второго порядка, входящие в правую часть равенства (2), получаются из данного определителя третьего порядка вычёркиванием одной строки и одного столбца, на пересечении которых стоят элементы a 1, b 1, c 1. Формула (2) называется формулой разложения определителя по элементам первой строки.
Пример 1. Вычислить определитель Δ=  .
.
Решение. По формулам (2) и (1) получим:
 .
.
1.2. Решение невырожденных систем линейных алгебраических уравнений по формулам Крамера
Определителем системы трёх линейных уравнений с тремя неизвестными x, y и z
 (3)
(3)
называется определитель  .
.
Определители Δ x = 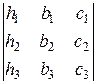 , Δ y =
, Δ y =  , Δ z =
, Δ z = 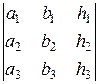
называются дополнительными определителями.
Если определитель системы Δ отличен от нуля, то система называется невырожденной и имеет единственное решение, которое может быть найдено по формулам Крамера:
 (4)
(4)
Пример 2. Решить систему уравнений: 
Решение. Найдём определитель системы: Δ=  =18.
=18.
Так как Δ≠ 0, то решение данной системы можно найти по формулам Крамера. Для этого вычислим дополнительные определители:
Δ x =  =18, Δ y =
=18, Δ y =  =0, Δ z =
=0, Δ z =  =-36.
=-36.
Теперь по формулам (4) получим:

2. Элементы векторной алгебры
2.1. Основные определения
Вектором называется отрезок, имеющий определённую длину и направление. Вектор обозначается или указанием его начала и конца  (точка А — начало, В — конец вектора), или одной буквой, например,
(точка А — начало, В — конец вектора), или одной буквой, например, 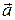 .
.
|
|
|
Длина вектора, называемая также модулем, обозначается  или
или  .
.
Коллинеарные векторы лежат на одной или параллельных прямых, компланарные — на одной или параллельных плоскостях.
Взаимно противоположные векторы равны по длине и противоположны по направлению. Векторы, противоположные векторам  и
и 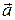 обозначают
обозначают 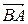 и
и  .
.
Вектор, модуль которого равен 1, называется единичным.
Единичный вектор, направление которого совпадает с направлением вектора 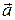 , называется ортом этого направления и обозначается
, называется ортом этого направления и обозначается  .
.
Вектор 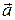 можно представить в виде
можно представить в виде  .
.
Орты, имеющие направление прямоугольных координатных осей Ох, Оу, Оz обозначаются соответственно  .
.
Каждый вектор 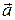 может быть единственным образом разложен на сумму векторов, параллельных ортам
может быть единственным образом разложен на сумму векторов, параллельных ортам  :
:
 . (5)
. (5)
Числа х, Y, z называются прямоугольными декартовыми координатами вектора 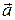 и являются его проекциями на соответствующие координатные оси.
и являются его проекциями на соответствующие координатные оси.
Равенство (5) может быть записано в виде  или
или  .
.
Если заданы точки 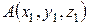 и
и  , то координаты вектора
, то координаты вектора  находятся по формулам:
находятся по формулам:
Х = х 2 -х 1, Y = y 2 -y 1, Z = z 2 -z 1, (6)
а его длина равна
 =
= 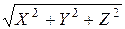 =
=  . (7)
. (7)
Используя формулу (7) можно найти расстояние между точками 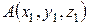 и
и  :
:
 . (8)
. (8)
2.2. Скалярное произведение
Скалярным произведением векторов 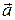 и
и  называется число, обозначаемое
называется число, обозначаемое  и равное произведению длин этих векторов на косинус угла между ними:
и равное произведению длин этих векторов на косинус угла между ними:
 =
=  , (9)
, (9)
где 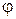 — угол между векторами
— угол между векторами 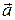 и
и  (рис.1).
(рис.1).

Рис.1
Скалярное произведение векторов  и
и  вычисляется по формуле
вычисляется по формуле
 =
=  , (10)
, (10)
а угол между ними — по формуле
 (11)
(11)
2.3. Векторное произведение
Векторным произведением вектора 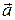 на вектор
на вектор  называется вектор, обозначаемый
называется вектор, обозначаемый 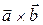 , который удовлетворяет трем требованиям:
, который удовлетворяет трем требованиям:
– перпендикулярен каждому из векторов 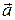 и
и  ;
;
– имеет длину, равную  , где
, где 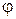 – угол между векторами;
– угол между векторами;
– направлен так, чтобы кратчайший поворот от 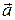 к
к  , если смотреть из конца вектора
, если смотреть из конца вектора  , совершался против часовой стрелки (рис.2).
, совершался против часовой стрелки (рис.2).

Рис.2
Так как площадь параллелограмма, построенного на векторах 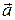 и
и 
и длина вектора 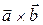 равны одному и тому же числу
равны одному и тому же числу  , то для вычисления площади параллелограмма можно пользоваться формулой:
, то для вычисления площади параллелограмма можно пользоваться формулой:
 .
.
Тогда площадь треугольника, построенного на этих векторах, равна:
 . (12)
. (12)
Если векторы 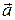 и
и  заданы своими координатами
заданы своими координатами  и
и  , то векторное произведение определяется формулой
, то векторное произведение определяется формулой
 . (13)
. (13)
4.Смешанное произведение.
Смешанным или векторно-скалярным произведением трёх векторов
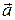 ,
,  и
и  называется число, которое получится, если векторы
называется число, которое получится, если векторы 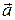 и
и  перемножить векторно, а полученный вектор
перемножить векторно, а полученный вектор 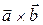 умножить скалярно на вектор
умножить скалярно на вектор  . Смешанное произведение обозначается
. Смешанное произведение обозначается  .
.
Геометрически смешанное произведение векторов 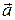 ,
,  ,
,  есть число, абсолютная величина которого равна объёму V параллелепипеда, построенного на этих векторах как на рёбрах, то есть
есть число, абсолютная величина которого равна объёму V параллелепипеда, построенного на этих векторах как на рёбрах, то есть
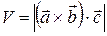 .
.
Объём треугольной пирамиды, построенной на векторах 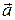 ,
,  ,
,  , вычисляется по формуле:
, вычисляется по формуле:
 . (14)
. (14)
Если векторы  ,
,  и
и  заданы координатами, то их смешанное произведение равно:
заданы координатами, то их смешанное произведение равно:
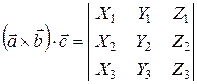 . (15)
. (15)
Пример 3. Даны координаты вершин пирамиды А 1 (1; 2; 3), А 2 (-2; 4; 1), А 3 (7; 6; 3), А 4 (4; -3; -1). Требуется найти:
1) координаты и модули векторов  и
и  ;
;
2) угол между рёбрами 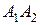 и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды.
Решение. 1) Координаты векторов  и
и  найдём по формуле (6):
найдём по формуле (6):
 =(-2–1; 4–2; 1–3)=(-3; 2; -2).
=(-2–1; 4–2; 1–3)=(-3; 2; -2).
 =(4–1; -3–2; -1–3)=(3; -5; -4).
=(4–1; -3–2; -1–3)=(3; -5; -4).
Модули векторов вычислим по формуле (7):
 ,
,  .
.
2) Угол между рёбрами  и
и  найдём как угол между соответствующими векторами по формуле (11):
найдём как угол между соответствующими векторами по формуле (11):

В числителе стоит скалярное произведение векторов, по формуле (10) оно равно  ·
·  = (-3)·3+2·(-5)+(-2)·(-4)=-9 -10+8=-11.
= (-3)·3+2·(-5)+(-2)·(-4)=-9 -10+8=-11.
Теперь находим

3) Площадь грани  найдём как площадь треугольника, построенного на векторах
найдём как площадь треугольника, построенного на векторах  и
и  по формуле (12):
по формуле (12):

Для этого сначала определим координаты вектора  :
:
 =(7–1; 6–2; 3–3)=(6; 4; 0).
=(7–1; 6–2; 3–3)=(6; 4; 0).
Векторное произведение  ×
×  найдем по формуле (13):
найдем по формуле (13):

Длина этого вектора равна:

Площадь грани  равна:
равна:

4) Данная пирамида построена на векторах  ,
,  и
и  , поэтому её объём найдем по формуле (14):
, поэтому её объём найдем по формуле (14):
|
|
|

Сначала вычислим смешанное произведение

Потом найдём 
3. Аналитическая геометрия на плоскости
3.1. Прямая на плоскости. Различные уравнения
В прямоугольной системе координат Оху уравнение первой степени относительно переменных х и у
Ах + Ву + С =0 (16)
определяет некоторую прямую (коэффициенты А и В не равны нулю одновременно). Здесь х и у — координаты любой точки, лежащей на этой прямой. Уравнение (16) называется общим уравнением прямой.
Уравнение всякой прямой, не параллельной оси Оу, может быть представлено в виде
у = kx + b, (17)
где k = tg α — угловой коэффициент прямой, α — угол наклона прямой к оси Ох (рис.3), b — отрезок, отсекаемый прямой от оси Оу (с учётом знака).


Рис. 3
Уравнение (17) называется уравнением прямой с угловым коэффициентом.
Уравнение прямой, проходящей через заданную точку М0 (х0, у0) в заданном направлении (известен угловой коэффициент) имеет вид
у – у0 = k (х–х0). (18)
Если известны две точки М 1(х 1, у 1) и М 2(х 2, у 2), то прямая, проходящая через эти точки, определяется уравнением
 .(19)
.(19)
Расстояние d от точки М0 (х0, у0) до прямой Ах + Ву + С =0 находится по формуле
 (20)
(20)
3.2. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
Если известны угловые коэффициенты k 1 и k 2 прямых, то угол φ между этими прямыми (рис.4) определяется по формуле
 j =
j = 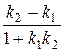 . (21)
. (21)
Формула (21) определяет один из углов между прямыми. Второй угол равен π–φ.
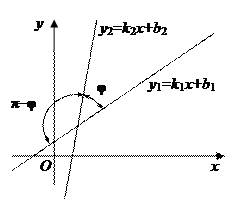

Рис.4
Если прямые параллельны, то угол между ними равен нулю и k 1 = k 2.
Если прямые перпендикулярны, то φ = 90° и
 (22)
(22)
Пример 4. Даны координаты вершин треугольника: А (6;-1), В (0;7), С (2;1). Требуется найти:
1) уравнение и длину стороны ВС;
2) уравнение и длину высоты, проведённой из вершины А;
3) уравнение медианы, проведённой из вершины А;
4) площадь треугольника.
Сделать чертёж.
Решение. 1) Сторону ВС можно рассматривать как прямую, проходящую через две заданные точки В (0;7) и С (2;1), поэтому для составления её уравнения воспользуемся формулой (19):

После преобразований получим 3 х + у –7=0. Это общее уравнение прямой ВС. Решим его относительно y и получим уравнение с угловым коэффициентом: у =-3 х +7. Из него найдём угловой коэффициент прямой ВС: kBC =-3.
|
|
|
Длину стороны ВС найдем как расстояние между двумя точками В и С (формула 8):

Высоту, проведённую из вершины А (прямая АК на рис.5) будем рассматривать как прямую, проходящую через данную точку А (6;-1) перпендикулярно прямой ВС. Тогда по условию перпендикулярности двух прямых (формула 22) найдём:

Уравнение высоты АК составим по формуле (18):
 или x -3 y -9=0.
или x -3 y -9=0.
Длину высоты АК найдём как расстояние от точки А до прямой ВС по формуле (20):

3) Медиана из вершины А делит противоположную сторону ВС пополам. Известно, что координаты середины отрезка (обозначим эту точку М) равны полусуммам одноимённых координат концов, то есть
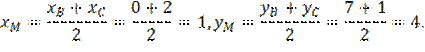
Теперь составим уравнение медианы АM, так как известны две точки А (6;-1) и М (1;4), лежащие на ней:

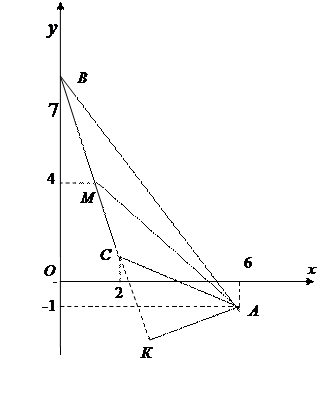
Рис. 5
После преобразований получим уравнение медианы АМ: х + у –5=0.
4) Площадь треугольника найдём по известной формуле:

В системе координат Оху строим треугольник, высоту АК и медиану АМ (рис.5).
3.3. Кривые второго порядка
Так называются линии, уравнения которых в прямоугольной системе координат являются уравнениями второй степени. К ним относятся эллипс, гипербола и парабола.
Канонические (простейшие) уравнения этих кривых и их графики приведены в таблице 1.
Пример 5. Определить и построить кривые:
а)3 х 2+4 у 2=12, б) 9 х 2-4 у 2=36, в) х 2=  .
.
Решение. а) Приведём уравнение 3 х 2+4 у 2=12 к каноническому виду. Для этого обе части уравнения разделим на свободный член, то есть на 12:
 ,
, 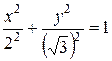 (a =2, b =3).
(a =2, b =3).
По таблице 1 устанавливаем, что это эллипс (переменные х и у входят в уравнение в квадратах, знаки при них одинаковые положительные). Из полученного уравнения определяем полуоси а =2, b =  . Строим эллипс:
. Строим эллипс:
 |
Точки А 1, А 2, В 1, В 2 называются вершинами эллипса.
б) Приведём уравнение 9 х 2–4 у 2=36 к каноническому виду, разделив обе части уравнения на 36:
 , или
, или  .
.
По табл.1 устанавливаем, что дана гапербола (переменные х и у входят в уравнение в квадратах, знаки при них разные). Положительному знаку при х 2 геометрически соответствует пересечение кривой с осью Ох.
Таблица1.
1. Эллипс  При а > b,
При а > b,  При a < b, При a < b, 
 
| ||||||||||||||||||||||||||
2. Гипербола
| ||||||||||||||||||||||||||
3. Парабола у 2 =2 рх, p >0
у 2 = -2 рх, х 2 = 2 ру, х 2 = – 2 ру
|
Построение начинаем с характеристического прямоугольника со сторонами 2 а =4 и 2 b =6; проводим его диагонали. Они служат асимптотами гиперболы. Затем строим кривую, обращая внимание на то, что при удалении в бесконечность точки гиперболы неограниченно приближаются к асимптотам. Точки А 1 и А 2 называются вершинами гиперболы и лежат на оси Ох, которая в этом случае называется действительной осью симметрии гиперболы.
 |
в) По табл.1 устанавливаем, что при наличии в уравнении х 2=  квадрата только одной переменной (x) и первой степени другой (у) задано каноническое уравнение параболы, ветви которой симметричны оси Оу и направлены вниз.
квадрата только одной переменной (x) и первой степени другой (у) задано каноническое уравнение параболы, ветви которой симметричны оси Оу и направлены вниз.
Для уточнения графика найдём на параболе дополнительные точки. Например, при у =–3 из данного уравнения параболы получим  , х 1=2, х 2=–2. Точки А 1(2, -3) и А 2(-2, -3) расположены на кривой симметрично относительно оси Оу.
, х 1=2, х 2=–2. Точки А 1(2, -3) и А 2(-2, -3) расположены на кривой симметрично относительно оси Оу.

4. Аналитическая геометрия в пространстве
4.1. Плоскость
В прямоугольной системе координат Оxyz уравнение
Ах + Ву + Сz + D =0 (23)
определяет некоторую плоскость.
Здесь х, у, z — координаты любой точки, лежащей на этой плоскости, они называются текущими координатами. Уравнение (23) называется общим уравнением плоскости. Числа А, В, С в уравнении (23) являются координатами вектора  , перпендикулярного к этой плоскости и называемого нормальным вектором плоскости.
, перпендикулярного к этой плоскости и называемого нормальным вектором плоскости.
Уравнение плоскости, проходящей через заданную точку М 0(х 0, у 0, z 0) перпендикулярно вектору 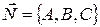 имеет вид:
имеет вид:
А (х – х 0) + В (у – у 0) + С (z – z 0) = 0. (24)
Если заданы три точки М 1(x 1, y 1, z 1), М 2(x 2, y 2, z 2), М 3(x 3, y 3, z 3),
то плоскость, проходящая через эти точки, определяется уравнением:
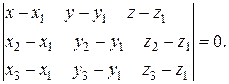 (25)
(25)
Расстояние d от точки М 0(х 0, у 0, z 0) до плоскости Ах + Ву + Сz + D =0 находится по формуле:
 (26)
(26)
4.2. Прямая в пространстве
Всякую прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, поэтому в прямоугольной системе координат прямая задаётся двумя уравнениями первой степени.
Пусть прямая проходит через данную точку М 0 (х 0, у 0, z 0) параллельно заданному вектору  , тогда её уравнения имеют вид:
, тогда её уравнения имеют вид:
 (27)
(27)
Уравнения (27) называются каноническими уравнениями прямой, а вектор 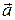 — направляющим вектором прямой.
— направляющим вектором прямой.
Если на прямой заданы две точки М 1(х 1, у 1, z 1) и М 2(х 2, у 2, z 2), то в качестве направляющего вектора этой прямой можно взять вектор  и уравнения прямой записать в виде:
и уравнения прямой записать в виде:
 (28)
(28)
Пример 5.
Даны координаты вершин пирамиды А 1 (1; 2; 3), А 2 (-2; 4; 1), А 3 (7; 6; 3), А 4 (4; -3; -1). Требуется найти:
1) уравнение плоскости А 1 А 2 А 3;
2) уравнения прямой А 1 А 2;
3) уравнения высоты, опущенной из вершины А4 на грань А1А2А3 и её длину.
Решение. 1) Уравнение плоскости А 1 А 2 А 3 составим по формуле (25), так как известны три точки, лежащие на ней:
 =0,
=0,  =0,
=0,

Вычислим последнее выражение и после преобразований получим общее уравнение плоскости А 1 А 2 А 3: 2 х –3 у –6 z +22=0.
2) Прямая А 1 А 2 проходит через заданные точки. Поэтому её уравнения составим по формуле (28):
 или
или  .
.
3) Из уравнения плоскости А 1 А 2 А 3 2 х –3 у –6 z +22=0 найдём координаты нормального вектора этой плоскости:  .
.
Для высоты пирамиды, опущенной из вершины А 4 (4; -3; -1) вектор  можно принять за направляющий, поэтому по формуле (27) получим уравнения высоты:
можно принять за направляющий, поэтому по формуле (27) получим уравнения высоты:

Длину высоты найдём как расстояние от точки А 4 до плоскости А 1 А 2 А 3 по формуле (26):

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Задание № 1. Даны координаты вершин пирамиды А 1, А 2, А 3, А 4.
Требуется найти:
1) координаты и модули векторов  и
и  ;
; 
2) угол между рёбрами А 1 А 2 и А 1 А 4;
3) площадь грани А 1 А 2 А 3;
4) объём пирамиды;
5) уравнение плоскости А 1 А 2 А 3;
6) уравнения прямой А 1 А 2;
7) уравнения высоты и её длину, опущенной из вершины А 4 на грань А 1 А 2 А 3. Сделать чертёж.
Вариант 1. А 1(-1;2;1), А 2(-2;2;5), А 3(-3;3;1), А 4(-1;4;3).
Вариант 2. А 1(-2;1;-1), А 2(-3;1;3), А 3(-4;2;-1), А 4(-2;3;1).
Вариант 3. А 1(1;1;2), А 2(0;1;6), А 3(-1;2;2), А 4(1;3;4).
Вариант 4. А 1(-1;-2;1), А 2(-2;-2;5), А 3(-3;-1;1), А 4(-1;0;3).
Вариант 5. А 1(2;-1;1), А 2(1;-1;5), А 3(0;0;1), А 4(2;1;3).
Вариант 6. А 1(-1;1;-2), А 2(-2;1;2), А 3(-3;2;-2), А 4(-1;3;0).
Вариант 7. А 1(1;2;1), А 2(0;2;5), А 3(-1;3;1), А 4(1;4;3).
Вариант 8. А 1(-2;-1;1), А 2(-3;-1;5), А 3(-4;0;1), А 4(-2;1;3).
Вариант 9. А 1(1;-1;2), А 2(0;-1;6), А 3(-1;0;2), А 4(1;1;4).
Вариант 10. А 1(1;-2;1), А 2(0;-2;5), А 3(-1;-1;1), А 4(1;0;3).
Вариант 11. А 1(0;3;2), А 2(-1;3;6), А 3(-2;4;2), А 4(0;5;4).
Вариант 12. А 1(-1;2;0), А 2(-2;2;4), А 3(-3;3;0), А 4(-1;4;2).
Вариант 13. А 1(2;2;3), А 2(1;2;7), А 3(0;3;3), А 4(2;4;5).
Вариант 14. А 1(0;-1;2), А 2(-1;-1;6), А 3(-2;0;2), А 4(0;1;4).
Вариант 15. А 1(3;0;2), А 2(2;0;6), А 3(1;1;2), А 4(3;2;4).
Вариант 16. А 1(0;2;-1), А 2(-1;2;3), А 3(-2;3;7), А 4(0;4;1).
Вариант 17. А 1(2;3;2), А 2(1;3;6), А 3(0;4;2), А 4(2;5;4).
Вариант 18. А 1(-1;0;2), А 2(-2;0;6), А 3(-3;1;2), А 4(-1;2;4).
Вариант 19. А 1(2;0;3), А 2(1;0;7), А 3(0;1;3), А 4(2;2;5).
Вариант 20. А 1(2;-1;2), А 2(1;-1;6), А 3(0;0;2), А 4(2;1;4).
Вариант 21. А 1(2;1;-4), А 2(1;-2;3), А 3(1;-2;-3), А 4(5;-2;1).
Вариант 22. А 1(2;-1;3), А 2(-5;1;1), А 3(0;3;-4), А 4(-1;-3;4).
Вариант 23. А 1(5;3;2), А 2(1;-8;8), А 3(4;-1;2), А 4(1;4;-1).
Вариант 24. А 1(-2;3;4), А 2(4;2;-1), А 3(2;-1;4), А 4(-1;-1;1).
Вариант 25. А 1(4;-4;0), А 2(-5;3;2), А 3(8;0;1), А 4(2;2;3).
Вариант 26. А 1(-3;-4;0), А 2(0;-1;3), А 3(-6;4;2), А 4(-3;0;3).
Вариант 27. А 1(0;4;-4), А 2(5;1;-1), А 3(-1;-1;3), А 4(0;-3;7).
Вариант 28. А 1(0;-6;3), А 2(3;3;-3), А 3(-3;-5;2), А 4(-1;-4;0).
Вариант 29. А 1(2;-1;-3), А 2(0;0;0), А 3(5;-1;-1), А 4(-1;-1;1).
Вариант 30. А 1(1;5;8), А 2(-2;1;4), А 3(3;-2;-3), А 4(1;-1;0).
Задание № 2. Решить систему уравнений с помощью формул Крамера.
Вариант 1. 
Вариант 2. 
Вариант 3. 
Вариант 4. 
Вариант 5. 
Вариант 6. 
Вариант 7. 
Вариант 8. 
Вариант 9. 
Вариант 10. 
Вариант 11. 
Вариант 12. 
Вариант 13. 
Вариант 14. 
Вариант 15. 
Вариант 16. 
Вариант 17. 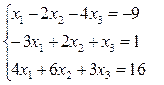
Вариант 18. 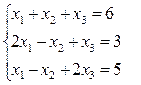
Вариант 19. 
Вариант 20. 
Вариант 21. 
Вариант 22. 
Вариант 23. 
Вариант 24. 
Вариант 25. 
Вариант 26. 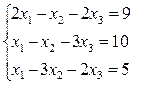
Вариант 27. 
Вариант 28. 
Вариант 29. 
Вариант 30. 
Задание №3. Даны координаты вершин треугольника А, В, С.
Требуется найти:
1) уравнение и длину стороны ВС;
2) уравнение и длину высоты, проведённой из вершины А;
3) уравнение медианы, проведённой из вершины А;
4) площадь треугольника.
Сделать чертёж.
Вариант 1. А (3;1), B (-13;-11), C (-6;13).
Вариант 2. А (26;-5), B (2;2), C (-2;-1).
Вариант 3. А (-2;3), B (-18;-9), C (-11;15).
Вариант 4. А (28;2), B (4;-5), C (0;-2).
Вариант 5. А (8;-1), B (-8;11), C (-1;-13).
Вариант 6. А (17;-4), B (-7;-11), C (-11;-8).
Вариант 7. А (9;-3), B (-7;-15), C (0;9).
Вариант 8. А (18;3), B (-6;10), C (-10;7).
Вариант 9. А (7;4), B (-9;-8), C (-2;16).
Вариант 10. А (19;3), B (-5;-4), C (-9;-1).
Вариант 11. А (5;1), B (1;-2), C (-4;10).
Вариант 12. А (14;10), B (-2;-2), C (5;22).
Вариант 13. А (-13;3), B (-1;-2), C (2;2).
Вариант 14. А (22;-6), B (-2;1), C (-6;-2).
Вариант 15. А (22;4), B (-2;-3), C (-6;0).
Вариант 16. А (6;0), B (2;-3), C (-3;9).
Вариант 17. А (15;9), B (-1;-3), C (6;21).
Вариант 18. А (-8;3), B (4;-2), C (7;2).
Вариант 19. А (20;-2), B (-4;5), C (-8;2).
Вариант 20. А (23;5), B (-1;-2), C (-5;1).
Вариант 21. А (4;7), B (0;-2), C (-1;6).
Вариант 22. А (7;13), B (1;5), C (-5;4).
Вариант 23. А (-6;-3), B (1;2), C (-2;0).
Вариант 24. А (-9;11), B (4;7), C (-2;-1).
Вариант 25. А (2;-8), B (-3;4), C (-3;-1).
Вариант 26. А (1;-12), B (2;-2), C (-8;1).
Вариант 27. А (4;-3), B (-2;-1), C (3;-2).
Вариант 28. А (7;0), B (-1;3), C (3;0).
Вариант 29. А (-5;6), B (-4;0), C (-2;3).
Вариант 30. А (2;6), B (-6;2), C (-6;4).
Задание №4. Определить и построить кривые.
Вариант 1. а) 16х2 + 3у2 = 48; б) х2 - у2 = 4; в) х2 = - 4у.
Вариант 2. а) 9х2 + 25у2 = 225; б) х2 - 18у2 = 36; в) у2 = - х.
Вариант 3. а) 25х2 + 6у2 = 150; б) -х2 + у2 = 9; в) у2 = 3х.
Вариант 4. а) 4х2 + 5у2 = 20; б) х2 - 25у2 = 25; в) х2 = -8у.
Вариант 5. а) 9х2 + у2 = 9; б) х2 - у2 = 16; в) х2 = 9.
Вариант 6. а) 3х2 + у2 = 3; б) -10х2 + у2 = 10; в) у2 = 5х.
Вариант 7. а) 16х2 + 5у2 = 80; б) - 4х2 + 9у2 = 36; в) у2 = -8х.
Вариант 8. а) 9х2 + 3у2 = 27; б) -х2 + у2 = 16; в) х2 = 14у.
Вариант 9. а) 25х2 + 7у2 = 175; б) 4х2 - 16у2 = 64; в) х2 = -15у.
Вариант 10. а) х2 + у2 = 5; б) - 4х2 + у2 = 4; в) у2 = 8х.
Вариант 11. а) 9х2 + 21у2 = 189; б) х2 - 3у2 = 3; в) у2 = -2х.
Вариант 12. а) х2 + 5у2 = 5; б) -4х2 + у2 = 4; в) 2х2 = 3у.
Вариант 13. а) 3х2 + 8у2 = 24; б) х2 - у2 = 1; в) 7х2 = -2у.
Вариант 14. а) х2 + 9у2 = 1; б) 16х2 - 9у2 = 144; в) у2 = 7х.
Вариант 15. а) 25х2 + у2 = 1; б) -х2 + у2 = 4; в) у2 = -9х.
Вариант 16. а) 16х2 + 2у2 = 32; б) 9х2 - 5у2 = 45; в) х2 = -7у.
Вариант 17. а) 9х2 + 4у2 = 36; б) 5х2 - 4у2 = 20; в) х2 = у.
Вариант 18. а) 16х2 + 9у2 = 144; б) - 5х2 + у2 = 5; в) у2 = 5х.
Вариант 19. а) 9х2 + 5у2 = 45; б) х2 - у2 = 16; в) у2 = -4х.
Вариант 20. а) 4х2 + у2 = 4; б) - 15х2 + 4у2 = 60; в) х2 = 6у.
Вариант 21. а) х2 + 3у2 = 3; б) - 9х2 + 7у2 = 63; в) х2 = -у.
Вариант 22. а) 16х2 + у2 = 160; б) 3х2 - 16у2 = 48; в) у2 = 4х.
Вариант 23. а) 5х2 + 9у2 = 45; б) 7х2 - 16у2 = 112; в) у2 = -7х.
Вариант 24. а) 4х2 + 12у2 = 1; б) 16х2 - у2 = 64; в) 2х2 = 5у.
Вариант 25. а) 81х2 + 25у2 = 1; б) -х2 + 9у2 = 81; в) 3х2 = -4у.
Вариант 26. а) 7х2 + у2 = 7; б) 4х2 - 13у2 = 52; в) 3у2 = -х.
Вариант 27. а) х2 + 10у2 = 10; б) 9х2 - 25у2 = 225; в) 2у2 = х.
Вариант 28. а) 10х2 + 16у2 = 1; б) -8х2 + 9у2 = 72; в) х2 = -2у.
Вариант 29. а) 25х2 + у2 = 25; б) 4х2 - 9у2 = 1; в) х2 = 3у.
Вариант 30. а) х2 + 8у2 = 16; б) -121х2 + у2 = 121; в) у2 = -2х.
Библиографический список
1. Шипачев В.С. Высшая математика. М.: Высш. шк., 2005. — 479 с.
2. Кадомцев С.Б. Аналитическая геометрия и линейная алгебра. — М.: физ.-мат. лит., 2001.
3. Данко П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для вузов:
в 2 ч. / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. — М.: Изд. дом «ОНИКС 21 век»: Мир и Образование, 2003. — 304 с.
 2015-10-22
2015-10-22 546
546