Моменты случайных величин

Моменты служат для описания основных свойств плотно­сти вероятности случайной величины. Они содержат меньше инфор­мации о случайной величине по сравнению с плотностью вероятно­сти, но часто более удобны при решении технических задач. В каче­стве моментов скалярной случайной величины чаще всего применяются математическое ожидание и дисперсия (или среднеквадратическое отклонение).

Математическим ожиданием некоторой функции y = f(x) случай­ной величины х называется интеграл

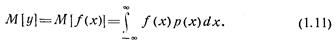
При f(x) = x^R величина M[x^R]=m_x^R называется начальным моментом R-го порядка случайной величины х. Начальный омент пер­вого порядка т_х называется математическим ожиданием случайной величины х:

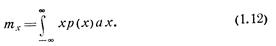
По реализациям математическое ожидание т_х может быть оценено как статистическое среднее

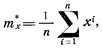
причем .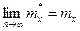

Разность менаду случайной величиной х и ее мате­матическим ожиданием т_х называется центрированной случайной величиной. Центральный момент R-го порядка скалярной случайной величины х определяется как математическое ожидание R-й степени соответствующей центрированной случайной величины:

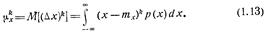
Центральный момент второго порядка называется дис­персией случайной величины х:

По реализациям оценку 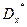можно рассчитать по формуле

причем .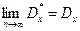

Дисперсия характеризует рассеивание значений случайной вели­чины х в окрестности ее математического ожидания т_х. Наряду с дисперсией D_x в качестве меры рассеивания рассматривают и среднеквадратическое отклонение .

Центральные моменты высших порядков определяют аналогич­но. Например, центральный момент третьего порядка

Он характеризует асимметрию кривой плотности вероятности р(х). Если р(x) —симметричная функция с осью симметрии, проходящей через т_х, то , а также все другие нечетные центральные момен­ты случайной величины х равны нулю.

В качестве характеристик вероятностной зависимости двух ска­лярных случайных величин х и у рассматривают их корреляцион­ный момент

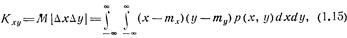
или коэффициент корреляции

вычисляемый при и .

По реализациям хⁱ, уⁱ, i= 1, п, случайных величин x и y их корре­ляционный момент можно оценить с помощью соотношения

Если случайные величины х и у связаны между собой линейной зависимостью у = ах + b, где а и b — произвольные неслучайные числа, то , а r_xy=1 при а>1 и r_xy = -1 при а<0.

Случайные величины х и у называют некоррелированными, если . Используя формулы (1.15), (1.10), нетрудно пока­зать, что из независимости случайных величин следует их некорре­лированность. Обратное утверждение в общем случае неверно. Ина­че говоря, условие независимости случайных величин более сильное, чем условие некоррелированности.

Для векторной случайной величины х простейшими моментными характеристиками, наиболее часто рассматриваемыми при прак­тических расчетах, являются вектор математических ожиданий т_х и корреляционная матрица К_х- Составляющими вектора т_х являются математические ожидания компонент вектора х, т. е. .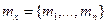

Корреляционной матрицей К_х случайного вектора х называется симметричная матрица, составленная из корреляционных моментов , и дисперсий 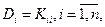составляющих век­тора х:

причем .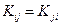

Если все составляющие случайного вектора х взаимно некорре­лированные, то этот вектор называют некоррелированным. Корре­ляционная матрица К_х некоррелированного вектора — диагональ­ная, все ее внедиагональные элементы равны нулю.