Численное интегрирование

Постановка задачи

 

Пусть требуется вычислить определенный интеграл

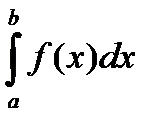, (1)

где f (x)– непрерывная на отрезке [ a; b ] функция.

О

y = f(x)

b

a

y

x

С геометрической точки зрения интеграл (1) при f(x) > 0 равен площади криволинейной трапеции, ограниченной кривой y = f(x), осью Ox и прямыми x = a, x = b (рис. 14). Другими словами, 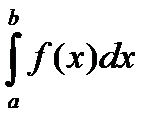равен площади заштрихованной фигуры на рис. 14.

Рисунок 14 – Геометрический смысл определенного интеграла.

 

Вычислить определенный интеграл (1) можно с помощью аналитической формулы Ньютона-Лейбница 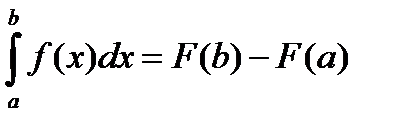(2):

, (2)

где F (x) – первообразная функция для заданной функции f (x).

Однако во многих случаях не удается найти никакой аналитической формулы в виду невозможности определения F(x).

Таким интегралом, например, является 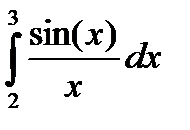. (3)

В математическом анализе доказывается, что для данной подынтегральной функции нельзя выразить первообразную F(x) через элементарные функции. С другой стороны площадь криволинейной трапеции, задаваемой интегралом (3) существует (рис. 16). Значит, должно существовать и значение интеграла, которое, однако, мы не можем найти точно.

Рисунок –15. График функции 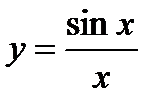на отрезке [1; 3].

В таких случаях приходится применять методы численного интегрирования.

Основной принцип построения всех приближенных формул численного интегрирования состоит в том, что интервал интегрирования разбивается на множество меньших отрезков, внутри которых подынтегральная кривая y = f(x) заменяется с некоторой степенью точности более простыми функциями, интегралы от которых можно вычислить. С геометрической точки зрения выполняется следующее: искомая площадь криволинейной трапеции приближенно заменяется суммой площадей элементарных геометрических фигур.