Ой учебный вопрос. Решение задач в условиях определенности

 

Задача 1. Об использовании ресурсов или задача планирования производства.

Для изготовления двух видов продукции Р₁ и Р₂ используют четыре вида ресурсов S₁, S₂, S₃, S₄.

Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице:

 

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление продукции
Р1	Р2
S1
S2
S3		-
S4			-

 

Прибыль, получаемая от единицы продукции Р₁ и Р₂, соответственно 2 и 3 руб.

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

 

Решение.

Составим экономико-математическую модель задачи.

Обозначим за х₁, х₂ – число единиц продукции соответственно Р1 и Р₂, запланированных к производству.

Для их изготовления потребуется:

· х₁+3х₂ единиц ресурса S₁;

· 2х₁ + х₂ единиц ресурса S₂;

· х₂ единиц ресурса S₃;

· 3х₁ единиц ресурса S₄.

 

Так как потребление ресурсов S₁, S₂, S₃, S₄. не должно превышать запасов, соответственно 18, 16, 45 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:

 

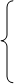х₁+3х₂ <= 18

2х₁ + х₂<= 16

х₂ <= 45

3х₁ <= 21

 

По смыслу задачи переменныех₁>=0, x₂>=0.

 

Суммарная прибыль F составит 2х₁ руб. от реализации продукции Р₁ и 3х₂ руб. – от реализации продукции Р₂, т.е.

 

F = 2х₁+3х₂

 

Итак, экономико-математическая модель задачи построена.

 

Графическое решение: общая постановка задачи линейного программирования.

 

Дана система m линейных уравнений и неравенств с n переменными – называемыми балансовыми условиями:

 

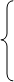А₁₁х₁+а₁₂х₂+…+а_1nх_n<=b₁

………………………....b₂

…………………………b_k

………………………....b_m

 

И линейная функция (называемая целевой функцией):

 

F=c₁x₁ + c₂x₂ + …+c_nx_n

 

Необходимо найти такое решение Х=(х₁,х₂,…,х_j,…,х_n),

Где х_j>=0 (j-1,2,…,l; l<=n) – Граничные условия

При котором линейная функция принимает оптимальное (т.е. максимальное или минимальное) значение.

Система линейных уравнений называется системой ограничений, а функция F – целевой функцией.

Более коротко задачу Линейного программирования можно представить в виде:

 

F= сумма от 1 до n С_jx_j max (или min)

 

При ограничениях:

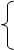сумма от 1 по nа_ijx_ij<=bi (i = 1,2,…,k)

сумма от 1 по nа_ijx_ij = bi (i = k+1, k+2,…,m)

 

x>=0 (j=1,2,…,l;l<=n).

Оптимальным решением задачи линейного программирования называется решение X=(x₁,x₂,…,x_j,…,x_n) балансовой системы ограничений, удовлетворяющее граничным условиям, при котором целевая функция принимает оптимальное (максимальное или минимальное) значение.

Теорема: Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек.

 

Решим геометрически задачу рассмотренную выше:

 

F=2x₁+3х₂ max

 

При ограничениях:

 

х₁+3х₂ <= 18 x₁>=0, х₂>=0

2х₁ + х₂<= 16

х₂ <= 45

3х₁ <= 21

 

Решение: Для построения искомого множества решений системы неравенств строим последовательно множество решений каждого неравенства.

Построим границу полуплоскости - прямую x₁+3х₂ = 18, найдя точки ее пересечения с осями координат. Для определения искомой полуплоскости (верхней или нижней) рекомендуется задать произвольную контрольную точку, не лежащую на ее границе (построенной прямой). Если неравенство выполняется в контрольной точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и выполняется во всех точках другой полуплоскости.

В качестве контрольной точки удобно взять начало координат О(0,0), не лежащее на построенной прямой. Координаты точки О(0,0) удовлетворяют неравенству x₁+3х₂<= 18,следовательно решением этого неравенства является нижняя полуплоскость, содержащая контрольную точку О(0,0)

И так повторяем со всеми неравенствами.

 

Рассмотрим так называемую линию уровня линейной функции F, т.е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение а, т.е.

 

F=а, или с₁x₁+c₂х₂=a

 

Построим линии уровня для линейной функции в рассмотренной нами задачи.

 

Очевидно, что линия уровня при F=0 проходит через начало координат. Зададим, например F=6 и построим линию уровня 2x₁+3х₂=6. Ее направление указывает на направление возрастания линейной функции (вектор q). Так как рассматриваемая задача на отыскание максимума, то оптимальное решение – в угловой точке С, находящейся на пересечении прямых I и II, т.е. координаты точки С определяются решением системы уравнений:

 

x₁+3х₂ = 18

2x₁+х₂=16

 

Откуда x₁=6, х₂ = 4, т.е. С(6;4).

Максимум линейной функции равен F_max = 2*6+3*4=24.

 

Итак F_max =24 при оптимальном решении x₁=6, х₂=4, т.е. максимальная прибыль в 24 руб. может быть достигнута при производстве 6 единиц продукции Р1 и 4 единиц продукции Р2.