2018-01-08
1250Линейное программирование – один из первых и наиболее подробно изученных разделов математического программирования в смысле нахождения оптимальных значений переменных. Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного описания реальных экономических процессов.
Линейное программирование применяется при решении экономических задач оптимального управления и планирования производства; определение оптимального размещения оборудования; определение оптимального плана перевозок груза (транспортная задача); оптимальное распределение кадров и т.д.
Задача линейного программирования (ЗЛП), состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.
Наряду с общей формой широко используются также каноническая и стандартная формы. Как в канонической, так и в стандартной форме все переменные в любом допустимом решении задачи должны принимать неотрицательные значения (такие переменные принято называть неотрицательными в отличие от так называемых свободных переменных, на область значений которых подобное ограничение не накладывается). Задача линейного программирования в канонической форме при поиске минимума целевой функции может иметь вид:
|
|
|
w = cx ® min
Ax = b, x ≥ 0.
Задача линейного программирования в стандартной форме:
w = cx ® min,
Ax ≥ b, x ≥ 0.
В обоих случаях A есть матрица размерности m×n. Большинство экономических задач, решаемых методами ЗЛП, может быть сформулировано так: максимизировать некоторую экономическую целевую функцию F (x1,x2,…xn) при нескольких ограничениях: g1 (x1,…xn)≤ b1;
g2 (x1,…xn)≤ b2;
……………….
gm (x1,…xn)≤ bm,
здесь F (x1,x2,…xn) – целевая функция, ее экстремум - критерий эффективности (например, прибыль от производства продукции, стоимость перевозок и т.п); X = { x1,…xn } – варьируемые параметры; g1 (X),…, gm(X) – функции, которые задают ограничения на имеющиеся ресурсы.
В рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, транспортные задачи и прочие.
Некоторые из них. Определение оптимального ассортимента.
Имеются m видов ресурсов в количествах b1,b2,…,bi,…, bm и n видов изделий. Задана матрица A = || aij ||, i = 1,…, n, где aij характеризует нормы расхода i -го ресурса на единицу j -го вида изделий. Эффективность производства j -го вида изделий характеризуется Cj, удовлетворяющим условию линейности. Нужно определить такой план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности будет наибольший.
|
|
|
Обозначим количество единиц k -го вида изделий, выпускаемых предприятием, через xk, k = 1, K. Тогда математическая модель этой задачи будет иметь такой вид:
максимизировать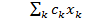 
при ограничениях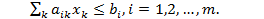 
Кроме ограничений на ресурсы (1), в эту модель можно ввести дополнительные ограничения на планируемый уровень выпуска продукции x j ≥ x j0, xi: xj: xk = bi: bj: bk для всех i, j, k и т.д.
Оптимальное распределение взаимозаменяемых ресурсов.
Имеются m видов взаимозаменяемых ресурсов a1,a2,…am, используемых при выполнении n различных работ (задач). Объемы работ, которые должны быть выполнены, составляют b1,b2,…,bi,…, bn единиц. Заданы числа λ ij, указывающие, сколько единиц j- й работы можно получить из единицы i -го ресурса, а также Cij – затраты на производство j -й работы из единицы i -го ресурса. Требуется распределить ресурсы по работам таким образом, чтобы суммарная эффективность выполненных работ была максимальной (или суммарные затраты – минимальными).
Данная задача называется общей распределительной задачей. Количество единиц i -го ресурса, которое выделено на выполнение работ j- го вида, обозначим xij.
Математическая модель рассматриваемой задачи такова:
Минимизировать функцию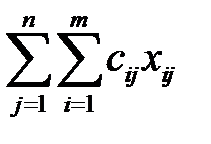 
при ограничениях 
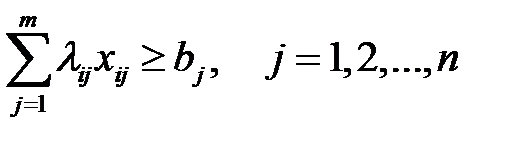(2).
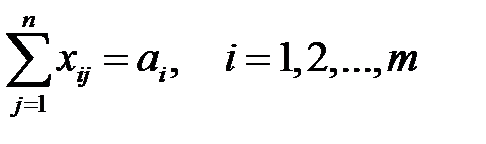(3) Ограничение (2) означает, что план всех работ должен быть выполнен полностью, а (3) – что ресурсы должны быть израсходованы целиком. Примером этой задачи может быть задача о распределении самолетов по авиалиниям. Наряду с линейным применяются методы нелинейного, дискретного и динамического программирования. Задача оптимизации функции полезности 
, 
, 
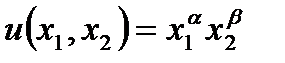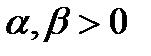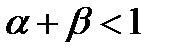при ограничениях на бюджет 
, 
, 
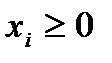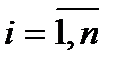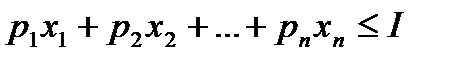- нелинейная. Здесь 
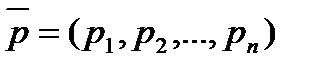— вектор цен на набор из n продуктов 
, 
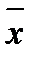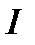— доход индивида, который он готов потратить на приобретение набора продуктов 
.
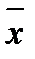В методах динамического программирования используется аддитивная целевая функция в виде суммы результирующих показателей по этапам - одни решения приводят к необходимости принимать последующие решения, то есть происходит цепь последовательных решений. В качестве примера можно рассмотреть задачу о назначениях:
Директор хочет выбрать на работу помощника-секретаря и имеет возможность испытать 3х кандидатов. Известно, что на прием могут прийти секретари трех уровней квалификации, которым можно присвоить баллы: 1) отличный – 3 балла, 2) хороший – 2 балла, 3) посредственный – 1 балл. Известна статистика рынка секретарей каждой квалификации, определяемая вероятностями: Отл. Р= 0,2; Хор. Р= 0,3; Поср. Р= 0,5.
Если кандидату отказано, то он покидает дирекцию, не ожидая.
По методам динамического программирования начинают анализ с конца.
А). Рассмотрим последний этап. Какую ситуацию получим на III этапе? Т.к. третий секретарь будет обязательно принят, то с учетом вероятностей значение аддитивной целевой оценочной функции в баллах, которую мы получим как математическое ожидание (среднее), будет.
а 3 = 3*0,2 + 2*0,3 + 1*0,5 = 1,7
Б). Вернемся на предыдущий этап II-го шага
На втором этапе, если получим отличного (3 балла) секретаря с вероятностью 0,2 – принимаем на работу; если посредственного (1 балл) с вероятностью этого 0,5, то обязательно продолжим на третьем этапе, если же получим хорошего (2 балла) – вероятность 0,3 и остановимся, то в среднем на 2-м этапе получим:
а 2 = 3*0,2 + 2*0,3 + 1,7*0,5 = 2,05
В). Предыдущий этап – первый. Средний выигрыш, который будет, если на 1-м этапе отл.- принимать, хор.-продолжать, поср.- продолжать будет такой:
а 1 = 3*0,2 + 2,05*0,3 + 2,05*0,5 = 2,24
Т.е. за счет того, что мы испытываем трех кандидатов мы получим дополнительный выигрыш качества: ∆ = 2,24 – 1,7 = 0,54
