Выпуклость и вогнутость функции. Точки перегиба

 

Направление выпуклости кривой является важной характеристикой ее формы.

Понятие о выпуклости, вогнутости и точках перегиба функции 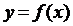дадим, исходя из рис. 6. На этом рисунке изображен график функции, выпуклой на интервале , вогнутой на интервале , и y которой точка x ₀, разделяющая интервалы выпуклости и вогнутости, есть точка перегиба функции . Кстати, точка M ₀ называется точкой перегиба графика функции (не путать точку перегиба функции x ₀ и точку перегиба её графика M ₀). Интервалы выпуклости, вогнутости и точки перегиба функции – важные характеристики любой функции, поэтому полезно уметь их находить.

Рассмотрим подробнее функцию 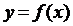на ее интервале выпуклости (рис. 7 (а)) и на ее интервале вогнутости (рис. 7 (б)).

Для выпуклой функции (рис. 7 (а)) касательная к ее графику в любой его точке расположена выше графика, причем с увеличением абсциссы x точки касания эта касательная поворачивается по часовой стрелке. Это значит, что с увеличением x угол 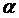наклона касательной к оси ох уменьшается. Но тогда уменьшается и угловой коэффициент касательной . А значит, с увеличением x уменьшается (убывает) равная ему производная функции 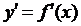. Но если некая функция убывает, то, как мы знаем, ее производная отрицательна. Значит, на всем интервале выпуклости функции .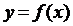

Аналогичное рассуждение приводит к выводу, что если функция 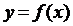вогнута на некотором интервале (см. рис. 7 (б)), то для любого x из этого интервала (проведите это рассуждение самостоятельно).

Верно, естественно, и обратное: если на некотором интервале оси ох вторая производная функции положительна, то функция вогнута на этом интервале. А если эта производная отрицательна – то функция выпукла на указанном интервале.

Определение 3. Кривая обращена выпуклостью вверх на интервале 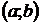, если все точки кривой лежат ниже любой ее касательной на этом интервале.

Определение 4. Кривая обращена выпуклостью вниз на интервале 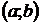, если все точки кривой лежат выше любой ее касательной на этом интервале.

Кривая, обращенная выпуклостью вверх, будет называть выпуклой, а обращенную выпуклостью вниз – вогнутой.

Теорема 5: Если во всех точках интервала 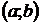вторая производная f(x) отрицательна, т.е. , то кривая y=f(x) на этом интервале обращена выпуклостью вверх (кривая выпукла)

Доказательство. Возьмем в интервале 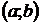произвольную точку х=х₀ и проведем касательную к кривой в точке с абсциссой х=х₀. Теорема будет доказана, если мы установим, что все точки кривой на интервале 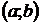лежат ниже этой касательной, т.е. что ордината любой точки кривой y=f(x) меньше ординаты y касательной при одном и том же значении х.

Уравнение кривой имеет вид

y=f(x).

Уравнение касательной к кривой в точке х=х₀ имеет вид

Откуда следует, что разность ординат кривой и касательной при одном и том же значении х равна

Применяя теорему Лагранжа к разности , получим:

,

(где с лежит между х₀ и х). К выражению, стоящему в квадратных скобках, снова применим теорему Лагранжа, тогда

.

(где с₁ лежит между х₀ и с).

Рассмотрим два случая:

1) Пусть х>x₀. Тогда x₀<c₁<c<x, поскольку . Учитывая этот факт и условие , получим .

2) Пусть х<x₀. Тогда x<c<c₁<x₀, поскольку . Учитывая этот факт и условие , получим .

Таким образом, мы доказали, что любая точка кривой лежит ниже касательной к кривой, каковы бы ни были значения х и х₀ на интервале 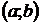. Что и означает, что кривая выпукла. Теорема доказана.

Аналогично доказывается теорема для случая вогнутой функции.

Теорема 6: Если во всех точках интервала 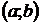вторая производная f(x) положительна, т.е. , то кривая y=f(x) на этом интервале обращена выпуклостью вниз (кривая вогнута)

 

Теперь перейдем к точкам перегиба функции. Так как эти точки разграничивают интервалы выпуклости и вогнутости и, следовательно, не принадлежат ни тем, ни другим, то в точках перегиба вторая производная функции не может быть ни положительной, ни отрицательной. А значит, в этих точках она или равна нулю, или не существует.

Но не все точки x, в которых или не существует, непременно должны быть точками перегиба. Точками перегиба будут лишь те из них, в которых вторая производная меняет знак (с (+) на (–) или с (–) на (+)). Таким образом, точки оси ох, в которых или не существует, являются лишь подозрительными на перегиб. Окончательное выяснение сути этих точек производится после исследования знака второй производной слева и справа от каждой из них. Справедлива следующая

Теорема 7. Пусть кривая определяется уравнением y=f(x). Если или не существует и при переходе через значение x=a производная меняет знак, то точка кривой с абсциссой x=a есть точка перегиба.

Из всего сказанного вытекает

схема исследования функции 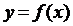на выпуклость-вогнутость
и точки перегиба:

1. Находим область определения функции, а заодно устанавливаем интервалы ее непрерывности и точки разрыва (стандартное начало любого исследования функции).

2. Находим вторую производную .

3. Находим точки (значения x), подозрительные на перегиб. То есть находим те точки (значения x), в которых вторая производная функции или равна нулю, или не существует:

а)

б) не существует

4. Наносим все найденные подозрительные на перегиб точки на область определения функции (на ось ох) и отмечаем (например, дугами) интервалы, на которые разобьется этими дугами область определения функции. В каждом из этих интервалов выясняем знак второй производной . По установленным знакам этой производной отмечаем интервалы выпуклости и вогнутости функции ((–) – выпуклость, (+) – вогнутость), а также точки перегиба функции.

5. Вычисляем значения функции 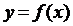во всех найденных точках ее перегиба и находим тем самым точки перегиба графика функции.

Пример 4. Исследовать на выпуклость-вогнутость и точки перегиба функцию (в примере 2 она уже исследовалась на возрастание-убывание и точки экстремума).

Решение. Реализуем изложенную выше схему.

1. Функция определена, а следовательно и непрерывна для любых x от до .

2. Найдем :

.

3. Найдем точки (значения x), подозрительные на перегиб:

а) .

б) не существует Þ таких x нет.

4. Нанесем на ось ох найденную подозрительную на перегиб точку . Ось ох (область определения функции) разобьется этой точкой на два интервала:

Определяем знаки второй производной в этих интервалах (они отмечены на рис. выше). Тем самым устанавливаем интервалы выпуклости (знак ) и вогнутости (знак ), а также устанавливаем, что – точка перегиба функции.

5. Вычисляем значение функции в точке ее перегиба и тем самым определим точку перегиба графика функции (она указана на рис. 4).