6.2.1. Постановка и классификация задач теории оптимального управления. В подавляющем большинстве рассмотренных нами задач факторы, связанные с изменением изучаемых объектов и систем в течение времени, выносились за скобки. Возможно, при выполнении определенных предпосылок такой подход является конструктивным и правомерным. Однако очевидно и то, что это допустимо далеко не всегда. Существует обширный класс задач, в которых необходимо найти оптимальные действия объекта, учитывающие динамику его состояний во времени и пространстве. Методы их решения составляют предмет математической теории оптимального управления.
В весьма общем виде задача оптимального управления может быть сформулирована следующим образом:
Имеется некоторый объект, состояние которого характеризуется двумя видами параметров — параметрами состояния и параметрами управления, причем в зависимости от выбора последних процесс управления объектом протекает тем или иным образом. Качество процесса управления оценивается с помощью некоторого функционала*, на основе чего ставится задача: найти такую последовательность значений управляющих параметров, для которой данный функционал принимает экстремальное значение.
* Функционалом называется числовая функция, аргументами которой, как правило, служат другие функции.
С формальной точки зрения многие проблемы оптимального управления могут быть сведены к задачам линейного или нелинейного программирования большой размерности, так как каждой точке пространства состояний соответствует свой вектор неизвестных переменных. Все же, как правило, движение в данном направлении без учета специфики соответствующих задач не приводит к рациональным и эффективным алгоритмам их решения. Поэтому методы решения задач оптимального управления традиционно связаны с другим математическим аппаратом, берущим свое начало от вариационного исчисления и теории интегральных уравнений. Следует также заметить, что опять-таки в силу исторических причин теория оптимального управления была ориентирована на физические и технические приложения, и ее применение для решения экономических задач носит в определенном смысле вторичный характер. В то же время в целом ряде случаев модели исследования, применяющие аппарат теории оптимального управления, могут привести к содержательным и интересным результатам.
К сказанному выше необходимо добавить замечание о тесной связи, существующей между методами, применяемыми для решения задач оптимального управления, и динамическим программированием. В одних случаях они могут использоваться на альтернативной основе, а в других довольно удачно дополнять друг друга.
Существуют различные подходы к классификации задач оптимального управления. Прежде всего, их можно классифицировать в зависимости от объекта управления:
Ø Ø задачи управления с сосредоточенными параметрами;
Ø Ø задачи управления объектами с распределенными параметрами.
Примером первых является управление самолетом как единым целым, а вторых — управление непрерывным технологическим процессом.
В зависимости от типа исходов, к которым приводят применяемые управления, выделяют детерминированные и стохастические задачи. В последнем случае результатом управления является множество исходов, описываемых вероятностями их наступления.
По характеру изменения управляемой системы во времени различают задачи:
Ø Ø с дискретно изменяющимся временем;
Ø Ø с непрерывно изменяющимся временем.
Аналогично классифицируются задачи управления объектами с дискретным или непрерывным множеством возможных состояний. Задачи управления системами, в которых время и состояния меняются дискретно, получили название задач управления конечными автоматами. Наконец, при определенных условиях могут ставиться задачи управления смешанными системами.
Многие модели управляемых систем основаны на аппарате дифференциальных уравнений как в обыкновенных, так и в частных производных. При исследовании систем с распределенными параметрами, в зависимости от вида используемых дифференциальных уравнений в частных производных, выделяют такие типы задач оптимального управления, как параболические, эллиптические или гиперболические.
Рассмотрим два простейших примера задач управления экономическими объектами.
Задача распределения ресурсов. Имеется т складов с номерами i (i ∊1: m), предназначенных для хранения однородного продукта. В дискретные моменты времени t ∊0:(T -l) происходит его распределение между объектами-потребителями (клиентами) с номерами j, j ∊1: n. Пополнение запаса в пунктах хранения продукта в t -й момент времени определяется величинами ait, i ∊1: m, а потребности клиентов в нем равняются bjt, j ∊1: n. Обозначим через cti,j — затраты на доставку единицы продукта из i -го склада j -му потребителю в момент времени t. Также предполагается, что продукт, поступивший на склад в момент t, может быть использован, начиная со следующего момента (t +l). Для сформулированной модели ставится задача найти такой план распределения ресурсов { хti,j } Tm x n , который минимизирует суммарные расходы на доставку потребителям продукции со складов в течение полного периода функционирования системы.
Обозначив через хti,j количество продукта, поставляемое j -му клиенту с i -го склада в t -й момент времени, а через zti — общее количество продукта на i -м складе, описанную выше проблему можно представить как задачу нахождения таких совокупностей переменных
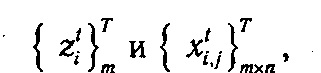
которые обращают в минимум функцию
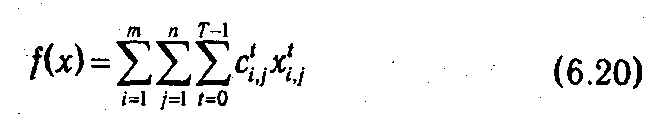
при условиях

где объемы начальных запасов продукта на складах z 0 i = ži. предполагаются заданными.
Задачу (6.20)-(6.23) называют динамической транспортной задачей линейного программирования. С точки зрения приведенный выше терминологии независимые переменные хti,j представляют собой параметры управления системой, а зависящие от них переменные zti — совокупность параметров состояния системы в каждый момент времени t. Ограничения zti ≥ 0 гарантируют, что в любой момент времени с любого склада не может быть вывезен объем продукта, превышающий его фактическое количество, а ограничения (6.21) задают правила изменения этого количества при переходе от одного периода к другому. Ограничения данного вида, которые задают условия на значения параметров состояния системы, принято называть фазовыми.
Отметим также, что условие (6.21) служит простейшим примером фазовых ограничений, поскольку связываются значения параметров состояния для двух смежных периодов t и t +l. В общем случае может устанавливаться зависимость для группы параметров, принадлежащих нескольким, возможно несмежным, этапам. Такая потребность может возникнуть, например, при учете в моделях фактора запаздывания поставок.
Простейшая динамическая модель макроэкономики. Представим экономику некоторого региона как совокупность п отраслей (j ∊1: п), валовой продукт которых в денежном выражении на некоторый момент t может быть представлен в виде вектора zt =(zt 1 , zt 2 ,..., ztn), где t ∊0:(Т -1). Обозначим через At матрицу прямых затрат, элементы которой ati,j, отражают затраты продукции i -й отрасли (в денежном выражении) на изготовление единицы продукции j -й отрасли в t -й момент времени. Если Xt = ║ xti,j ║ n x m — матрица, задающая удельные нормы продукции i -й отрасли, идущей на расширение производства в j -й отрасли, а уt = (уt 1, уt 2 ,..., уtn) — вектор объемов продукции отраслей потребления, идущей на потребление, то условие расширенного воспроизводства можно записать как
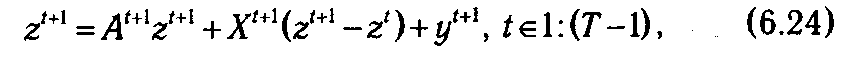
где z 0 = ž — исходный запас продукции отраслей предполагается заданным и
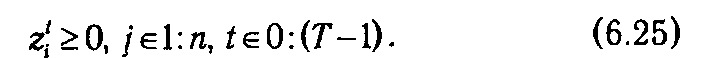
В рассматриваемой модели величины zt являются параметрами состояния системы, а Xt — управляющими параметрами. На ее базе могут быть поставлены различные задачи, типичным представителем которых является задача оптимального вывода экономики на момент Т к некоторому заданному состоянию z *. Данная задача сводится к отысканию последовательности управляющих параметров

удовлетворяющих условиям (6.24)-(6.25) и минимизирующих функцию

6.2.2. Простейшая задача оптимального управления. Один из приемов, применяемых для решения экстремальных задач, состоит в выделении некоторой проблемы, допускающей относительно несложное решение, к которой в дальнейшем могут быть сведены остальные задачи.
Рассмотрим так называемую простейшую задачу управления. Она имеет вид
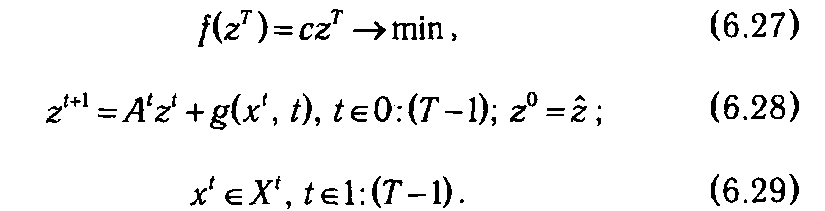
Специфика условий задачи (6.27)-(6.29) состоит в том, что функции качества управления (6.27) и ограничения (6.28) являются линейными относительно zt, в то же время функция g (t, хt), входящая в (6.28), может быть произвольной. Последнее свойство делает задачу нелинейной даже при t =1, т. е. в статическом варианте.
Общая идея решения задачи (6.27)-(6.29) сводится к ее «расщеплению» на подзадачи для каждого отдельно взятого момента времени, в предположении, что они успешно разрешимы. Построим для задачи (6.27)-(6.29) функцию Лагранжа
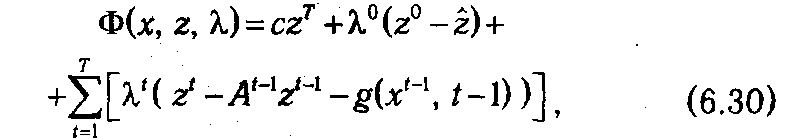
где λ t — вектора множителей Лагранжа (t ∊0: Т). Ограничения (6.29), носящие общий характер, в функцию (6.30) в данном случае не включены. Запишем ее в несколько иной форме
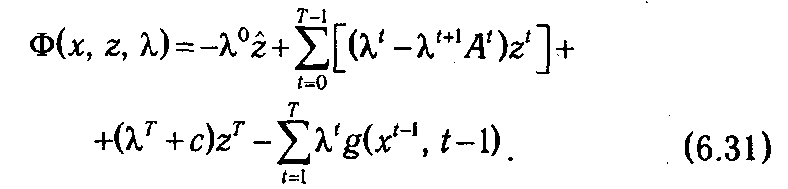
Необходимые условия экстремума функции Ф (х, z, λ) по совокупности векторов zt задаются системой уравнений
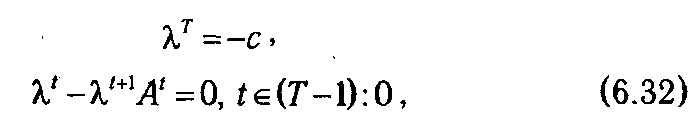
которая называется системой для сопряженных переменных. Как можно заметить, процесс нахождения параметров λ t в системе (6.32) осуществляется рекуррентным образом в обратном порядке.
Необходимые условия экстремума функции Лагранжа по переменным λ t будут эквивалентны ограничениям (6.28), и, наконец, условия ее экстремума по совокупности векторов хt ∊ Хt, t ∊1:(Т -1) должны быть найдены как результат решения задачи
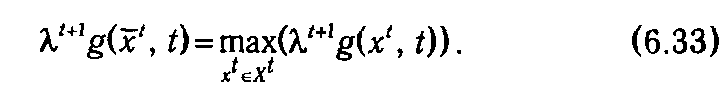
Таким образом, задача поиска оптимального управления сводится к поиску управлений, подозрительных на оптимальность, т. е. таких, для которых выполняется необходимое условие оптимальности. Это, свою очередь, сводится к нахождению таких 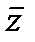 t,
t,  t,
t, 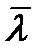 t, удовлетворяющих системе условий (6.28), (6.32), (6.33), которая называется дискретным принципом максимума Понтрягина.
t, удовлетворяющих системе условий (6.28), (6.32), (6.33), которая называется дискретным принципом максимума Понтрягина.
Справедлива теорема.
Теорема 6.2. Совокупность векторов 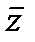 t, t,  t, t, 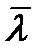 t, удовлетворяющих системе (6.28), (6.32), (6.33), образует седловую точку функции Ф(х, z, λ) (6.30), т. е. при любых допустимых х, z, λ выполняются неравенства t, удовлетворяющих системе (6.28), (6.32), (6.33), образует седловую точку функции Ф(х, z, λ) (6.30), т. е. при любых допустимых х, z, λ выполняются неравенства
|

Доказательство.
Пусть 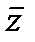 t,
t,  t,
t, 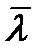 t, удовлетворяют системе (6.28), (6.32), (6.33). Тогда из (6.31) и (6.32) следует, что
t, удовлетворяют системе (6.28), (6.32), (6.33). Тогда из (6.31) и (6.32) следует, что
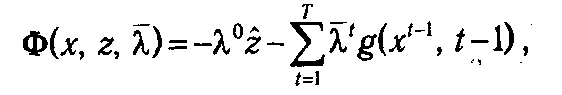
и поскольку  t удовлетворяет (6.33), то
t удовлетворяет (6.33), то
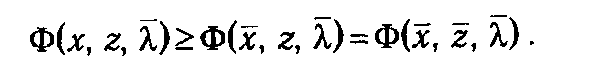
С другой стороны, в силу (6.28) из (6.30) следует, что при любом векторе 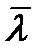 t
t

Следовательно,
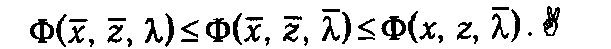
Применяя теорему (6.2), а также положения теории нелинейного программирования, касающиеся связи между решением экстремальной задачи и существованием седловой точки (см. п. 2.2.2), приходим к выводу о том, что векторы 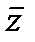 t,
t,  t являются решением простейшей задачи оптимального управления (6.27)-(6.29).
t являются решением простейшей задачи оптимального управления (6.27)-(6.29).
В результате мы получили логически простую схему решения данной задачи: из соотношений (6.32) определяются сопряженные переменные 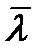 t, затем в ходе решения задачи (6.33) находятся управления
t, затем в ходе решения задачи (6.33) находятся управления  t и далее из (6.28) — оптимальная траектория состояний
t и далее из (6.28) — оптимальная траектория состояний 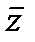 t,.
t,.
Предложенный метод относится к фундаментальным результатам теории оптимального управления и, как уже это упоминалось выше, имеет важное значение для решения многих более сложных задач, которые, так или иначе, сводятся к простейшей. В то же время очевидны и пределы его эффективного использования, которые целиком зависят от возможности решения задачи (6.33).
КЛЮЧЕВЫЕ ПОНЯТИЯ
Ø Ø Игра, игрок, стратегия.
Ø Ø Игры с нулевой суммой.
Ø Ø Матричные игры.
Ø Ø Антагонистические игры.
Ø Ø Принципы максимина и минимакcа.
Ø Ø Седловая точка игры.
Ø Ø Цена игры.
Ø Ø Смешанная стратегия.
Ø Ø Основная теорема матричных игр.
Ø Ø Динамическая транспортная задача.
Ø Ø Простейшая динамическая модель макроэкономики.
Ø Ø Простейшая задача оптимального управления.
Ø Ø Дискретный принцип максимума Понтрягина.
КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Кратко сформулируйте предмет теории игр как научной дисциплины.
6.2. Какой смысл вкладывается в понятие «игра»?
6.3. Для описания каких экономических ситуаций может быть применен аппарат теории игр?
6.4. Какая игра называется антагонистической?
6.5. Чем однозначно определяются матричные игры?
6.6. В чем заключаются принципы максимина и минимакcа?
6.7. При каких условиях можно говорить о том, что игра имеет седловую точку?
6.8. Приведите примеры игр, которые имеют седловую точку и в которых она отсутствует.
6.9. Какие подходы существуют к определению оптимальных стратегий?
6.10. Что называют «ценой игры»?
6.11. Дайте определение понятию «смешанная стратегия».
СПИСОК ЛИТЕРАТУРЫ
1. Абрамов Л. М., Капустин В. Ф. Математическое программирование. Л.,1981.
2. Ашманов С. А. Линейное программирование: Учеб. пособие. М., 1981.
3. Ашманов С. А., Тихонов А. В. Теория оптимизации в задачах и упражнениях. М., 1991.
4. Беллман Р. Динамическое программирование. М., 1960.
5. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. М., 1965.
6. Гавурин М. К., Малоземов В. Н. Экстремальные задачи с линейными ограничениями. Л., 1984.
7. Гасс С. Линейное программирование (методы и приложения). М., 1961.
8. Гейл Д. Теория линейных экономических моделей М., 1963.
9. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация / Пер. с англ. М., 1985.
10. Давыдов Э. Г. Исследование операций: Учеб. пособие для студентов вузов. М., 1990.
11. Данциг Дж. Линейное программирование, его обобщения и применения. М.,1966.
12. Еремин И. И., Астафьев Н. Н. Введение в теорию линейного и выпуклого программирования. М., 1976.
13. Ермольев Ю.М., Ляшко И.И., Михалевич В.С., Тюптя В.И. Математические методы исследования операций: Учеб. пособие для вузов. Киев, 1979.
14. Зайченко Ю. П. Исследование операций, 2-е изд. Киев, 1979.
15. Зангвилл У. И. Нелинейное программирование. Единый подход. М., 1973.
16. Зойтендейк Г. Методы возможных направлений. М., 1963.
17. Карлин С. Математические методы в теории игр, программировании и экономике. М., 1964.
18. Карманов В. Г. Математическое программирование: Учеб. пособие. М., 1986.
19. Корбут А.А., Финкелыитейн Ю. Ю. Дискретное программирование. М., 1968.
20. Кофман А., Анри-Лабордер А. Методы и модели исследования операций. М., 1977.
21. Кюнце Г.П., Крелле В. Нелинейное программирование. М.,1965.
22. Ляшенко И.Н., Карагодова Е.А., Черникова Н.В., Шор Н.3. Линейное и нелинейное программирование. Киев, 1975.
23. Мак-Кинси Дж. Введение в теорию игр. М., 1960.
24. Мухачева Э. А., Рубинштейн Г. Ш. Математическое программирование. Новосибирск, 1977.
25. Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. М, 1970.
26. Оре О. Теория графов. М., 1968.
27. Таха X. Введение в исследование операций/ Пер. с англ. М.,1985.
28. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы последовательной безусловной минимизации. М.,1972.
29. Хедли Дж. Нелинейное и динамическое программирование. М., 1967.
30. Юдин Д.Б., Гольштейн Е.Г. Линейное программирование (теория, методы и приложения). М., 1969.
31. Юдин Д.Б., Гольштейн Е.Г. Линейное программирование. Теория и конечные методы. М., 1963.
32. Lapin L. Quantitative methods for business decisions with cases. Fourth edition. HBJ, 1988.
33. Liitle I.D.C., Murty K.G„ Sweeney D.W., Karel C. An algorithm for traveling for the traveling salesman problem. — Operation Research, 1963, vol.11, No. 6, p. 972-989/ Русск. пер.: Литл Дж., Мурти К., Суини Д., Керел К. Алгоритм для решения задачи о коммивояжере. — В кн.: Экономика и математические методы, 1965, т. 1, № 1, с. 94-107.
Содержание
ПРЕДИСЛОВИЕ............................................................................................................................................................................................................ 2
ВВЕДЕНИЕ.................................................................................................................................................................................................................... 3
ГЛАВА 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.......................................................................................................................................... 8
1.1. ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ............................................................................................. 9
1.2. ОСНОВНЫЕ СВОЙСТВА ЗЛП И ЕЕ ПЕРВАЯ ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ........................................................... 11
1.3. БАЗИСНЫЕ РЕШЕНИЯ И ВТОРАЯ ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗЛП..................................................................... 15
1.4. СИМПЛЕКС-МЕТОД........................................................................................................................................................................................ 17
1.5. МОДИФИЦИРОВАННЫЙ СИМПЛЕКС-МЕТОД..................................................................................................................................... 26
1.6. ТЕОРИЯ ДВОЙСТВЕННОСТИ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ....................................................................................... 30
1.7. ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД................................................................................................................................................... 37
КЛЮЧЕВЫЕ ПОНЯТИЯ.......................................................................................................................................................................................... 42
КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................................................................... 43
ГЛАВА 2. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ................................................................................................................................. 44
2.1. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ...................................................................................... 44
2.2. ДВОЙСТВЕННОСТЬ В НЕЛИНЕЙНОМ ПРОГРАММИРОВАНИИ................................................................................................... 55
КЛЮЧЕВЫЕ ПОНЯТИЯ.......................................................................................................................................................................................... 59
КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................................................................... 59
ГЛАВА 3. ТРАНСПОРТНЫЕ И СЕТЕВЫЕ ЗАДАЧИ................................................................................................................................ 60
3.1. ТРАНСПОРТНАЯ ЗАДАЧА И МЕТОДЫ ЕЕ РЕШЕНИЯ........................................................................................................................ 60
3.2. СЕТЕВЫЕ ЗАДАЧИ........................................................................................................................................................................................... 66
КЛЮЧЕВЫЕ ПОНЯТИЯ.......................................................................................................................................................................................... 73
КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................................................................... 73
ГЛАВА 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ................................................................................................................................... 74
4.1. ТИПЫ ЗАДАЧ ДИСКРЕТНОГО ПРОГРАММИРОВАНИЯ..................................................................................................................... 74
4.2. МЕТОД ГОМОРИ............................................................................................................................................................................................... 78
4.3. МЕТОД ВЕТВЕЙ И ГРАНИЦ.......................................................................................................................................................................... 81
КЛЮЧЕВЫЕ ПОНЯТИЯ.......................................................................................................................................................................................... 86
КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................................................................... 86
ГЛАВА 5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ........................................................................................................................... 86
5.1. ОБЩАЯ СХЕМА МЕТОДОВ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ................................................................................. 86
5.2. ПРИМЕРЫ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ.................................................................................................... 93
КЛЮЧЕВЫЕ ПОНЯТИЯ........................................................................................................................................................................................ 101
КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................................................................ 101
ГЛАВА 6. КРАТКИЙ ОБЗОР ДРУГИХ РАЗДЕЛОВ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ................................................................. 101
6.1. ТЕОРИЯ ИГР...................................................................................................................................................................................................... 101
6.2. ТЕОРИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ........................................................................................................................................... 108
КЛЮЧЕВЫЕ ПОНЯТИЯ........................................................................................................................................................................................ 112
КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................................................................ 112
СПИСОК ЛИТЕРАТУРЫ........................................................................................................................................................................................ 112
 2018-01-08
2018-01-08 3986
3986