Алгоритм граничного перебора по вогнутому множеству. Данный алгоритм основан на генерации подмножеств и их целенаправленном отборе

 

Данный алгоритм основан на генерации подмножеств и их целенаправленном отборе.

Алгоритм генерации подмножеств должен гарантировать, что при его последовательном применении можно построить, начиная с некоторого начального подмножества, все возможные подмножества; при этом не должно быть повторений и должен существовать критерий окончания перебора. В п.2.2 упорядочение перебора произведено сначала по числу i элементов, а затем для фиксированного i – по лексикографическому правилу относительно номеров подмножеств.

Более удобный для дальнейшего упрощения процесса решения алгоритм полного перебора заключается в следующем: сначала строятся все подмножества D_i, содержащие , затем - содержащие , но не содержащие ; если построено подмножество D_i, то за ним строится подмножество D_i+j, целиком содержащее D_i (D_i Ì D_i+j).

Во многих приложениях достаточно находить только безызбыточные покрытия (теорема 2.1), что естественным образом сокращает перебор. Однако не удаётся найти простой и эффективный алгоритм, не требующий построения всех избыточных покрытий. Идея улучшения алгоритма перебора (генерации) подмножеств заключается в следующем: если текущее подмножество - покрытие, то в это подмножество не нужно вводить новые элементы.

Теорема 2.2. Если P покрытие, то и P’, P’ Ê P, тоже покрытие, т.е. множество всех возможных покрытий вогнуто.

Безызбыточные покрытия – это граница вогнутого множества всех покрытий, поэтому модифицированный алгоритм носит название “Алгоритм граничного перебора по вогнутому множеству”.

Словесное описание алгоритма:

0. Текущее подмножество D ={ A₁ }, i=0. Выполняем п.4;

1. Находим наибольший номер j элемента в подмножестве D.

1.1. Если j ¹ n и – не покрытие, то выполняем п.3.

1.2. Если j ¹ n и – покрытие, то выполняем п.2.

1.3. Если j = n, то удаляем из , и если 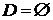, то выполняем п. 5, иначе – снова находим наибольший номер j элемента в D и выполняем п.2.

2. Удаляем элемент из .

3. j=j+1. Вводим элемент в D.

4. Выясняем, является ли покрытием.

4.1.Если очередное построение в – покрытие, то удаляем по очереди из ранее построенных покрытий те, которые поглощают , т.е. избыточные покрытия, соответственно уменьшая i каждый раз на 1, и запоминаем D как покрытие Переходим к п.1;

4.2. Если построение в D не является покрытием, то выполняем п.1;

5. Заканчиваем построение всех безызбыточных покрытий.

Из полученных безызбыточных покрытий можно выбрать покрытия с минимальным количеством строк (кратчайшее покрытие) либо покрытие с минимальной ценой (минимальной покрытие) в соответствии с (2.2).

2.4. Алгоритмы, использующие сокращение таблицы покрытий

Теорема 2.3. (о ядре). Если в столбце таблицы покрытий содержится единственная единица, то строка, содержащая эту единицу, входит во все покрытия и называется ядерной.

Множество ядерных строк заранее выделяется и запоминается для введения во все покрытия. Ядерные строки из ТП удаляются и вычеркиваются все покрытые ими столбцы, т.е. вычеркиваются все столбцы, в которых есть 1 в ядерных строках.

Теорема 1.4. (о б антиядре). Если после удаления ядерных строк и покрытых ими столбцов в какой-либо строке не останется 1, то этa строка не входит ни в одно безызбыточное покрытие. Такие строки называются антиядерными и вычеркиваются из ТП без запоминания.

Определение 2.4. Вектор поглощает вектор , E ³ F, если для всех компонент этих векторов можно одновременно записать . В противном случае векторы называются несравнимимы.

Пример 2.2. Пусть заданы два вектора E=(1,1,0,1), F=(0,1,0,1). Сравнивая их поэлементно (например, слева направо), заключаем, что E ³ F.

Теорема 2.5 (о поглощающих столбцах). В ТП могут быть вычеркнуты все поглощающие столбцы (рассматриваемые как векторы) без ущерба для построения всех безызбыточных покрытий.

Теорема 2.6 (о поглощаемых строках при поиске одного кратчайшего покрытия). Если при решении задачи о покрытии достаточно гарантировать получение хотя бы одного кратчайшего покрытия, то можно удалить все поглощаемые строки.

Теорема 2.7 (о поглощающих строках при построении минимальных покрытий). Если при решении задачи о покрытии достаточно гарантировать построение всех (хотя бы одного) минимального покрытия, то можно вычеркивать поглощаемую строку, если цена её больше или равна цене поглощающей строки.

Используя теоремы 2.3 - 2.7, упрощаем ТП. При этом возможны два исхода.

1. ТП после упрощения становится пустой (вычеркнуты все столбцы). В этом случае множество ядерных строк - требуемое покрытие.

2. Остаток ТП более не упрощается приёмами из теорем 2.3 - 2.7. Получаем циклический остаток (ЦО) таблицы покрытий. Покрытие ЦО таблицы можно строить методами граничного перебора либо разложения по столбцу.

Полное решение (покрытие исходной таблицы) состоит из ядерных строк и строк покрытия ЦО.

Расмотрим варианты алгоритма построения ЦО для ТП.